În [2] nu ne-a reușit să găsim un ciclu hamiltonian al grafului poliedrului hexecontahedral G și ne-am amintit deja de [3] – de unde și reluăm acum, cu unele simplificări (adică, ne-am amintit că în modul cel mai obișnuit folosim nu igraph, ci "backtracking").

Backtraking pentru un ciclu hamiltonian

Modelăm întâi (cât mai simplu) un graf neorientat; constructorul va aloca spațiu pentru vectorul adiacenților fiecărui vârf; adăugăm două metode, pentru înregistrarea și verificarea muchiilor; asigurăm și claselor derivate, posibilitatea de a viza adiacenții fiecărui vârf:

/**  graph.h  **/
#include <vector>
typedef std::vector<int> Bin; // "dulap" pentru adiacenţii unui vârf
class Graph { // graf neorientat (cu vârfurile 0..V-1)
    public:
        Graph(int V): V(V), adj(new Bin[V]) {}  // Constructorul de obiecte
        ~Graph() { delete [] adj; }  // Destructor
        bool isEdge(int, int); // testează existenţa muchiei
        void addEdge(int, int); // adaugă muchie, dacă nu există
    protected: // Clasele derivate vor putea accesa V și adj
        int V;    // numărul de vârfuri
        Bin *adj; // adj[w] = lista adiacenţilor lui w (w=0..V-1)
};

/**  graph.cpp  **/
#include "graph.h"
#include <algorithm>  // find()
void Graph::addEdge(int v, int w) {
    if(! isEdge(v,w)) {
        adj[v].push_back(w);
        adj[w].push_back(v);
    }
}
bool Graph::isEdge(int v, int w) {
    return find( begin(adj[v]), end(adj[v]), w )  != end(adj[v]);
}  // Amintim că end() referă după ultimul element

Un graf hamiltonian este un obiect Graph prevăzut cu o metodă find_path() și un vector în care să se înregistreze ordinea în ciclul hamiltonian, a vârfurilor:

/**  hamilton.h  **/
#include "graph.h"
class Hamilton: public Graph {
    public:
        Hamilton(int n): Graph(n), path(n, 0) {}
        void find_path(int start, bool done = false) { 
            this->done = done;
            find_path(start, 1); // găseşte soluţii, plecând din nodul `start`
        }
        virtual void dump_path(bool); // redă traseul găsit
    protected:
        Bin path; // ordinea pe traseu a vârfurilor (1..V)
    private:
        bool done;  // TRUE după ce se găsește prima soluție (nu vrem alta)
        int start(int); // returnează vârful v găsit la adâncimea path[v]
        void find_path(int, int); // caută recursiv, un ciclu hamiltonian
};

Am renunțat, față de [3], la posibilitatea de a depista un drum hamiltonian – ne interesează ciclurile și anume, unul singur (pe care-l vom semnala prin „flag”-ul done).
Metoda dump_path() va reda soluţia obţinută şi am prevăzut-o virtual, asigurând claselor derivate posibilitatea de a o reformula – având acces la vectorul path (prevăzut prin protected) în care este constituită soluţia.
Metoda exportată find_path(start) lansează de fapt find_path(start, 1) (declarată private) – fixând „adâncimea” 1 pentru nodul start din care va demara căutarea ciclului hamiltonian.
Fiindcă în graful G avem numai 5 vârfuri de grad 5, iar celelalte au gradul 3 (deci listele de adiacență sunt scurte) – am renunțat față de [3], la metoda reorder() (prin care se favorizau pe parcursul căutării, adiacenții nevizitați care au cel mai mic număr de adiacenți nevizitați).
În [3] foloseam start() doar pentru a identifica nodul de start; acum start(d) identifică nodul găsit la adâncimea d (ceea ce este util în dump_path()).

/**  hamilton.cpp  **/
#include "hamilton.h"
#include <iostream>
#include <algorithm>
int Hamilton::start(int depth) {
    return (find( begin(path), end(path), depth )  - begin(path));
}  // identifică nodul găsit la adâncimea dată
void Hamilton::find_path(int node, int depth) { // nodul şi adâncimea curente
    path[node] = depth;  // Căutarea ajunge în node la pasul depth
    if(depth == V && isEdge(node, start(1))) {  // avem un ciclu hamiltonian
        done = true;
        dump_path(true);
    }
    if(! done) {  // avansează sau reia căutarea, după caz
        for(auto next: adj[node])
            if(! path[next])
                find_path(next, depth + 1); // mecanismul backtracking
        path[node] = 0; // revine, pentru a încerca altă variantă
    }
}
void Hamilton::dump_path(bool cycle) {  // afișează ciclul (în termeni 1..V)
    for(int i=1; i <= V; ++i)
        std::cout << (1 + start(i)) << " ";
    std::cout << (1 + start(1)) << '\n';
}

În programul principal asociem unui graf (despre care știm că este graf hamiltonian) un obiect de tip Hamilton, înzestrat cu o metodă proprie pentru specificarea adiacenței:

/**  poliedru.cpp  **/
#include "hamilton.h"
#include <string>
#include <sstream>
#include <fstream>
#include <iostream>
using namespace std;
class Hexecontahedron: public Hamilton {
    public:
        Hexecontahedron(int n): Hamilton(n) { set_adj(); }
    private:
    void set_adj() {
        ifstream ifs("../1257_adj_list.txt");  // listele de adiacență din [2]
        string line;
        for(int i=1; ifs.good(); ++i) {
            getline(ifs, line);
            istringstream iss(line);
            int j;
            while(iss >> j)
                addEdge(i-1, j-1);
        }
    }
};
int main() {
    Hexecontahedron HX(92);
    HX.find_path(91);  // pleacă din vârful "V92" al grafului G (v. [2])
} 
// g++ --std=c++17 -O2 -o poliedru poliedru.cpp hamilton.cpp graph.cpp

Compilând cum se vede pe ultima linie-comentariu, ne-a rezultat un ciclu hamiltonian al grafului G din [2], în circa un minut și 30 secunde:

vb@Home:~/23ian/GRAPH$ time ./poliedru
92 70 13 54 71 14 55 65 18 39 79 17 40 47 5 26 46 4 25 41 3 23 28 1 21 81 24 37 84 38 53 87 52 59 88 60 12 63 58 19 35 57 8 31 56 7 30 51 6 29 36 2 22 82 27 33 83 32 43 20 34 80 89 61 45 11 62 78 91 76 44 85 42 49 10 69 50 86 48 66 9 75 68 90 67 73 16 77 74 15 64 72 92
real 1m27,487s   # (90 secunde – onorabil pentru "backtracking")

Dar cu HX.find_path(0) – adică plecând nu din "V92", ci din nodul "V1" al lui G, sau dintr-un alt vârf afară de "V92" – timpul necesar găsirii ciclului devine mult mai lung…

Este importantă, alegerea nodului din care demarăm căutarea pas cu pas (folosind "backtracking") a unui ciclu hamiltonian. Dacă plecăm dintr-un nod cu puțini adiacenți, atunci (nodul final trebuind să fie unul dintre adiacenții nodului inițial) posibilitățile de a încheia ciclul sunt mai puține, decât în cazul când am pleca dintr-un nod cu mulți adiacenți.
Prin urmare pare firesc să indicăm ca start unul dintre nodurile de grad 5 ale lui G ("V81".."V92", devenite 80..91 în C++), iar nu vreunul dintre celelalte (de grad 3). Este important apoi, care dintre cele 12 noduri de grad 5 este ales drept start; probabil că ordinea în care au fost înscriși adiacenții fiecărui vârf în fișierul "1257_adj_list.txt" favorizează "V92", față de celelalte de gradul 5 (nu mai disecăm rezultatele experimentelor).

Izomorfism, pentru un ciclu hamiltonian

În [2], find_cycles(G, 5) ne-a dat toate ciclurile de lungime 5 ale lui G – dar încercarea de a obține tot așa, un ciclu hamiltonian (fixând 92 în loc de 5) a eșuat; explicația ar fi că funcția igraph::subgraph_isomorphisms() pe care ne-am bazat, produce toate ciclurile respective – devenind impracticabilă pentru cicluri lungi.

Totuși, firesc ar fi să se prevadă și furnizarea unui singur ciclu, dacă lungimea acestuia este mare; oarecum contrariat, m-am uitat până la urmă chiar pe fișierele pachetului igraph – accesându-le pe Github (cum sugerează https://igraph.org/).
În fișierul "topology.R" am identificat funcția graph.subisomorphic.lad() care are și un parametru map prin care se poate forța furnizarea unuia singur, dintre subgrafurile lui G care sunt izomorfe unui graf dat (în cazul nostru, unui graf ciclic). Desigur, m-a surprins constatarea ulterioară că help() (din consola R, pentru funcția respectivă) produce (deocamdată…) tot documentația pentru subgraph_isomorphic() (fără a explicita parametrul "map").

Cu toate acestea (ignorând temerea că „deocamdată nu este disponibilă”), am încercat:

A <- read.table("../graph_1257.mat", sep=" ") %>% as.matrix()
G <- graph_from_adjacency_matrix(A, mode="undirected")
CH <- graph.subisomorphic.lad(make_ring(92), G)
print(CH$map %>% as.vector)
 [1]  1 28 83 32 43 20 34 80 19 35 57 88 58 63 89 61 45 11 62 78 15 64 72 12 60
[26] 70 92 74 77 91 76 44 85 42 49 10 69 50  9 75 68 16 73 67 14 71 54 13 59 52
[51] 87 55 65 90 66 48 86 47 40 17 79 39 18 53 38 84 37  5 26 46  4 25 41  3 23
[76] 81 24  2 36 29  6 51 30  7 56 31  8 33 27 82 22 21  # 1

Funcționează! (deși deocamdată se pare că nu este documentată…)
Am obținut un ciclu hamiltonian diferit (cum de poate constata ușor) de cel rezultat prin "backtracking"; iar de data aceasta (spre deosebire de cazul programului C++ de mai sus) ciclul respectiv a fost produs într-o fracțiune de secundă.
Desigur, pentru a înțelege cum de funcționează așa de rapid, trebuie consultate unele dintre articolele referite în fișierul "topology.R"…

Problema de a identifica subgrafurile izomorfe unuia dat ca șablon, constă în a găsi o funcție injectivă care păstrează adiacența, între mulțimea vârfurilor grafului șablon și mulțimea mai largă a vârfurilor grafului nostru.
graph.subisomorphic.lad() modelează LAD – Logical Analysis of Data; în principiu, se colecteză cât mai multe „potriviri” între datele respective, restrângând apoi prin anumite filtre logice (euristici All-Different Arc Consistency) la un set neredundant specific – ajungând la o clasificare a datelor, după cum satisfac sau nu anumite criterii, sau invarianți; de exemplu, pentru fiecare nod u din graful șablon, se verifică dacă în graful mare există măcar un nod v astfel încât gradele adiacenților lui u să fie cel mult egale, cu gradele adiacenților lui v (altfel corespondența între u și v este „inconsistentă”); sau pentru altă idee, numărul de drumuri de lungime 2 sau 3 între două noduri din graful șablon să fie cel mult egal, cu cel care ar corespunde celor două noduri, în graful mare.
Prin asemenea verificări, gama inițială a potrivirilor se restrânge la acelea care sunt „consistente” și în general, acestea sunt suficiente pentru a desprinde ciclul hamiltonian (și se evită pierderea de timp implicată de revenirile specifice mecanismului "backtracking").

Exercițiu: o încercare manuală, de reprezentare planară

Ne-a rămas să găsim o reprezentare planară a grafului hexecontahedral G.

Ar fi de încercat întâi (probabil, manual) o idee foarte simplă: așezăm pe un cerc (suficient de mare) cele 92 de vârfuri, respectând ordinea acestora în ciclul hamiltonian determinat mai sus; apoi trasăm în interiorul cercului, celelalte muchii (segmentele respective unesc câte două vârfuri ale ciclului hamiltonian și în general, se intersectează între ele).
Apoi, dintre segmentele apărute în interiorul cercului care se intersectează între ele, păstrăm câte unul, iar pe celelalte care îl intersectează pe cel păstrat le „scoatem” în exteriorul cercului – înlocuind „segment” cu câte un arc de curbă trasat în exterior (astfel încât să nu se intersecteze cu arcele deja trasate).

Deocamdată exemplificăm acest procedeu pe un graf mai mic:

adj_lst <- list(
    c(2, 3, 4, 5), c(1, 3, 7, 11), c(1, 2, 9, 12), c(1, 5, 8, 12),
    c(1, 4, 10, 11), c(7, 8, 9, 10), c(2, 6, 9, 11), c(4, 6, 10, 12),
    c(3, 6, 7, 12), c(5, 6, 8, 11), c(2, 5, 7, 10), c(3, 4, 8, 9)
)  # Graph 1024, Name: Cuboctahedral Graph  (https://houseofgraphs.org/)
H <- graph_from_adj_list(adj_lst, mode="all")
CH <- graph.subisomorphic.lad(make_ring(12), H)$map %>% as.vector()
CH <- c(CH, CH[1])   #  1  5  11  7  9  6  10  8  4  12  3  2  1
E(H, path = CH)$color <- "red"  # marchează ciclul hamiltonian
plot(H)

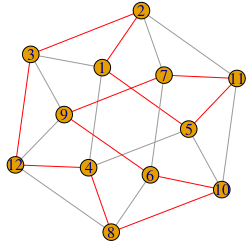
Acest graf corespunde poliedrului Cuboctahedron, cu 8 fețe triunghiuri echilaterale (pe graf: 1-2-3, 1-4-5, etc.) și 6 fețe pătrate (2-3-9-7, etc.); este graf hamiltonian (am obținut în CH un ciclu hamiltonian – marcat cu roșu) și este planar.

Să reținem într-o matrice 'Oth', muchiile din afara ciclului hamiltonian:

df_ch <- setdiff(E(H), E(H, path = CH))
Oth <- ends(H, E(H)[df_ch], names=FALSE)  # muchiile din afara ciclului hamiltonian
              [,1] [,2]              [,1] [,2]
         [1,]    1    3         [7,]    5   10
         [2,]    1    4         [8,]    6    7
         [3,]    2    7         [9,]    6    8
         [4,]    2   11        [10,]    8   12
         [5,]    3    9        [11,]    9   12
         [6,]    4    5        [12,]   10   11

Asociem nodurilor grafului H, în ordinea lor din ciclul hamiltonian găsit mai sus, coordonatele vârfurilor unui dodecagon regulat centrat în origine (plasăm nodul 1 în punctul (1,0) și rotim cu câte 30 de grade, în sens antiorar); apoi plotăm și marcăm nodurile:

fi <- 2*pi/12
coord_z <- exp(1i*seq(0, 2*pi-fi, by = fi)) %>% setNames(CH[1:12])
coord_xy <- data.frame(x = Re(coord_z), y = Im(coord_z)) %>% as.matrix()
plot(c(coord_z, coord_z[1]), type="l", col="gray60")
text(coord_z, label = names(coord_z), col="red")

Avem de adăugat muchiile înregistrate în Oth și ulterior, de hotărât locul fiecăreia – în interior ca segmente, sau în exterior ca arce de curbă; în acest scop este util să constituim un tabel de coordonate pentru capetele celor 12 muchii din Oth:

df <- map_dfr(1:12, function(i) {
    v1 <- as.character(Oth[i, 1]);  v2 <- as.character(Oth[i, 2])
    data.frame(x1 = coord_xy[v1, 1], y1 = coord_xy[v1, 2],
               x2 = coord_xy[v2, 1], y2 = coord_xy[v2, 2], 
               edg = paste0(v1,"-",v2)
    )
})
                   x1            y1            x2            y2   edg
        1   1.0000000  0.000000e+00  5.000000e-01 -8.660254e-01   1-3
        2   1.0000000  0.000000e+00 -5.000000e-01 -8.660254e-01   1-4
        3   0.8660254 -5.000000e-01  6.123234e-17  1.000000e+00   2-7
        4   0.8660254 -5.000000e-01  5.000000e-01  8.660254e-01  2-11
       # ETC.
segments(df$x1, df$y1, df$x2, df$y2, col="gray75")

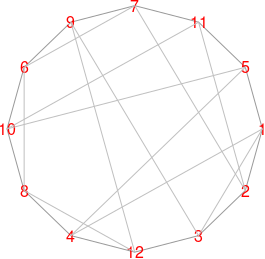
În stânga am redat noua formă a grafului H, cu vârfurile plasate pe un cerc, în ordinea în care se află în ciclul hamiltonian găsit mai sus; segmentele corespunzătoare unora dintre muchii se intersectează și în câte un punct diferit de capete.
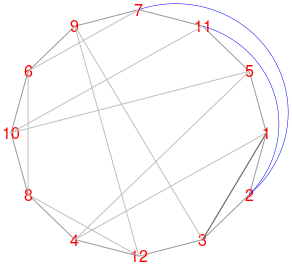
În dreapta imaginii de mai sus, se vede cum am început procesul de planarizare a grafului: am ales pentru început, să păstrăm segmentul care leagă vârfurile 1 și 3; am șters segmentele 2--11 și 2--7 care intersectau segmentul ales 1--3 și în locul lor am trasat (cu "blue") câte un arc de cerc exterior poligonului, între nodurile 2 și 11, respectiv 2 și 7 (cum trasăm aceste arce de cerc este o chestiune deloc banală, dar o omitem aici).

Mai departe: alegem să păstrăm și segmentul 1--4; ștergem cele trei segmente care îl intersectează, 3--9, 12--9 și 12--8 și trasăm în loc arce de cerc exterioare poligonului, între capetele respective (având grijă ca noile arce să nu se intersecteze cu cele deja trasate).

Păstrăm segmentele 5--10 și 11--10, ștergând (și înlocuind cu arc de cerc) segmentul 6--8; în final, obținem această reprezentare planară a lui H:

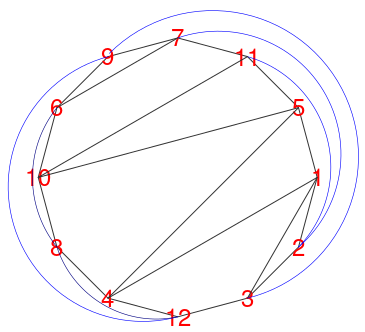
Trebuie să fim de acord că reprezentarea ne-planară inițială este mai instructivă… Totuși, o reprezentare planară precum cea redată mai sus are sens în anumite contexte; de exemplu, dacă nodurile corespund unor circuite electronice, iar pinii unora trebuie legați pe placa respectivă la pinii altora, fără a produce vreun „scurcircuit”.

Este evidentă (și… mai ușor de implementat) o a doua posibilitate de reprezentare planară: așezăm cele 12 noduri, în ordinea lor din ciclul hamiltonian, nu ca mai sus, pe un cerc, ci pe o dreaptă; reprezentăm segmentele interne poligonului prin arce de cerc trasate deasupra dreptei, iar arcele externe poligonului prin arce de cerc trasate dedesubtul dreptei.

Metoda de planarizare arătată mai sus este aplicabilă oricărui graf hamiltonian – dar este greu (sau incomod) de instrumentat dacă graful are prea multe vârfuri și muchii.
În cazul grafului H (cu 92 de vârfuri și 150 de muchii) – probabil că putem doar să ne jucăm: etichetăm 92 de jetoane (dintr-un pachet pentru jocul de Go, de exemplu) cu 1..92, le așezăm în ordinea ciclului hamiltonian pe o „dreaptă” (sau… stradă), distanțându-le între ele măcar cu vreo 15 centimetri și legăm câte două vârfuri care sunt adiacente în H, prin bucăți de sfoară care leagă jetoanele corespunzătoare – rămânând să mutăm unele bucăți de sfoară dintr-o parte a dreptei (deasupra), în cealaltă parte (și scurtând eventual, unele bucăți de sfoară – încât să evităm suprapunerea una peste alta a acestora)… Probabil că scena rezultată ar stârni multe "like"-uri, dacă o vom posta pe vreo rețea de socializare (dar semnificația inițială de "hexecontahedron" se cam pierde).

Pentru cazul lui H, rămâne să ignorăm calitatea de graf hamiltonian și să instrumentăm unul dintre algoritmii „clasici” de reprezentare planară a grafurilor…