O reprezentare planară aerisită

Anterior am obținut o reprezentare convexă „clasică”, a grafului poliedral G: am fixat nodurile unui ciclu în vârfurile unui poligon convex și am plasat celelalte noduri astfel încât fiecare să devină baricentrul adiacenților săi. Apoi am implicat și distanțele dintre nodurile grafului, obținând o reprezentare planară mai „aerisită”; dar așa, vârfurile nu mai sunt baricentre, încât este de văzut dacă reprezentarea respectivă este și ea, una convexă…

Totuși, chiar aerisirea este ceea ce ne interesează; putem îmbunătăți lizibilitatea redării modificând mai departe, calculul coordonatelor și eventual, mutând în final unele puncte (sperând măcar, că nu stricăm convexitatea):

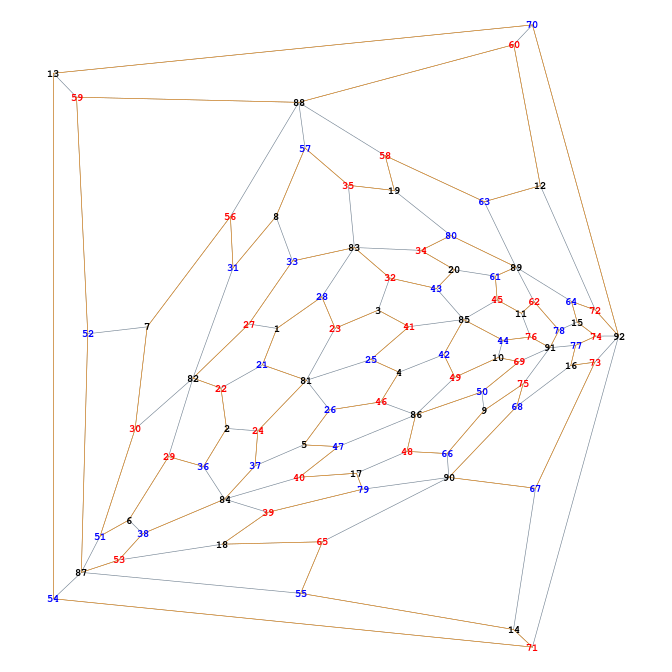
Se poate recunoaște că reprezentarea obținută este încă, una convexă – parcă mai „aerisită” decât cele anterioare, dar nu fără defect: ca urmare a mutării din pozițiile „sigure” (de baricentru), apare acum ici și colo, o senzație de coliniaritate (de exemplu, 29--82--31).
Recuperând colorarea găsită în [2] - I, am evidențiat și faptul că G este graf 3-colorabil: sunt 32 de vârfuri "black", 30 "blue" și 30 "red" (iar cele adiacente au culori distincte).

Pentru calculul matricei Q (v. [2] - V) am folosit acum:

Q <- A  # vom pondera adiacențele existente
dil <- -1.75  # un coeficient de "dilatare" (din experimente: -1; -0.25; -0.5; etc.)
for(i in 1:91) 
    for(j in (i+1):92)
        if(Q[i, j] > 0 & !(i <= 5 & j <= 5)) {
            di <- Dmin[as.character(CH[i])]  # distanța nodului la ciclul de bază
            dj <- Dmin[as.character(CH[j])]
            Q[j, i] <- Q[i, j] <- max(di, dj)^dil / (di + dj)
        }                      # în [2] aveam doar 1/max(di, dj)

iar înainte de a trece la plotare, am modificat afixele unora dintre puncte, cam așa:

aZ["73"] <- aZ["73"] + 4 - 4i  # deplasează puțin punctul asociat nodului "73"
aZ["72"] <- aZ["72"] + 4 + 4i
aZ["64"] <- aZ["64"] + 5i

Bineînțeles că în prealabil, am determinat – de data aceasta, corect (și nu prin încercări) – valorile de încadrare a graficului, xlim și ylim:

plot(0, type = "n", xlim = range(Re(aZ)), ylim = range(Im(aZ)), asp=1)

Desigur, investigația pe care am desfășurat-o în [2] (I..VI) asupra grafului hexecontaedral G a implicat și consultarea în diverse locuri, a unor rezultate și construcții memorabile:
— teorema lui Ernst Steinitz, 1922: orice graf planar triconex este scheletul unui poliedru convex;
— teorema lui Karl Menger, 1927: un graf este n-conex <=> între oricare două vârfuri există n căi independente (și în orice graf n-conex, oricare n vârfuri se află pe câte un același ciclu);
— teorema lui Tutte, 1963: orice graf planar triconex are o reprezentare planară convexă, care se poate găsi ca poziția de echilibru a unui sistem de arce materiale extensibile asociate muchiilor (presupunând fixată una dintre fețe);
— teorema lui Herbert Grötzsch, 1959: orice graf planar care nu conține triunghiuri este 3-colorabil (și orice graf planar care nu are cicluri de lungimi 4..7 este 3-colorabil);
— orice graf planar care are un ciclu hamiltonian, admite o reprezentare de tip "2-book".

În [2] am verificat că G are 5-cicluri, dar nu are cicluri de lungimi 3, 4, 6 și 7; am găsit totuși o 3-colorare (uniformă) și am găsit un ciclu hamiltonian CH (marcat prin "darkorange", mai sus), ajungând și la reprezentări de tip "n-book" (deasemenea, la reprezentări convexe lizibile).
Subliniem că am ajuns să ne ocupăm de graful hexecontaedral G plecând de la probleme ridicate de construcția orarului școlar – de aceea am păstrat ca referință, [1].