Pentru o "bază" a ciclurilor unui graf, de care adusesem vorba în [1], se poate pleca de la un arbore de acoperire al grafului: mulțimea ciclurilor care se formează de fiecare dată când adăugăm arborelui un arc dintre cele rămase în afara lui, constituie un "set de cicluri fundamentale". Lucrurile depind totuși de ce vrem prin "graf" (neorientat, digraf; conex, tare-conex ?) și de ce înseamnă "cicluri" (ciclu, "semiciclu", și una și alta, circuit, semicircuit ?)…

În automatul mod M stările 0:(M-1) reprezintă numerele naturale modulo M, iar tranzițiile sunt date de regula $t=2s+(0\,sau\, 1)\,\,(\mathrm{mod}\,$ M). Pentru a explora/expune mai ușor, alegem cazul (diferit totuși de cele întâlnite în [1]) M = 9:

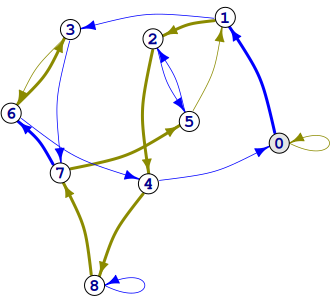
Arcele îngroșate formează un arbore acoperitor:

Am dedus $H_1$ din circuitul eulerian următor, reținând pentru fiecare vârf numai prima dintre aparițiile acestuia:

> eulerian_cycle(Atm)$vpath %>% attr("names") %>% as.integer()
     [1] 0 0 1 2 4 8 8 7 6 3 7 5 2 5 1 3 6 4 0

Obs. Prin complementare față de $(M-1)$ (v. [1]-IV), din $H_1$ rezultă un al doilea arbore acoperitor — dar datorită complementarierii, aceștia sunt "echivalenți" în privința proprietăților pe care le-am stabili plecând de la unul, respectiv de la celălalt. Altfel spus… dacă ar fi să vizăm toți arborii acoperitori, probabil că ar fi suficient să considerăm numai jumătate dintre ei.

În afara arborelui $H_1$ au rămas 8 arce (ignorăm de regulă, buclele $0-0$ și $8-8$); oricare dintre acestea formează împreună cu arce existente în $H_1$, un ciclu (sau… un semiciclu). Ciclurile rezultate astfel diferă între ele măcar prin muchia adăugată arborelui (deci nu se poate deduce unul din celelalte, adică cele 8 cicluri formate astfel sunt independente între ele).

De exemplu, adăugând în $H_1$ arcul $4-0$ rezultă circuitul $4-\boldsymbol{0-1-2-4}$; dacă în $H_1$ adăugam arcul $5-1$, se închidea circuitul $5-\boldsymbol{1-2-4-8-7-5}$; ș.a.m.d.
Dar… fiindcă din $3$ nu iese nici un arc al lui $H_1$, arcul $1-3$ nu poate forma un circuit, împreună cu arce din $H_1$ — ci doar un "semi-ciclu", în care arcul $1-3$ este inclus cu sens invers: $3\leftarrow 1\rightarrow\boldsymbol{2-4-8-7-6-3}$ (sau… cu altă orientare a ciclului, $1\rightarrow \boldsymbol{3}\leftarrow 2\leftarrow 4\leftarrow 8\leftarrow 7\leftarrow 6\rightarrow \boldsymbol{3}$).

Prin urmare, $H_1$ ne-ar conduce la un set de "cicluri fundamentale" pentru graful neorientat subiacent digrafului Atm. Am vrea noi… un set de circuite (păstrând direcționalitatea arcelor) — având în vedere motivul introdus în [1], de a formula o expresie regulată pentru formele binare ale multiplilor de M (alipind formei binare a unui număr aflat în starea $s$, biții de pe arcele unui circuit care pleacă din $s$, obținem forma binară a unui număr congruent mod M celui din starea $s$); dar se pare că nu vom putea obține așa ceva: orice arbore acoperitor am folosi în loc de $H_1$, în setul de "cicluri fundamentale" asociat lui vom găsi mereu câte măcar un "semiciclu"…

Obs. Funcția nx.number_of_spanning_trees() din pachetul networkx ne arată că avem 189 de arbori acoperitori (sau arborescențe) și îi putem obține prin nx.ArborescenceIterator(); ar trebui să observăm că dacă fixăm vârful-rădăcină al arborelui, ar rezulta 189 / 9 = 21 de arbori cu o aceeași rădăcină și n-am avea decât să iterăm pe fiecare, construcția setului de "cicluri fundamentale", până ce am găsi poate, unul care să producă circuite (nu și vreun "semi-ciclu")… Ar fi și mai simplu, dacă am putea folosi funcția nx.cycle_basis() — dar acum, aceasta este implementată numai pentru grafuri neorientate (altfel — aplicând-o pe nx.to_undirected(Atm) — rezultă de regulă "semicicluri").

Ciclurile grafului neorientat subiacent digrafului

Pentru M=9, graful neorientat subiacent digrafului redat mai sus poate arăta așa:

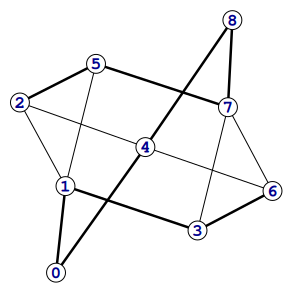
Am redus arcele duble $6-3-6$ și $2-5-2$ la câte o singură muchie — cu această motivare: un circuit de lungime 2 nu se poate exprima prin cicluri mai scurte, deci trebuie să facă parte din oricare bază de cicluri a digrafului (urmând ca în final, să adăugăm arcul dublu respectiv bazei găsite pentru graful neorientat subiacent).

Să desemnăm prin G =(V, E) graful neorientat asociat mai sus, digrafului Atm; G are 9 vârfuri și 14 muchii. Muchiile îngroșate marchează un arbore de acoperire, H (chiar drum hamiltonian al lui G, spre deosebire de $H_1$ specificat mai sus), pe care l-am ales (pentru poza simetrică rezultată) dintr-o sublistă a tuturor arborilor acoperitori:

spann_trees <- function(M) {
    Tree <- make_tree(M, children = 1, mode = "undirected")
    # children = 2 pentru arbori acoperitori care nu sunt căi hamiltoniene
    subgraph_isomorphisms(Tree, G)
}
ST <- spann_trees(9)  # rezultă 54 drumuri hamiltoniene...
H <- ST[[16]]  # sau, pentru unul ales aleatoriu: H <- ST %>% sample(1)
> str(H)  # vârfurile ierarhizate de H și numele acestora din G
 'igraph.vs' Named int [1:9] 3 8 9 7 4 1 2 5 6
 - attr(*, "names")= chr [1:9] "2" "5" "7" "8" "4" "0" "1" "3" "6"

Nu ne vor interesa toți arborii acoperitori, dar subliniem că între cei 54 obținuți în ST (care, fiindcă în make_tree() am folosit children=1, sunt drumuri hamiltoniene), fiecare apare de două ori (după cum citim de la un capăt sau de la celălalt) — având în vedere că fiecare corespunde unui alt izomorfism între 'Tree' și un subgraf al lui G.

Nu este important aici, totuși redăm secvența prin care am plotat (precum în poza așezată mai sus) graful G (sub pachetul igraph):

E(G)$width <- 1  # inițializează grosimea muchiilor lui G
edge_attr(G, "width", 
    index = E(G, path = attr(H, "names"))) <- 2.5  # îngroașă muchiile lui H
coords <- readRDS("coords.RDS")  # reținut din plotări anterioare; layout_nicely()
plot(G, layout = coords,
     vertex.color="white", edge.color="black",
     vertex.label.font=2, vertex.label.family="mono", vertex.label.cex=1.1
)

Subliniem că H nu este decât un 'igraph.vs' — secvență de vârfuri și nume din G, în ordinea parcurgerii drumului hamiltonian respectiv; însă este important să vedem H ca obiect de tip 'igraph' — mai precis, ca subgraf al lui G (încât să putem invoca apoi, funcții specifice grafurilor):

H <- subgraph.edges(G, as_ids(E(G, path = H)))
    IGRAPH 536a97f UN-- 9 8 -- 
    + attr: name (v/c), width (e/n)
    + edges from 536a97f (vertex names):
    [1] 0--1 0--4 1--3 3--6 4--8 2--5 8--7 5--7

Când adăugăm în H o muchie $uv$ din G$\boldsymbol{-}$H, în graful rezultat vom avea două căi între $u$ și $v$: una banală, de lungime 1 (muchia $u-v$) și una care are lungimea mai mare ca 2 și care de fapt este ciclul simplu format în H prin adăugarea muchiei respective; folosind k_shortest_paths(), putem determina ciclul respectiv:

get_cycle <- function(He, euv) {
    P2 <- k_shortest_paths(He, from = euv[1], to = euv[2], 
                           k = 2) $vpaths[[2]]
    Cy <- attr(P2, "names") %>% as.vector()
    c(Cy, Cy[1])  # ciclul format de euv cu muchii din arborele acoperitor
}

Următoarea funcție produce o listă care asociază fiecărei muchii rămase în afara arborelui acoperitor (primit ca parametru), ciclul format în acel arbore prin adăugarea muchiei respective:

get_basis <- function(Spt) {  # "Spanning Tree" al lui G
    base <- list()
    G1 <- G - Spt  # G1 are 6 muchii (deci vor rezulta 6 "cicluri fundamentale")
    for(i in 1:gsize(G1)) {
        uv <- ends(G1, E(G1)[i]) %>% as.vector()
        G2 <- Spt + path(uv)
        base[[paste0(uv[1], '-', uv[2])]] <- get_cycle(G2, uv)
    }
    base  # baza de cicluri ale lui G, asociată arborelui Spt
}

De exemplu, avem:

> FS <- get_basis(H)
> FS $"1-5"  # ciclul format în H prin adăugarea muchiei 1-5
[1] "1" "0" "4" "8" "7" "5" "1"  # sau 1578401

Bineînțeles că dacă am considera un alt arbore acoperitor (în loc de H, ales mai sus numai din considerente estetice), am obține prin get_basis() un alt set de cicluri fundamentale (poate cu un număr total de muchii mai mic — dar nu ne oprim acum, asupra acestui aspect).

Pentru a genera alte cicluri (pe baza ciclurilor fundamentale găsite), formulăm întâi matricea de incidență față de muchiile grafului, a bazei respective:

ord_edg <- c(attr(E(G-H), "vnames"), attr(E(H), "vnames"))
IM <- matrix(0L, nrow=length(FS), ncol=gsize(G), byrow=TRUE,
          dimnames = list(chord = names(FS),
                          edges = ord_edg)
      )
for(i in 1:nrow(IM)) {
    Cy <- FS[[i]]
    for(j in 1:(length(Cy)-1)) {
        col <- paste0(Cy[j], '|', Cy[j+1])
        if(! col %in% colnames(IM))
            col <- paste0(Cy[j+1], '|', Cy[j])
        IM[i, col] <- 1L
    }
}
         edges
    chord 1|5 1|2 2|4 4|6 3|7 6|7 0|1 0|4 1|3 3|6 4|8 2|5 8|7 5|7
      1-5   1   0   0   0   0   0   1   1   0   0   1   0   1   1    1578401
      1-2   0   1   0   0   0   0   1   1   0   0   1   1   1   1    12578401
      2-4   0   0   1   0   0   0   0   0   0   0   1   1   1   1    248752
      4-6   0   0   0   1   0   0   1   1   1   1   0   0   0   0    463104
      3-7   0   0   0   0   1   0   1   1   1   0   1   0   1   0    3784013
      6-7   0   0   0   0   0   1   1   1   1   1   1   0   1   0    67840136

Prin ord_edg am ordonat muchiile lui G astfel încât primele să fie cele din G$-$H, adăugate de fiecare dată lui H; ca urmare, fiindcă liniile corespund ciclurilor din FS (și sunt numite după muchia 'chord' adăugată în H), primele 6 coloane din IM constituie matricea unitate (de ordinul 6; implicit, rangul matricei IM este 6 — adică într-adevăr, cele 6 cicluri înregistrate în IM sunt independente între ele).
La capătul fiecărei linii am consemnat ciclul corespunzător în lista FS (concatenând vârfurile ciclului — fără teamă de confuzii: G are numai 9 vârfuri); valorile 1 de pe o linie marchează muchiile care formează ciclul respectiv (muchiile fiind redate, drept nume de coloane, în notația standard: separând capetele prin '|').

Oricare ciclu al lui G — nu neapărat "elementar", putând fi chiar și reuniune de cicluri disjuncte — se obține din cele 6 cicluri fundamentale, însumând modulo 2 anumite linii ale matricei IM.
Să considerăm de exemplu, ciclul-trapez C = "246312" (care nu figurează în setul FS); în C apar chord-urile $2-4$, $4-6$ și $1-2$, care au determinat ciclurile fundamentale de pe liniile 3, 4 și 2 ale matricei IM — să le notăm aici prin $C_3$, $C_4$ și $C_2$; atunci avem C = $C_2 \oplus C_3 \oplus C_4$, unde '$\oplus$' desemnează adunarea modulo 2 (sau, operația binară "XOR"), prin care se rețin din două cicluri muchiile care apar numai într-unul (iar dacă însumăm mai multe cicluri, muchiile care apar într-un număr impar de operanzi). Avem: $C_2 \oplus C_3 \oplus C_4 = \{1|2,2|4,1|3,3|6\}$ = "124631", care este totuna ca ciclu, cu "246312".
Pentru un alt exemplu, în ciclul C1="0487510" apare un singur "chord": $5|1$ care (fiind vorba de graf neorientat) este totuna cu $1|5$, înregistrat în numele chord al primei linii din IM; deci de fapt, C1 coincide cu ciclul fundamental din prima linie.

În sfârșit, să vedem ce rezultă aplicând '$\oplus$' pe un grup oarecare de linii din IM — de exemplu, să însumăm toate liniile:

column_xor <- function(Col)
    Reduce(bitwXor, as.integer(Col))
sum2_rows <- sapply(1:ncol(IM), function(K) column_xor(IM[, K])) %>% 
             setNames(colnames(IM))
    1|5 1|2 2|4 4|6 3|7 6|7 0|1 0|4 1|3 3|6 4|8 2|5 8|7 5|7 
      1   1   1   1   1   1   1   1   1   0   1   0   1   1

Rezultatul este reuniunea a două cicluri (fără muchii comune): "1246731" și "0157840" (al doilea coincide cu ciclul fundamental din prima linie IM).

Obs. Liniile din IM pot fi interpretate (ușor) ca forme binare de întregi; dar ar fi vorba de "întregi lungi", pentru care nu puteam folosi bitwXor() (în R dispunem numai de "întregi scurți").
Bineînțeles, fiindcă $1\oplus1=0$, puteam formula column_xor() mai simplu: returnează 1 dacă pe coloana respectivă se află un număr impar de valori '1'.

Dacă vrem să însumăm nu toate liniile ca mai sus, ci numai anumite linii — n-avem dacât să aplicăm column_xor() pe submatricea lui IM care conține liniile respective.
Însumând (modulo 2) linii din IM în toate modurile posibile — obținem toate ciclurile grafului neorientat G (și reuniuni de cicluri disjuncte).

Dacă adăugăm în IM și ciclurile de lungime 2 (neglijate în G) $2-5-2$ și $3-6-3$, obținem o bază de cicluri (sau semicicluri) pentru automatul mod 9 din care a provenit graful neorientat G. Să observăm că pentru digraful Atm, ciclul pomenit mai sus Q: "1246731" este un semiciclu (în care numai primele două arce păstrează orientarea existentă în Atm); dar putem găsi un circuit (ne-elementar) în Atm, care să conțină toate muchiile lui Q (dar orientate corect) — de exemplu: "124876487637513751".

Ar fi poate de încercat, dar chiar nu credem că dacă am pleca de la vreun alt arbore acoperitor (în loc de drumul hamiltonian H considerat mai sus), am obține o bază de circuite pentru automatul respectiv…
Există însă acest rezultat, citat (eventual, expediat) în diverse locuri (articole și cărți de teoria grafurilor): "Orice digraf tare-conex admite o bază de circuite"; ne-ar rămâne să încercăm un alt algoritm, în loc de cel prezentat mai sus (care pleacă de la un arbore acoperitor… Oare de la ce altceva, am putea pleca ?).

Orientarea implică totuși, îndoială…

N-am dat de o demonstrație coerentă și pe seama literaturii investigate (sau răsfoite), nu este suficient de clar dacă în rezultatul citat este vorba (cum credeam) de circuite (propriu-zise) ale digrafului, sau totuși, de "semi-circuite" — orientate numai după arcul adăugat arborelui de la care a plecat constituirea bazei (în timp ce orientarea altor arce ale "circuitului fundamental" nu rămâne neapărat, cea reală).
Exemplul de mai sus pentru Q, sugerează în fond că orice semi-circuit (într-un digraf tare-conex) poate fi reexprimat ca un circuit (propriu-zis), deci ar fi suficient să avem o bază de "semi-circuite" (și nu neapărat, de circuite) — încât s-ar putea ca enunțul citat să vizeze de fapt nu circuite (cum credeam), ci doar (dar suficient) semi-circuite.

Ar rămâne de demonstrat că semi-circuitele unui digraf tare-conex pot fi exprimate cumva, ca circuite propriu-zise — ceea ce parcă n-ar fi așa de greu, ținând seama că în fiecare vârf pleacă și intră câte un același număr de arce: când pe semicircuit întâlnim un arc incorect orientat, îl vom putea înlocui printr-un drum corect orientat, care unește capetele acelui arc (cam cum am procedat mai sus față de semiciclul Q).