Chestiunea cuplajelor existente în orarul şcolar (IV)
Cu daySchoolSchedule.R din [2], putem genera foarte rapid orarele zilnice (având repartiţia lecţiilor pe zile), dar fără să ţinem seama de semnificaţia profesorilor fictivi (introduşi în [1] pentru mascarea lecţiilor cuplate); pentru a corecta imediat poziţia cuplajelor, vom folosi deocamdată aplicaţia interactivă "dayRecast.html" (v. /dayRecast şi github). Apoi, vom completa programul "recast.R" din [3], astfel încât reducerea de ferestre din orarul rezultat să ţină seama şi de situaţiile de cuplare.
Generarea orarelor zilnice (ignorând cuplajele)
Cu prilejul acestei noi încercări, începem să reorganizăm lucrurile; întâi, eliminăm din fişierele "daySchoolSchedule.R" şi "recast.R", diversele funcţii utilitare comune (cnt_holes(), get_betweenness(), orarByProf() şi altele) – plasându-le pe toate într-un fişier separat, "stmt_utils.R" (în care am inclus şi library(tidyverse)).
Reformulăm programul din [2], restrângându-l la funcţia mount_hours(), prin care lecţiile prof|cls dintr-o aceeaşi zi vor fi etichetate cu orele 1..7 ale zilei (astfel încât să se evite suprapunerile şi profesorii să nu aibă mai mult de două ferestre):
# daySchoolSchedule.R source("stmt_utils.R") # cnt_holes(), get_betweenness(), orarByProf(), etc. Pore <- readRDS("lstPerm47.RDS") # lista matricelor de permutări 4..7 (ore) nGaps <- 24 # maximum convenit pentru totalul ferestrelor # etichetează cu .$ora, lecţiile prof|cls ale zilei, astfel încât # fiecare profesor are zero, una sau cel mult două ferestre mount_hours <- function(lessons) { btw_prof <- get_betweenness(lessons, 1) %>% sort() btw_cls <- get_betweenness(lessons, 2) %>% sort() task <- lessons %>% mutate(prof = factor(prof, levels = names(btw_prof), ordered=TRUE)) %>% arrange(prof, cls) hBits <- rep(0L, nlevels(task$prof)) # alocările de ore (biţi) la profesori names(hBits) <- levels(task$prof) Z <- task %>% split(.$cls) # desparte lecţiile după clasă lstCls <- names(Z) btw_cls <- btw_cls[lstCls] mountHtoCls <- function(Q) { # alocă pe 1..7, lecţiile unei clase mpr <- Pore[[nrow(Q)-3]] # matricea de permutări corespunzătoare clasei bhp <- bith[Q$prof] # biţii alocaţi anterior, profesorilor clasei for(i in 1:ncol(mpr)) { po <- mpr[, i] bis <- bitwShiftL(1, po - 1) if(any(bitwAnd(bhp, bis) > 0)) next # caută o permutare care să evite biţi '1' alocaţi deja # Dacă un profesor are 2 sau mai multe ore pe zi la aceeaşi clasă if(anyDuplicated(names(bhp)) > 0) { for(jn in 1:(nrow(Q)-1)) { if(names(bhp)[jn] == names(bhp)[jn+1]) bis[jn] <- bis[jn+1] <- bis[jn] + bis[jn+1] } } # (a comenta, dacă NU există profesor cu 2 ore la clasă) blks <- bitwOr(bhp, bis) # cumulează biţii vechilor şi noii alocări Cond1 <- unlist(lapply(blks, cnt_holes)) if(any(Cond1 > 2)) next # controlează numărul de ferestre bith[Q$prof] <<- blks return(Q %>% mutate(ora = po)) # înscrie orarul clasei curente } return(NULL) # pentru clasa curentă NU s-a reuşit un orar "bun" } odf <- vector("list", length(lstCls)) # va înregistra orarele claselor names(odf) <- lstCls while(TRUE) { succ <- TRUE bith <- hBits # reiniţializează octeţii de alocare pe orele zilei lstCls <- sample(lstCls, prob = btw_cls) for(K in lstCls) { W <- mountHtoCls(Z[[K]]) # încearcă un orar pentru clasa curentă if(is.null(W)) { succ <- FALSE break # abandonează ('for') în caz de insucces } odf[[K]] <- W # salvează orarul constituit clasei curente } if(succ) { NG <- sum(unlist(lapply(bith, cnt_holes))) cat(NG, " ") # afişează totuşi, totalul ferestrelor if(NG <= nGaps) break # iese din 'while' (fiind cel mult 'nGaps' ferestre) } } bind_rows(odf) # returnează orarul lecţiilor zilei (prof|cls|ora) }
Pentru a obţine orarele pentru lecţiile repartizate anterior pe zile în fişierele "dis_*.RDS" (unde '*' este "Lu", "Ma", etc.), putem formula acum următorul program:
# 5days.R source("daySchoolSchedule.R") # tidyverse; "stmt_utils.R"; mount_hours() days <- c("Lu", "Ma", "Mi", "Jo", "Vi") orar <- vector("list", 5) names(orar) <- days prnTime() # din "stmt_utils.R" for(zi in days) { lssn <- readRDS(paste0("dis_", zi, ".RDS")) %>% mutate(prof = tolower(sub('-','', prof))) orar[[zi]] <- mount_hours(lssn) prnTime() }
Am ţinut cont aici (prin tolower() şi sub()) că în repartiţia pe zile preluată din [1] aveam notaţii ca "P25" şi "P08-P25", iar ulterior am adoptat notaţia "p08p25".
Orarele se obţin chiar foarte repede (în condiţiile asumate mai sus) – de exemplu:
> source("5days.R") [1] 18:51:51 30 26 27 26 30 29 32 30 29 27 34 31 28 24 [1] 18:51:55 # Lu 26 22 [1] 18:51:56 # Ma (cu 22 ferestre) 30 26 32 30 27 27 27 30 27 25 24 [1] 18:52:02 # Mi 19 [1] 18:52:05 # Jo (cu 19 ferestre) 29 37 24 [1] 18:52:07 # Vi (24 ferestre) > saveRDS(orar, file="orar_lst5_7.RDS")
Pentru ziua "Lu" de exemplu, vedem că s-au generat 13 orare înainte de a ajunge (după :51:55-:51:51 = 4 secunde) la unul cu 24 de ferestre. Desigur, repetând o a doua oară execuţia programului "5days.R", va rezulta un alt set de orare zilnice, cu mai multe sau mai puţine generări de orare intermediare şi cu durate care oscilează între câteva secunde şi două-trei minute.
Ajustarea cuplajelor
Subliniem că în mount_hours() am ignorat lecţiile cuplate, încât orarele rezultate ascund anumite suprapuneri de ore… Considerăm orarul unei zile oarecare şi-l redăm într-o formă convenabilă pentru observarea defectelor privitoare la cuplaje:
source("stmt_utils.R") # orarByProf(), orarByCls(), etc. Z <- readRDS("orar_lst5_7.RDS") lu <- Z[["Lu"]] M <- as.matrix(orarByCls(lu)) print.table(M) cls 1 2 3 4 5 6 7 [1,] 10A p01p02 p36 p12 p14 p13 p21 p15 [2,] 10B p32 p18 p09 p22 p05 p15 [3,] 10C p38 p07 p05 p25 p35 p16 [4,] 10D p31 p12 p16 p09 p21 p19 [5,] 10E p34p07 p28 p46 p39 p03 p27 p04 [6,] 10F p03 p06p33 p45 p11 p20 p35 [7,] 11A p25 p01 p35 p40 p23 p20 [8,] 11B p28 p01p02 p13 p05 p02 p12 [9,] 11C p30 p31 p28 p17 p18 [10,] 11D p27 p10 p04 p02 p58 [11,] 11E p11p44 p26 p10 p03 p09 [12,] 11F p09 p06 p25 p23 p26 p14 [13,] 12A p01 p30 p01p02 p36 p17 p04 [14,] 12B p22 p29 p30 p16 p24 p17 [15,] 12C p29 p23 p42 p18 p19 p07 [16,] 12D p49 p22 p08 p15 p27 [17,] 12E p08p47 p08p25 p19 p21 p15 p08p11 [18,] 12F p12 p20 p06 p04 p07 p26 [19,] 5G p06 p46 p17 p56 p04 p45 [20,] 6G p50 p42 p56 p08 p45 p24 [21,] 7G p62 p24 p21 p32 p40 p33 [22,] 8G p61 p14 p20 p13 p46 p56 p05 [23,] 9A p36 p32 p02 p24 p14 p05 [24,] 9B p11 p03 p31 p10 p16 p22 [25,] 9C p06p33 p37 p11 p07 p10 p03 [26,] 9D p18 p33 p26 p19 p29 p39 [27,] 9E p34p09 p38 p03 p27 p39 p13 [28,] 9F p37 p08 p23 p45 p33 p10
Bineînţeles că în fiecare coloană orară 1..7, fiecare dintre profesori apare cel mult o singură dată (nu există suprapuneri de ore); dar "p01p02" de exemplu, este un profesor fictiv – plasarea lui pe ora întâia la 10A însemnând că pentru desfăşurarea acestei ore, 10A este împărţită în două grupe, la care intră respectiv profesorii („reali”) p01 şi p02; desigur că pentru aceasta, atât p01 cât şi p02 trebuie să fie liberi în ora respectivă – ori vedem că p01 este deja fixat pe ora 1 la clasa 12A.
Pentru un alt exemplu, "p06p33" se suprapune în ora a doua (clasa 10F) şi cu p06 (care are oră la 11F) şi cu p33 (care are oră la 9D). La fel, "p34p07" se suprapune în ora întâia cu "p34p09" (la 10E şi respectiv, 9E).
N-ar fi greu de corectat direct, lucrurile; de exemplu, prin
M[13, c(2, 6)] <- M[13, c(6, 2)]
p01 şi p17 vor schimba între ei poziţiile de pe linia 13 (la clasa 12A) – disponibilizând p01 pentru a face ora I-a împreună cu p02, la 10A; de observat că iniţial, p17 nu apărea în coloana 2 şi deci, mutarea efectuată nu creează vreo nouă suprapunere.
Dar astfel de manipulări directe (probabil numeroase) sunt riscante, neavând pentru suprapuneri alt control decât cel vizual (prin proprii ochi); până vom pune la punct şi o procedură automată pentru ajustarea în orar a lecţiilor cuplate – preferăm să apelăm la aplicaţia interactivă "dayRecast.html" (şi pentru a nu proceda astfel pentru fiecare zi, va fi necesară o procedură „automată”).
Salvăm deocamdată orarul, în formatul CSV agreat de "dayRecast.html":
> write_csv(orarByProf(lu), file="orar_Lu.csv", na="-", col_names=TRUE)
Aranjarea liniilor orarului, pentru a evidenţia cuplajele
Avem de folosit "dayRecast.html" numai pentru a corecta suprapunerile de lecţii cuplate (fără a ne preocupa de ferestre); pentru a opera interactiv cât mai comod (şi rapid), rearanjăm întâi liniile din fişierul CSV rezultat mai sus, astfel încât să grupăm la început toate liniile corespunzătoare profesorilor cuplaţi.
Din [1], avem în "messing.RDS" listele Lx1 şi Lx2, care specifică – pentru întreaga săptămână – pentru fiecare profesor care intră într-un cuplaj şi respectiv, pentru fiecare profesor fictiv, acei profesori şi profesori fictivi de care depinde alocarea corectă (fără suprapuneri) a cuplajelor; mai precizăm că am mutat în "stmt_utils.R" şi funcţia utilitară introdusă în [1], select_cupl(), prin care selectăm din Lx1 şi Lx2 numai datele corespunzătoare zilei curente.
Următorul script produce rearanjarea dorită a liniilor orarului:
# update.R source("stmt_utils.R") # select_cupl(L, prof_day) load("messing.RDS") # Lx1, Lx2 (cuplajele din cadrul săptămânii) X <- read_csv("orar_Lu.csv", col_types = "cccccccc") prof_day <- unique(X$prof) # profesorii (şi cei fictivi) pe ziua curentă Lx1 <- select_cupl(Lx1, prof_day) # ; print(Lx1) Lx2 <- select_cupl(Lx2, prof_day) # ; print(Lx2) # de cine depinde un profesor cuplat sau un cuplu, la alocarea lecţiilor nx1 <- names(Lx1); nx2 <- names(Lx2) dep1 <- unlist(map(seq_along(Lx1), function(i) c(nx1[i], Lx1[[i]]))) dep2 <- unlist(map(seq_along(Lx2), function(i) c(nx2[i], Lx2[[i]]))) # ordonează după cuplaje şi apoi, alfabetic (pentru lizibilitate) dep <- unique(union(dep1, dep2)) lev <- c(dep, sort(unique(setdiff(X$prof, dep)))) X$prof <- factor(X$prof, levels = lev, ordered=TRUE) X <- X %>% arrange(prof) write_csv(X, file="orar_Lu_1.csv", col_names=TRUE)
Transferând fişierul obţinut "orar_Lu_1.csv" în locul cuvenit din fişierul "dayRecast.html" şi apoi operând în aplicaţia deschisă în browser – am obţinut cam în 3-4 minute (prin 15 operaţii "SWAP") următoarea variantă de plasare corectă a lecţiilor cuplate:
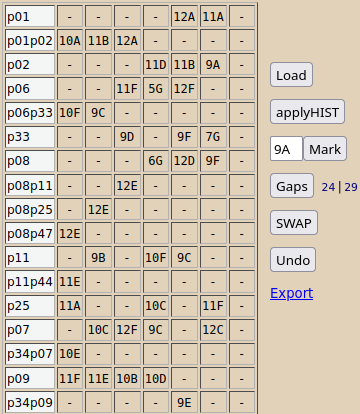
Prin link-ul "Export" am salvat orarul astfel modificat, în "orar_Lu_2.csv"
Să observăm că numărul de ferestre s-a mărit la 29; dar de fapt, acest număr nu mai este cel corect: de exemplu, p01 are o fereastră „ascunsă”, dat fiind că face primele 3 ore împreună cu p02 (orele puse profesorului fictiv "p01p02") şi apoi trebuie să stea o oră, pentru a ajunge la orele proprii (a 5-a la 12A şi a 6-a la 11A); iar lui p11 i s-a socotit o fereastră (având "- 9B - 10F 9C"), dar de fapt este o fereastră aparentă, fiindcă în ora a 3-a intră împreună cu p08 la clasa 12E.
p34 are chiar 3 ferestre (ascunse): intră ora I-a împreună cu p07 la 10E şi apoi tocmai ora a 5-a, împreună cu p09, la clasa 9E (şi consultând dedesubtul liniilor din imaginea parţială redată mai sus, constatăm că p34 nu are alte ore).
Vom vedea mai jos că numărul (corect) de ferestre (ascunse sau nu) din orarul obţinut mai sus este 37.
Reducerea ferestrelor, ţinând seama şi de cuplaje
Reluăm într-un nou fişier, programul recast.R din [3]; s-ar cuveni o anumită reorganizare a codului respectiv, dar deocamdată doar am mutat unele funcţii în "stmt_utils.R"; păstrăm deocamdată (şi nu le mai redăm aici) funcţiile move_cls(), cover_gaps(), choose_min(), recast() şi search_better().
# vrecast.R reduce numărul de ferestre (reale sau aparente) din orarul zilei source("stmt_utils.R") # get_bin_patt(), cnt_holes(), prnTime() load("messing.RDS") # Lx1, Lx2 (cuplajele din cursul săptămânii) # Preia orarul unei zile; asumăm că orele cuplate nu se suprapun. X <- read_csv("orar_Lu_2.csv", col_types = "cccccccc") prof_day <- unique(X$prof) # profesorii (şi cei fictivi) pe ziua curentă Lx1 <- select_cupl(Lx1, prof_day) Lx2 <- select_cupl(Lx2, prof_day) nx1 <- names(Lx1); nx2 <- names(Lx2) MXT <- as.matrix(X[, 2:ncol(X)]) # matricea orelor row.names(MXT) <- X$prof nHm <- ncol(MXT) # nr. maxim de ore ale unei clase (7)
Am evidenţiat mai sus cazul profesorului p34, care în ziua "Lu" nu are ore proprii, dar este implicat în cuplajele "p34p07" şi "p34p09"; o distanţă mai mare ca 1 între orele alocate acestora înseamnă cel puţin o fereastră (ascunsă), pentru p34.
Următoarea funcţie produce un vector conţinând una după alta, câte o pereche de cuplaje care implică un profesor fără ore proprii în ziua respectivă:
# profesorii fără ore proprii, implicaţi în cel puţin două cuplaje special_cases <- function() { spc <- map_df(nx2, function(cup) { cpl <- split_cuplu(cup) pr <- setdiff(cpl, nx1) if(length(pr) == 1) return( data.frame(prof = pr, cup = cup) ) }) onc <- spc[duplicated(spc$prof), ]$prof sort(spc[spc$prof %in% onc, ]$cup) } p_sp <- special_cases() # [1] "p34p07" "p34p09"
Următoarele funcţii determină numărul de ferestre (incluzând acum şi pe cele ascunse) dintr-o matrice orară (precum cea iniţială, MXT), pe baza vectorului de şabloane binare asociat acelei matrici prin get_bin_patt():
cnt_all_gaps <- function(vsb) { # vectorul şabloanelor orare holes_cupl <- function() { ng <- 0 for(p in nx1) { B <- vsb[p] for(pr in Lx1[[p]]) B <- bitwOr(B, vsb[pr]) ng <- ng + cnt_holes(B) } # adaugă eventual, diverse cazuri particulare: if(length(p_sp) >= 2) { for(i in seq(1, length(p_sp), by=2)) ng <- ng + cnt_holes(bitwOr(vsb[p_sp[i]], vsb[p_sp[i+1]])) } ng } sum(unlist(lapply(vsb, cnt_holes))) + holes_cupl() } # numărul ferestrelor din orar, ţinând cont şi de cuplaje count_gaps <- function(morr) morr %>% get_bin_patt(.) %>% cnt_all_gaps(.)
Următoarea funcţie analizează şabloanele orare ale profesorilor fictivi (constituite până la momentul curent), pentru a vedea dacă nu cumva există lecţii cuplate care s-ar suprapune (având câte un bit '1' într-o aceeaşi poziţie din şabloanele binare respective):
# verifică suprapunerea lecţiilor profesorilor cuplaţi vrf_over <- function(morr) { bith <- get_bin_patt(morr) for(prf in nx2) { B <- 0L for(pc in Lx2[[prf]]) B <- bitwOr(B, bith[pc]) if(bitwAnd(bith[prf], B) > 0) return(FALSE) } TRUE # lecţiile cuplate de profesorii fictivi NU se suprapun }
În final, invocând ca şi în [3] search_better(Niter=3000), obţinem în câteva minute, un orar cu 7 sau cu 6 ferestre – de exemplu:
[1] 37 (numărul iniţial de ferestre) 1 2 3 4 5 6 7 1 2 3 4 5 6 7 p01 - - - 12A 11A - - p19 - - 9D 12C 12E 10D - p01p02 12A 11B 10A - - - - p20 12F 11A 10F 8G - - - p02 - - - 11D 9A 11B - p21 10A 10D 7G 12E - - - p06 - - - 5G 12F 11F - p22 - - 12B 9B 12D 10B - p06p33 - 10F 9C - - - - p23 - - 11F 9F 12C 11A - p33 - - - 9D 7G 9F - p24 - 9A - 7G 6G 12B - p08 - - - 12D 9F 6G - p26 11F 12F - - 11E 9D - p08p11 - 12E - - - - - p27 9E 12D 11D 10E - - - p08p25 - - 12E - - - - p28 10E 11C 11B - - - - p08p47 12E - - - - - - p29 12B 9D 12C - - - - p11 - - - 10F 9B 9C - p30 11C 12B 12A - - - - p11p44 11E - - - - - - p31 10D 9B 11C - - - - p25 - - - 11A 11F 10C - p32 7G 10B 9A - - - - p07 - 12C 12F 9C 10C - - p35 10F 10C 11A - - - - p34p07 - - - - - 10E - p36 - - - 9A 12A 10A - p09 10B 11F 11E 10D - - - p37 9F 9C - - - - - p34p09 - - - - 9E - - p38 10C 9E - - - - - p03 9C 11E 9B 9E 10E 10F - p39 9D 10E 9E - - - - p04 - 12A 10E 12F 11D 5G - p40 11A 7G - - - - - p05 11B 8G 10C - 10B 9A - p42 12C 6G - - - - - p10 9B 11D 9F 11E 9C - - p45 5G 9F - 6G 10F - - p12 - - - 11B 10D 12F 10A p46 - - - - 5G 8G 10E p13 - - - 10A 11B 9E 8G p49 12D - - - - - - p14 9A 10A 8G 11F - - - p50 6G - - - - - - p15 - - 12D 10B 10A 12E - p56 8G 5G 6G - - - - p16 - - 10D 10C 12B 9B - p58 11D - - - - - - p17 - - 5G 12B 11C 12A - p61 - - - - 8G - - p18 - - 10B 11C 9D 12C - p62 - - - - - 7G - [1] 6 (numărul final de ferestre)
Cele 37 de ferestre din orarul iniţial au fost reduse la 6: una ascunsă, la p11 (intră la prima oră împreună cu p44 la clasa 11E, a doua oră cu p08 la 12E şi de la a 4-a oră îşi face orele proprii), trei ferestre de câte o oră (la p05, p24 şi p45) şi o fereastră de două ore consecutive (la p26). Exceptând p11, profesorii care intră în cuplaje nu au ferestre; de exemplu, p06 şi p33 fac împreună ora a 2-a şi a 3-a (la 10F şi 9C), apoi continuă fiecare cu cele câte trei ore proprii; să mai observăm că p34 (care nu are ore proprii, dar intră în două cuplaje) nu are fereastră.
Repetând search_better(), obţinem orare cu alte repartizări a celor 6 ferestre, în timpi care oscilează între câteva minute şi circa 30 de minute (în funcţie şi de valoarea aleasă pentru Niter); ar fi de văzut dacă extinzând cumva gama de „reparaţii” constituită de cover_gaps() (vizând explicit şi ferestrele „ascunse”), am obţine şi orare cu mai puţin de 6 ferestre…
vezi Cărţile mele (de programare)