În [2] am evidenţiat (indirect) că focarele unei elipse care este tangentă în origine axei $\mathsf{O}x$ sunt situate pe o anumită cardioidă, simetric faţă de o dreaptă care trece prin vârful unei anumite parabole; cum am găsi totuşi - fixând lungimea semiaxei mari - ecuaţiile acestor elipse?

De regulă, "ecuaţia generală" a elipsei angajează ca parametru unghiul cu $\mathsf{O}x$ al axei mari (v. Ellipse); dar în cazul nostru putem profita de proprietatea evidenţiată mai sus, folosind parametrizarea din [1] a cardioidei: având (după [1] şi [2]) focarele $\mathsf{P}_t$ şi $\mathsf{Q}_{1-t}$ cu $t\in[0,\frac{1}{2}]$, ecuaţiile elipselor rezultă plecând de la exprimarea lungimii fixate a axei mari ca suma distanţelor la focare ale punctului generic $(x,y)$: $$\sqrt{(x-x_p)^2+(y-y_p)^2}=2a-\sqrt{(x-x_q)^2+(y-y_q)^2}$$ unde $\mathsf{P}_t\left(x_p=2at(2t-1), y_p=4at\sqrt{t(1-t)}\right)$; schimbând $t\rightarrow 1-t$ avem şi coordonatele lui $\mathsf{Q}_{1-t}(x_q, y_q)$. Ridicăm la pătrat, separăm radicalul, apoi ridicăm iarăşi la pătrat şi ţinem seama de aceste exprimări intermediare: $$\begin{array}{@{}cll} x_p-x_q &=& 2a(2t-1) \\ y_p-y_q &=& 4a(2t-1)\sqrt{t(1-t)} \\ x_q^2-x_p^2 &=& 4a^2(2t-1)^2(1-2t) \\ y_q^2-y_p^2 &=& 16a^2t(1-t)(1-2t) \\ \end{array}$$

Rezultă un polinom de gradul doi în $x$ şi $y$; desigur că a fost ceva de muncă, dar măcar am putut evita calculul termenului liber şi coeficientului lui $x$ (ambii zero, fiindcă elipsa este tangentă în $\mathsf{O}$ axei $y=0$).
În final avem această teoremă (care sintetizează [1] şi [2]):

Ecuaţiile elipselor din semiplanul superior, centrate la dreapta axei $\mathsf{O}y$, cu aceeaşi lungime a semiaxei mari şi tangente în $\mathsf{O}$ axei $\mathsf{O}x$ sunt $Ax^2+Bxy+Cy^2+Ey=0$, unde pentru $t\in[0,\frac{1}{2}]$: $$\begin{array}{@{}cll} A &=& 4t(1-t) \\ B &=& -4(2t-1)^2\sqrt{t(1-t)} \\ C &=& 16t^2(1-t)^2+(2t-1)^2 \\ E &=& -16at(1-t)\sqrt{t(1-t)} \\ \end{array}$$ şi unde $2a$ (care apare numai la $E\,$) este lungimea comună (fixată) a axelor mari.
Centrele acestor elipse sunt situate pe arcul de parabolă $y=\sqrt{a(a-x)},\,x\in[0,a]$ iar axele mici trec toate prin vârful acestei parabole; focarele acestor elipse sunt situate pe cardioida de ecuaţie $(x^2-ax+y^2)^2-a^2(x^2+y^2)=0$ (descriind semi-cardioida superioară).

Pentru o reprezentare grafică, avem mai jos programul R corespunzător acestor elipse:

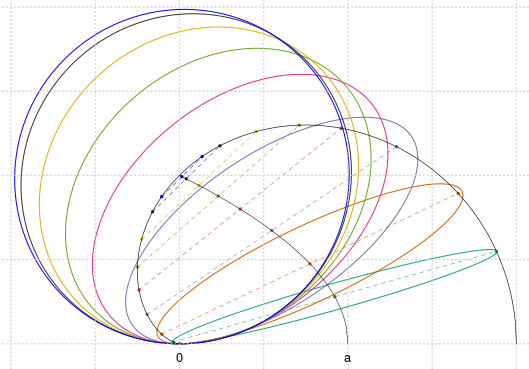
require(RColorBrewer)
kol <- c(brewer.pal(6, "Dark2"), "gray20", "blue")

a <- 1  # semiaxa mare a elipselor
plot(0, type="n", asp=1, xaxt="n", yaxt="n", bty="n", xlab="", ylab="", 
     xlim=c(-a, 2*a), ylim=c(0, 2*a)); grid()  # setează fereastra grafică

plot_path <- function(func2, ...) {  # plotează funcţii implicite
    u <- seq(-a, 2*a, by=0.01)
    v <- seq(0, 2*a, by=0.01)
    Z <- outer(u, v, func2)  # valorile f(x,y), indexate după x şi y
    contour(u, v, Z, levels = c(0), drawlabels=FALSE, add=TRUE, ...)  # f(x,y) = 0
}
elli <- function(x, y) {  # ecuaţia elipsei, cu 'l' fixat dinafară
    A <- 4*l*(1-l)
    B <- -4*(2*l-1)^2*sqrt(l*(1-l))
    C <- 16*l^2*(1-l)^2 + (2*l-1)^2
    E <- -16*a*l*(1-l)*sqrt(l*(1-l))  # print(c(A, B, C, E))
    A*x^2 + B*x*y + C*y^2 + E*y
}
k <- 1  # index în paleta de culori
for(l in c(0.02, 0.06, 0.13, 0.2, 0.26, 0.33, 0.4, 0.44)) {
    plot_path(elli, col=kol[k])  # plotează elipsa, pentru 'l' curent
    centru <- a*(2*l-1)^2 + 1i*2*a*sqrt(l*(1-l))
    focare <- c(2*a*l*(2*l-1)+1i*4*a*l*sqrt(l*(1-l)), 
                2*a*(1-l)*(1-2*l)+1i*4*a*(1-l)*sqrt(l*(1-l)))
    points(c(centru, focare), col=kol[k], pch=20, cex=0.5)
    segments(Re(focare[1]), Im(focare[1]), 
             Re(focare[2]), Im(focare[2]), lwd=0.5, lty="dashed", col=kol[k])
    k <- k+1
}
x <- seq(0, a, by=0.01)
y <- sqrt(a*(a-x))
points(x, y, type="l", lwd=0.5)  # plotează arcul de parabolă

l <- seq(0, 1, by=0.001)
x <- 2*a*l*(2*l-1)
y <- 4*a*l*sqrt(l*(1-l))
points(x, y, type="l", lwd=0.6)  # plotează semi-cardioida (v. [1])
text(c(a+0i, 0i), labels=c("a", "0"), pos=1, cex=0.8)

Simetrizând faţă de axe, putem formula mai general teorema de mai sus: elipsele cu axa mare de o aceeaşi lungime şi care sunt tangente într-un acelaşi punct $\mathsf{O}$ unei aceleiaşi drepte $d$, au centrele pe două arce de parabolă simetrice faţă de perpendiculara în $\mathsf{O}$ pe $d$ şi au focarele pe două cardioide care au nodul în $\mathsf{O}$, au axa pe $d$ şi sunt simetrice faţă de perpendiculara în $\mathsf{O}$ pe $d$.