Se împlinesc 60 de ani, de când Stanisław Ulam a experimentat (în 1963) această idee: așezăm într-o matrice n×n numere naturale consecutive, spiralând în jurul centrului ei; este de observat cum apar numerele prime – apar „la întâmplare”, sau cumva, respectă (într-o anumită măsură) vreun anumit șablon (sau poate, anumite orientări)?

Dacă privim urmele lăsate de minge pe terenul de tenis, după trei ore de joc – suntem îndreptățiți să apreciem că urmele sau punctele respective sunt distribuite nealeatoriu, pe teren; comparând densitatea punctelor pe anumite zone (în corelație cu fiecare jucător), specialiștii pot deduce preferințele, abilitățile și planurile de joc ale celor doi parteneri.
Cam la fel ar sta lucrurile în cazul distribuției numerelor prime pe o spirală a numerelor… doar că în acest caz, aspectul nealeatoriu are cauze greu de deslușit.

Demult avem, un fișier-text cu numerele prime de sub 10⁷ (comprimat, are cam 1.7Mb); l-am citit într-o sesiune de lucru cu R și l-am salvat în formatul specific, în fișierul "Primes.RDS", încât acum putem miza direct măcar pe lista numerelor prime până la 9 999 991.

Prima abordare

Alegem să montăm o variantă „economică” de spirală Ulam, în care ignorăm numerele pare; deocamdată constituim o matrice nu prea mare, încât să putem și vizualiza cifrele.
Ne bazăm pe funcția sp_walk() din [1], care furnizează corespondența dintre rangurile de linie și coloană pe de o parte și indecșii nodurilor spiralei din centrul matricei:

Primes <- readRDS("Primes.RDS")
n <- 25
N <- n*n
sqi <- seq(1, by = 2, length = N)  # primele N numere impare
prm <- Primes[Primes <= sqi[length(sqi)]]  # numerele prime, între cele N
rcv <- sp_walk(n)  # rang linie, coloană și index asociat pe spirală
M <- matrix(0L, nrow = n, ncol = n, byrow=TRUE)
for(k in 1:N)
    M[rcv$R[k], rcv$C[k]] <- sqi[k]

Am constituit matricea spiralată M, conținând primele 25×25 numere impare; afișăm partea centrală, evidențiind prima buclă a spiralei (încheiată la numărul 13; v. [1]):

> q <- n%/%2 + 1; sq <- (q-2):(q+2); print(M[sq, sq])
             [,1] [,2] [,3] [,4] [,5]
        [1,]   33   31   29   27   25
        [2,]   35    9    7    5   23
        [3,]   37   11    1    3   21
        [4,]   39   13   15   17   19
        [5,]   41   43   45   47   49

Probabil că o putem afișa în întregime și în „modul text”, dar anticipând și matrici mai mari – preferăm să plotăm în fereastra grafică, printr-o secvență pe care am mai folosit-o anterior; plecăm de la un set de abscise echidistante Xi și prin expand.grid() constituim o grilă (colorată ca tabla de șah, prin rect()) și înscriem numerele din matrice prin text() – evidențiind prin culoare (blue) pe cele care sunt prime (subliniem că în text() și points() trebuie să angajăm transpusa matricei, pentru a respecta și grafic, formatul inițial al acesteia):

opar = par(mar = c(0, 0, 0, 0), lwd = 0.01, cex = 0.58)
plot(c(0, 12*n), c(0, 12*n), asp = 1, type = "n",  # setează fereastra grafică
     bty = "n", xaxt = "n", yaxt = "n", xlab = "", ylab = "")
Xi <- 12 * (0:(n-1))
fields <- expand.grid(Xi, Xi)  # coordonatele colţurilor (i, j), i,j ∈ Xi
f1 <- fields[, 1]  # abscisele colţurilor
f2 <- fields[, 2]  # ordonatele acestora
rect(f1, f2, f1 + 11, f2 + 11,  # colorează alternativ câmpurile grilei
     col = ifelse((f1 %/% 12 + f2 %/% 12) %% 2, "white", "gray95"))
text(f1+5, f2+5, t(M[n:1, ]), font=2, family="mono",  # înscrie numerele
     col = ifelse(t(M[n:1, ]) %in% prm, "blue", "gray30"))
par(opar)

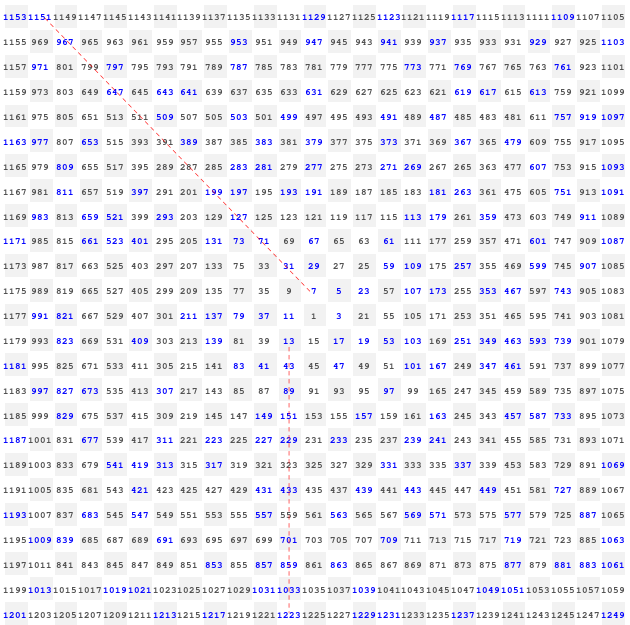
S. Ulam a observat și apoi a întărit experimental pe matrici cât de mari se putea atunci, că dispunerea numerelor prime are un aspect nealeatoriu (… deschizând o „cutia Pandorei”).

Pe matrici mici, cum avem mai sus, putem verifica direct unele fapte (v. oeis.org/wiki); de exemplu, diagonala care pleacă din 7 spre stânga-sus (trasată cu roșu) conține numerele prime 7, 31, 71, 127, 199, 647, 967, 1151 (și continuă dincolo de margini cu 1567, etc.) – toate, de forma $8n^2-1$ (de exemplu, 199=200-1=8×5²-1).
Pentru alt exemplu, verticala din 13 în jos (trasată și ea cu roșu) conține numere prime de forma $8n^2+6n-1$, dintre care primele 10 (pentru $n=1..10$) se văd pe imaginea redată mai sus.

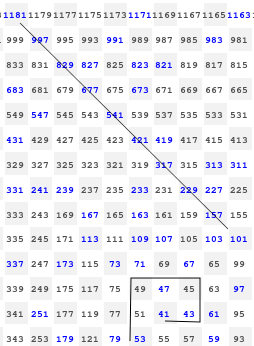
Desigur, putem face încă fel de fel de experimente; de exemplu, în loc să începem de la 1, să plecăm de la un alt număr impar – fie 41 (care este și prim):

sqi <- seq(41, by = 2, length = N)
prm <- Primes[Primes >= sqi[1] & 
              Primes <= sqi[length(sqi)]]

Cu această singură modificare, programul redat mai sus produce o matrice 25×25 în care numerele (impare, toate) spiralează în jurul lui 41; redăm alăturat un extras, pe care observăm o diagonală pe care toate numerele redate sunt prime.

Ne putem pune această problemă (a câta…; v. [1]):
să găsim forma numerelor respective.

Deci căutăm $f(n)=an^2+bn+c$ încât să avem $f(1)=\mathbf{101}, f(2)=\mathbf{157}, f(3)=\mathbf{229}$. Rezolvând sistemul de ecuații respectiv, găsim $f(n)=8n^2+32n+61$; putem verifica ușor că acest polinom generează cele 10 numere prime care apar consecutiv pe diagonala arătată:

> sapply(1:10, function(n) 8*n^2 + 32*n + 61)
# [1]  101  157  229  317  421  541  677  829  997 1181

Pentru $n=11$ și $n=12$ încă obținem numere prime, dar $f(13)=1829$ nu mai este un număr prim (=59×31), nici $f(14)$ (dar $f(15)=2341$ este prim și apare undeva, pe acea diagonală).

Precizăm că am ales 41 drept centru al spiralei, amintindu-ne de polinomul introdus de Euler $n^2+n-41$, care generează numere prime pentru $n=1..40$; aceste 40 de numere prime sunt situate – chiar consecutiv – pe o aceeași diagonală a spiralei Ulam centrate în 41, dacă aceasta conține toate numerele ≥41 (nu numai pe cele impare, ca în varianta de mai sus).

Un mic experiment de simplificare

Mai sus, pentru dimensiune mică de matrice, am putut afișa numerele ca atare (în baza 10) – dar se cuvine să renunțăm la aceasta, pentru matrici mai mari: în fond ceea ce ne interesează este calitatea de număr prim, nu cifrele.

În secvența de plotare de mai sus, micșorăm abscisele Xi și eliminăm liniile rect() și text() – adăugând în schimb (pentru a plota puncte, în loc de a afișa numere):

points(f1+2, f2+2, pch='*',
       col = ifelse(t(M[n:1, ]) %in% prm, "blue", "gray85"))

Acum – repetând execuția programului, astfel modificat – numerele sunt redate printr-un caracter cu o culoare sau alta, după caz (prim, sau compus), ceea ce și ușurează, perceperea vizuală a unor șabloane sau formațiuni:

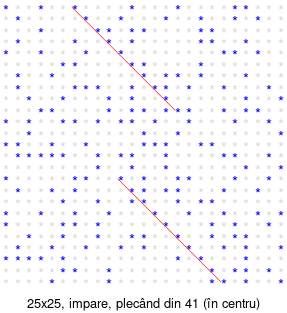
Figura obținută corespunde spiralei din 41 (centrul matricei 25×25, formată numai din numerele impare ≥41); am marcat cu roșu două diagonale, pe care se află consecutiv câte 10 numere prime – dintre care cea care pleacă de la prima linie corespunde numerelor extrase mai sus (101, 157, 229, etc. – pentru care găsisem polinomul $f(n)=8n^2+32n+61$).
Ca să găsim numerele de pe a doua diagonală, ținem cont că ea pleacă (socotind pe imagine) din coloana 20 a ultimei linii și se încheie în linia 16, coloana 11:

> diag(M[25:16, 20:11])  # furnizează elementele diagonalei submatricei
# [1] 1279 1087  911  751  607  479  367  271  191  127

Procedând ca și în cazul anterior, găsim că polinomul care generează aceste numere este $f(n)=8n^2 + 40n + 79$ (pentru $n=1..10$; de exemplu $f(5)=8*25+40*5+79=479$).

Desigur, deducerea polinomului $f(n)$ este lesne de făcut, dacă păstrăm numerele în matricea M și dacă putem deduce de pe figura plotată pe ce linie și coloană se află punctul…

Dar dacă în loc de numere, afișăm "1" sau "0" după cum numărul este prim sau nu – de ce să mai păstrăm numerele, în matricea M? Putem înscrie direct valori logice TRUE și FALSE, care în principiu, se pot reprezenta pe câte un singur bit – încât M ar ocupa cea mai mică posibil, zonă de memorie (și astfel, M poate fi și foarte mare)… De fapt însă, lucrurile nu stau așa:

> object.size(1:100)  # 448 bytes (întregi "scurți")
> object.size(sample(rep(c(TRUE,FALSE), 50)))  # 448 bytes ("valori logice")

Deducem că valorile logice sunt reprezentate la fel ca și numerele întregi, pe câte 4 octeți (32 de biți) de memorie (și nicidecum, pe câte un bit); explicația ar ține tot de principii: R fiind destinat analizei statistice a seturilor de date, a trebuit să se aibă în vedere situația foarte obișnuită, când o variabilă logică are în setul respectiv și date „lipsă”, nu numai cu valori TRUE/FALSE (în plus, trebuie să se țină seama și de faptul că memoria se accesează pe octeți sau pe multipli de octet, nu pe biți individuali).
Obs. Constantele întregi sufixate cu 'L' (ca "0L") și întregii din secvențele generate prin operatorul ":" (ca mai sus, 1:100) ocupă în memorie câte 32 de biți; altfel (depinzând și de sistemul subiacent), întregii sunt memorați ca și „numerele reale”, pe câte 64 de biți.

A doua abordare

Să parametrizăm obținerea matricei-spirale M: putem plasa în centru un număr natural oarecare (desigur, în limitele admise de tipul integer); numerele din matrice sunt cele dintr-o progresie aritmetică oarecare, începând de la valoarea indicată în centru; matricea are o lățime (număr de coloane) oarecare, eventual cât de mare se poate; în plus, matricea poate conține fie chiar numerele respective, spiralate în jurul centrului, fie doar valori 1 și 0, indicând ce fel de număr (prim sau nu) s-ar afla în fiecare linie și coloană:

sq_spiral <- function(Orig, Pas, Width, logi=TRUE) {
    N <- Width * Width
    sqi <- seq(Orig, by = Pas, length = N)
    prm <- Primes[between(Primes, sqi[1], sqi[length(sqi)])]
    rcv <- sp_walk(Width)  # v. [1]
    M <- matrix(0L, nrow = Width, ncol = Width, byrow=TRUE)
    if(logi) {
        for(k in 1:N) 
            if(sqi[k] %in% prm)
                M[rcv$R[k], rcv$C[k]] <- 1L
    } else {
        for(k in 1:N)
            M[rcv$R[k], rcv$C[k]] <- sqi[k]    
    }
    M
}

Reluăm – cu adaptările cuvenite – secvența de plotare de mai sus, pentru matricea binară 100×100 care caracterizează numerele prime dintre numerele impare ≥59, spiralate în jurul centrului (care corespunde numărului prim 59):

M <- sq_spiral(59, 2, 100)  # cu valori 1 (număr prim) și 0
n <- nrow(M)
opar = par(mar = c(2, 2, 2, 2), lwd = 0.01, cex = 0.6)
plot(c(0, 2*n), c(0, 2*n), asp = 1, type = "n",
     bty = "n", xaxt = "n", yaxt = "n", xlab = "", ylab = "")
Xi <- 2 * (0:(n-1))  # abscisele de reprezentare a valorilor din M
fields <- expand.grid(Xi, Xi)  # toate perechile (i, j), i,j ∈ Xi
f1 <- fields[, 1]  # abscisele "colţurilor"
f2 <- fields[, 2]  # ordonatele acestora
points(f1, f2, pch="*", col = ifelse(t(M[n:1, ]), "blue", "gray95"))
mtext("100^2 impare, spiralând antiorar din centrul 59", cex=0.8, side=1)
par(opar)
mij <- n %/% 2 + 1  # marchează centrul matricei
points(Xi[mij]-2, Xi[mij]-2, col="red", cex=0.4)

Pe imaginea produsă putem distinge mai multe linii (diagonale, orizontale, sau verticale) care conțin fiecare, multe puncte (numere prime).

O mică investigație

Să depistăm numerele prime – și apoi, să aflăm forma acestora – corespunzătoare punctelor dispuse orizontal și respectiv vertical (în grupuri relativ compacte, cum vedem pe figură), plecând fie chiar din centrul imaginii (spre dreapta), fie dintr-un punct vecin acestuia:

> M <- sq_spiral(59, 2, 100, FALSE)  # M conține acum numerele impare 59..20057
> lmj <- M[mij, mij:100]  # pe linia centrală, spre dreapta
> lmj <- lmj[lmj %in% Primes]  # numere prime, de la centru spre dreapta
# [1]    61    79   113   163   229   311   409   523   653  1543  2011  2269
#[13]  2543  2833  3461  4153  4523  4909  6163  7079  7561  8059  8573  9103
#[25]  9649 10211 10789 11383 12619 14593 17449 18973 19759

Acestor numere prime le corespund cele 33 de puncte din imaginea de mai sus, de la dreapta punctului marcat cu roșu (centrul 59), aflate pe aceeași orizontală cu acesta.
Un polinom care generează toate aceste numere (de fapt, toate numerele, inclusiv pe cele neprime, aflate la dreapta lui 59) este $f(n)=8n^2-6n+59$:

> fn <- sapply(1:50, function(n) 8*n^2 - 6*n + 59)
> fn[fn %in% Primes]  # rezultă cele 33 de numere prime din lmj (redate mai sus)

lmj <- M[mij+1, (mij-1):1]
# [1]    73    71    97   139   197   271   361   467   589   727   881  1051
#[13]  1237  1439  1657  1891  2141  2407  2689  2987  3301  3631  3977  4339
#[25]  4717  5111  5521  5947  6389  6847  7321  7811  8317  8839  9377  9931
#[37] 10501 11087 11689 12307 12941 13591 14257 14939 15637 16351 17081 17827 18589 19367

Am redat toate cele 50 de numere, fiindcă întâi am procedat ca și în cazul precedent: am pus (mecanic) condițiile $f(1)=73$, $f(2)=71$ și $f(3)=97$ – constatând însă că polinomul $f(n)$ determinat astfel nu generează și celelalte numere ($f(4)\ne 139$, de exemplu)…
Ne-am amintit în sfârșit, de polinomul de interpolare al lui Netwon; în particular, niște valori date rezultă dintr-un același polinom de gradul doi $f(n)$ când $n$ ia valori consecutive, dacă și numai dacă diferențele de ordinul doi ale valorilor respective sunt egale – ceea ce este foarte ușor să verificăm, în cazul nostru:

> diff(diff(lmj))
# [1] 28 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16
#[26] 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16

Se vede că toate diferențele dintre fiecare număr din lmj și precedentul acestuia devin egale dacă repetăm diferențierea de două ori și dacă omitem primul număr, 73; prin urmare, cele 49 de numere din lmj[-1] pot fi generate printr-un același polinom de gradul doi (și nu va mai fi necesar, ca în cazul precedent, să și verificăm prin sapply, că obținem toate numerele respective).
Pentru primele 3 numere avem acest tabel de diferențe:

        n  f(n)  Δ1  Δ2
        1   71
        2   97   26
        3  139   42  16

Deci polinomul de interpolare căutat este $f(n)=71+26(n-1)+\frac{16}{2!}(n-1)(n-2)$; rezultă că numerele aflate pe orizontală în stânga lui 73 sunt generate de $f(n)=8n^2+2n+61$; dintre aceste 49 de numere, 31 se găsesc în Primes.
Fiindcă $f(1)=71$, toate numerele $f(1+71k),\,k\ge 1$ sunt multipli de 71 (primul fiind $f(72)=71*587=41677$) – sunt aceștia situați și ei, undeva mai departe, pe diagonala formată de cele 49 de numere evidențiate mai sus?

Putem investiga la fel și alte linii; se constată că există mai multe linii (mai ales, diagonale) pe care proporția numerelor prime este în jur de 60%.

Cea mai simplă abordare

Folosind funcția image(), putem avea imediat, imaginea grafică a matricei M (cu elemente 1 și 0), chiar pentru dimensiuni relativ mari:

M <- sq_spiral(41, 1, 250)  # 41..62540  (cu 6267 numere prime)
image(t(M), xaxt = "n", yaxt = "n")

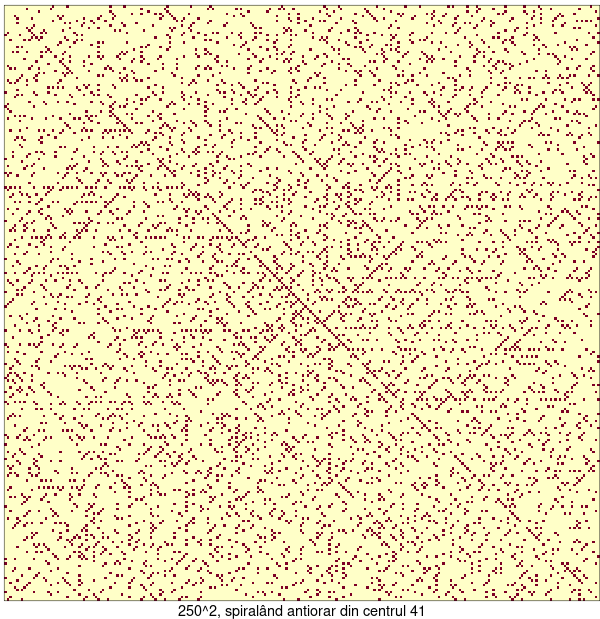
Am redat o matrice nu tocmai mare – are abia 6267 puncte (reprezentând numere prime), însă acestea sunt încă suficient de lizibile pentru a permite (…dacă n-avem altceva de făcut) investigații precum cele întreprinse pe linii, mai sus; pentru o matrice 500×500 (încă mică – are abia 22037 de numere prime), punctele nu mai pot fi identificate după linii și coloane.

Putem verifica ușor că dacă am dispune aleatoriu elementele matricei M (folosind sample() și apoi, transformând vectorul rezultat în matrice), atunci pe imaginea rezultată nu mai apar diagonale de numere prime (cum distingem pe imaginea de mai sus):

> S <- sample(M)  # int [1:62500] 0 0 0 1 0 0 0 0 0 0 ...
> dim(S) <- c(n, n)
> image(S, xaxt = "n", yaxt = "n")

Se pot observa multe aspecte ale distribuției numerelor prime pe o spirală Ulam… dispunerea pe o diagonală a unor numere prime depinde sau nu, de centrul ales pentru spirala respectivă? (dacă schimbăm centrul, numerele prime respective rămân situate pe o diagonală?); etc. Dar justificarea acestor aspecte (și chiar necesitatea justificării) rămâne (și după 60 de ani de când au început să apară) o problemă neînțeleasă.