Înapoi, de la orar (PDF) la matricea de încadrare
[1] De capul meu prin problema orarului şcolar (pe Google Play)
Ceea ce ne trebuie ca să construim un orar este matricea de încadrare, care sintetizează legăturile dintre profesori şi clase; pe baza acesteia constituim setul tuturor lecţiilor prof | cls şi pentru a asocia încadrării date, un orar sau altul – montăm o coloană pentru alocarea după anumite principii, a zilelor şi una pentru alocarea pe orele zilei a lecţiilor.
Pentru a experimenta această idee şi a pune la punct programele de alocare necesare (v. [1]), am folosit orare existente (într-o formă finală) pe site-urile unor licee – trebuind deci să deducem din orarul prezentat, matricea de încadrare.
Cea mai bună prezentare de orar pe care am găsit-o este aceasta:
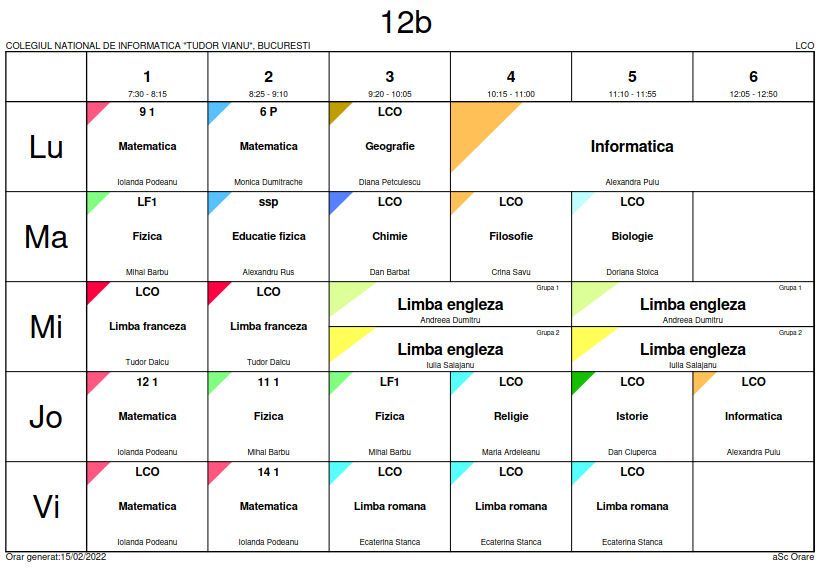
Fişierul PDF respectiv prezintă consistent şi (aparent) unitar, orarul câte unei clase (mai sus am redat pagina clasei "12b") – consemnând: numele complet (şi corect: nu cu majuscule) al disciplinei şcolare de care aparţine fiecare lecţie (lipsesc doar diacriticele); numele profesorului care face acea lecţie (fără prefixul vax "Prof."); intervalul de timp (ziua şi ora) în care se desfăşoară lecţia; şi o indicaţie (cam de prisos, repetându-se frecvent la o aceeaşi clasă) asupra locului sau sălii de clasă în care va decurge lecţia.
Icon-urile triunghiulare adăugate pe celule în colţurile stânga-sus sunt inspirate: asigură o mai bună separare vizuală pe linii (şi coloane), iar prin mărime evidenţiază întinderea lecţiilor (fie ca de obicei, pe o singură oră – fie pe două sau trei ore consecutive, cu întreaga clasă, sau cu câte o grupă).
Dar pe noi nu ne interesează să consultăm orarul vreunei clase – scopul asumat prin formatul PDF/Excel/HTML – şi nici numele profesorilor (altfel… observam lipsa diacriticelor şi forma elegantă dar nestandard, "Prenume Nume"); ne interesează „matricea de încadrare” şi eventual, principiile (sau interesele) pe baza cărora s-a generat (prin ascTimeTables) orarul respectiv.
Iar ceea ce (pe lângă eleganţa şi corectitudinea prezentării) ne-a atras atenţia, ţine tocmai de „principii” (v. [2]): lecţiile sunt repartizate cât se poate de neuniform.
La fiecare clasă, lecţiile unui aceluiaşi obiect sunt grupate în câte o aceeaşi zi (sau în două-trei zile); de exemplu, la clasa "12b" redată mai sus, cele 3 ore de "Limba romana" se fac toate, în ziua "Vi" (şi nu câte una pe zi).
Dar – fiind vorba de un liceu dintre cele mai bune – probabil că elevii nu au de suferit din cauza acestei inversări a „dogmei” repartizării echilibrate a orelor. Dacă vrem vom putea totuşi deduce, dacă este vorba de „principii”, sau de interese (asigurarea unui program de lucru confortabil profesorilor – fără ferestre, cu zile sau jumătăţi de zi libere).
Extragerea directă, din fişierul PDF
Anterior (v. [3], de exemplu), pentru a extrage datele din fişierul PDF care prezenta orarul şcolii, transformam din PDF în Excel, printr-un serviciu extern (oferit de Adobe sau de iLovePDF.com) şi angajam apoi un pachet R pentru a citi foile Excel respective.
De fapt, putem citi direct din fişierul PDF – folosind programul utilitar pdftotext (din pachetul poppler-utils, inclus în Ubuntu-Linux), sau prin pachetul echivalent R pdftools, sau (cel mai direct) folosind interpretorul Ghostscript.
Consultând pur şi simplu, fişierul rezultat – descoperim uşor defectele ascunse în prezentarea PDF de la care am plecat; iar cea mai simplă cale pentru corectarea acestor „defecte” constă în editarea directă a fişierului-text obţinut, înainte de a începe să ne ocupăm de structurarea ca „set de date”, a datelor respective.
Creem un subdirector în care copiem în TV.pdf, orarul descărcat în prealabil de pe site-ul liceului respectiv; apoi, folosind Ghostscript, extragem textul conţinut în fişierul TV.pdf – obţinând câte un fişier-text pentru fiecare pagină (clasă):
vb@Home:~/22iun$ mkdir TVtxt; cd TVtxt vb@Home:~/22iun/TVtxt$ cp ../2022_02_15_orar-clase.pdf TV.pdf vb@Home:~/22iun/TVtxt$ gs -q -dBATCH -dNOPAUSE \ -sDEVICE=txtwrite \ -sOutputFile='cls-%i.txt' TV.pdf
Pentru a evidenţia despre ce „defecte” ascunse vorbeam mai sus, redăm fişierul cls-1.txt, care corespunde primeia dintre clase:
5
COLEGIUL NATIONAL DE INFORMATICA "TUDOR VIANU", BUCURESTI 6 P
7 8 9 10 11 12
13:20 - 14:05 14:15 - 15:00 15:10 - 15:55 16:05 - 16:50 17:00 - 17:45 17:55 - 18:40
ssp 6 P 6 P 6 P 7 P
Lu Educatie fizica Educatie muzicala Limba engleza Matematica Istorie
Ionela Stan-Cristache Alina Teac Iulia Salajanu Raluca Mangra Veta Grecu
6 P 6 P 6 P 6 P 6 P 6 P
Ma Dirigentie Limba franceza Limba franceza Matematica Educatie vizuala Istorie
Iulia Salajanu Eliza Manz Eliza Manz Raluca Mangra Gratiela Stoian Veta Grecu
S 6 P 6 P 6 P 6 P ssp
Limba engleza Limba engleza Educatie Matematica Limba romana Educatie fizica
Mi tehnologica
Iulia Salajanu Iulia Salajanu Simona Berbec-Rusu Raluca Mangra Ramona Nedea Ionela Stan-Cristache
LF1 6 P 6 P 6 P 6 P 6 P
Jo Religie Geografie Matematica Limba romana Limba romana Limba romana
Maria Ardeleanu Diana Petculescu Raluca Mangra Ramona Nedea Ramona Nedea Ramona Nedea
6 P 6 P 6 P
Vi Informatica Matematica Biologie Educatie sociala
Alina Boca Raluca Mangra Simona Vasilescu Manuela Constantin
Orar generat:15/02/2022 aSc Orare
Pe primul rând avem la mijloc, numele clasei 5 (cu sala de clasă "6 P", indicată la sfârşitul rândului al doilea şi referită apoi pe majoritatea orelor).
Nu ne interesează antetul iniţial "COLEGIUL ..." şi final "Orar generat: ... aSc Orare", nici linia de intervale orare "13:20 - 14:05 ..."; dacă vrem, aceste linii vor putea fi eliminate imediat din toate fişierele, angajând expresii regulate elementare.
Defectul „ascuns” manifestat aici (şi pe orarele celorlalte clase) constă în faptul că liniile corespunzătoare zilelor nu sunt „la fel” formatate; pentru ziua "Mi" formatarea diferă de cea „standard”.
Pentru toate zilele, exceptând "Mi", linia corespunzătoare înregistrează numele disciplinelor, este precedată de linia care conţine numele sălilor de clasă şi este urmată de linia care înregistrează numele profesorilor; în schimb, linia pentru "Mi" mai conţine un singur cuvânt "tehnologica" şi are deasupra nu linia sălilor de clasă (aflată şi mai deasupra), ci linia disciplinelor (iar "Educatie" de pe această linie se leagă dedesubt, cu "tehnologica", reconstituind disciplina "Educatie tehnologica").
Corectarea ar fi simplă: alipim "tehnologica" de "Educatie", înscriem "Mi" la începutul rândului disciplinelor şi apoi ştergem vechiul rând (cel pe care aveam numai "Mi" şi "tehnologica"); dar trebuie să fie clar că este greu de depistat şi de corectat automat asemenea defecte, în toate fişierele rezultate…
Decât să încercăm să constituim vreun procedeu „automat”, care să fie corect în toate cazurile – am preferat să facem manual (folosind un editor de text), câte una-două sau trei corecturi cam de genul indicat mai sus, pentru fiecare fişier cls-*.txt.
Este drept că uneori şi corectura manuală este dificilă:
6 7 8 9 10 ...
12:05 - 12:50 13:20 - 14:05 14:15 - 15:00 15:10 - 15:55 16:05 - 16:50 ...
7 P Grupa 1 LCH 3 D ...
Limba germana
Istorie Valentina Morman Chimie Fizica ...
Lu Grupa 2
Limba germana
Dan Ciuperca Alexandra Tudor Dan Barbat Florina Stan ...
Grupa 1 3 D ...
Limba germana
Valentina Morman Cultură ...
Ma Grupa 2 germană
Limba germana
Alexandra Tudor Alexandra Tudor ...
3 D 3 D Educatie 3 D ...
muzicala
Mi Matematica Biologie Alina Teac Limba romana ...
Educatie
vizuala
Raluca Mangra Mirela Marinescu Gratiela Stoian Ramona Nedea ...
Aici şi "Educatie vizuala" şi "Educatie muzicala" şi "Cultură germană" (… singurul termen cu diacritice!) sunt despărţite pe câte două rânduri (de operat cum am arătat mai sus pentru "tehnologica"); dar mai mult – avem aici şi cuplaje de profesori, pentru "Limba germana" şi pentru "Educatie muzicala | vizuala" (iar termenii separaţi apar fie pe linia care altfel, conţine numele sălilor de clasă, fie pe o nouă linie).
Iată cum am corectat în acest caz (prin operaţii Copy&Paste), pentru a aduce la forma „standard” – constând din exact trei linii: linia sălilor de clasă (şi nu luăm seama la faptul că avem şi "Grupa 1" sau "Educatie" pe această linie, fiindcă oricum vom elimina acuşi, liniile respective), apoi linia cu numele zilei şi disciplinele din orarul acelei zile, apoi linia cu numele profesorilor care fac disciplinele respective:
6 7 8 9 10 ...
12:05 - 12:50 13:20 - 14:05 14:15 - 15:00 15:10 - 15:55 16:05 - 16:50 ...
7 P Grupa 1 LCH 3 D ...
Lu Istorie Limba germana Limba germana Chimie Fizica ...
Dan Ciuperca Valentina Morman/Alexandra Tudor Valentina Morman/Alexandra Tudor ...
Grupa 1 3 D ...
Ma - Limba germana Limba germana Limba germana Cultură germană ...
- Valentina Morman/Alexandra Tudor Valentina Morman/Alexandra Tudor ...
3 D 3 D Educatie 3 D ...
Mi - Matematica Biologie Educatie muzicala/Educatie vizuala ...
- Raluca Mangra Mirela Marinescu Alina Teac/Gratiela Stoian ...
Am adoptat convenţia de a separa printr-un caracter '/' numele profesorilor care fac lecţia cu câte o grupă a clasei respective (şi eventual, numele disciplinelor, pentru fiecare grupă); deasemenea, multiplicăm disciplina şi numele profesorului, când lecţia decurge pe două sau trei ore consecutive (cum avem aici pentru "Limba germana").
În unele zile, prima oră din orarul unora dintre clase (uneori şi a doua) este liberă; am introdus "-" pentru a ne semnala ulterior, acest lucru.
Nu este neapărat necesar să aliniem şi pe coloane – este suficient să ne asigurăm că itemii de pe o aceeaşi linie sunt separaţi prin câte cel puţin două spaţii (ştiind că în cadrul numelor de profesori sau discipline se foloseşte maximum un spaţiu).
Bineînţeles că dacă ar fi să aliniem totuşi pe coloane, nu am face-o manual – ci printr-un mic program care să înlocuiască în fişierul respectiv, orice secvenţă de spaţii de lungime cel puţin 2, cu câte un caracter "TAB".
Structurarea datelor din fişierele cls-*.txt
După operaţiile de editare funcţionărească descrise mai sus, toate cele 42 de fişiere cls-*.txt au câte 20 de linii, la fel structurate.
Nu ne interesează linia 2 (pe care avem "COLEGIUL..."), nici linia 4 (pe care avem intervale orare ca "7:30 - 8:15") şi nici liniile din 3 în 3 începând cu linia 5 (pe care sunt consemnate săli de clasă şi „resturi” precum "Grupa 1", sau în final "Orar generat:..."); dar nu-i necesar să eliminăm aceste linii, câtă vreme le putem doar ignora.
Totuşi n-am lucrat chiar „funcţionăreşte” (mecanic); la un moment dat am observat că profesorii dintr-un cuplaj sunt notaţi într-o ordine la o clasă şi în ordinea inversă la o altă clasă – încât, pentru a evita să avem două reprezentări distincte pentru un acelaşi cuplu, am reluat editarea manuală a fişierelor şi am adoptat ca regulă să notăm profesorii din fiecare cuplaj în ordinea alfabetică a celor două nume (deci nu "Valentina Morman/Alexandra Tudor" cum avem mai sus, ci "Alexandra Tudor/Valentina Morman").
În următorul program, funcţia txt2vct() citeşte într-un vector liniile din fişierul "cls-*.txt" indicat, reduce vectorul respectiv la cele 12 linii care ne interesează şi apoi – folosind map_dfr() şi list2DF() – constituie (pe baza liniilor de discipline şi respectiv, de profesori) şi returnează un obiect de tip data.frame care înregistrează una după alta, lecţiile existente în orar la clasa respectivă (prof | obj | zi | ora | cls):
library(tidyverse) path <- "TVtxt/" # Subdirectorul care conţine fişierele "cls-*.txt" bez <- c(2, 4, seq(5, 20, by=3)) # Liniile de ignorat txt2vct <- function(cls_txt) { con <- file(paste0(path, cls_txt)) Lines <- readLines(con, warn=FALSE) # Vector cu cele 20 de linii din 'cls-*.txt' close(con) # Reţine liniile de neignorat, elimină spaţiile iniţiale şi finale, # apoi exclude orice spaţiu intermediar de lungime mai mare ca 2 Q <- Lines[-bez] %>% # chr [1:12] str_trim(., side="both") %>% str_split(., "\\s{2,}") # Returnează 'data.frame', conţinând prof|obj|zi|ora|cls map_dfr(seq(3, 11, by=2), function(i) list2DF(list( prof = Q[[i+1]], # linia profesorilor obj = Q[[i]][-1], # linia pentru Zi şi disciplinele din acea zi zi = rep(Q[[i]][1], length(Q[[i+1]])), ora = Q[[2]][1:length(Q[[i+1]])]) ) ) %>% filter(prof != "-") %>% # fără orele libere de la începutul zilei, dacă există mutate(cls = Q[[1]]) }
Funcţiile str_trim() şi str_split() sunt vectorizate, încât le-am putut aplica „deodată”, pe vectorul în care am extras cele 12 linii.
Aplicând funcţia de mai sus (iarăşi, prin map_dfr()) pentru toate fişierele "cls-*.txt", obţinem (ca obiect data.frame) întregul orar:
TV <- map_dfr(list.files(path = path, pattern = ".txt"), txt2vct) > str(TV) 'data.frame': 1260 obs. of 5 variables: $ prof: chr "Ionela Stan-Cristache" "Alina Teac" "Iulia Salajanu" ... $ obj : chr "Educatie fizica" "Educatie muzicala" "Limba engleza" ... $ zi : chr "Lu" "Lu" "Lu" "Lu" ... $ ora : chr "7" "8" "9" "10" ... $ cls : chr "5" "5" "5" "5" ... saveRDS(TV, file = "TV-org.RDS") # setul de date corespunzător orarului original
'TV' conţine 1260 de linii ("observaţii" asupra variabilelor existente), reprezentând fiecare câte una dintre orele care se desfăşoară în cursul săptămânii în şcoala respectivă; reprezentând astfel lecţiile – prin cele 5 variabile independente între ele, prof | obj | zi | ora | cls – vom putea face uşor (angajând pachetul tidyverse) orice investigaţii sau prelucrări am dori, asupra datelor respective.
Abstractizarea numelor de profesori şi de cuplaje
Putem avea (indiferent de şcoală) trei categorii de profesori. Majoritatea au „ore proprii”, la care intră singuri la unele dintre clasele care le-au fost repartizate (şi eventual în cuplaj, la altele); pe aceştia îi vom nota prin p01, p02, p03 ş.a.m.d., în ordinea descrescătoare a numărului de ore proprii din încadrarea fiecăruia.
În cazul în care doi profesori care au ore proprii, pNN şi pMM sunt angajaţi într-un cuplaj – introducem un „profesor fictiv”, concatenând cele două nume pNNpMM şi-i alocăm lecţiile desfăşurate împreună de către cei doi.
O a treia categorie ar fi aceea (mai rară) a profesorilor „externi” – fără ore proprii, dar angajaţi în unele cuplaje; îi vom nota prin e01, e02 ş.a.m.d. şi păstrăm consemnarea prin concatenare a cuplajelor în care apar.
Pe această categorisire şi notare a profesorilor, se bazează programele din [1] pentru alocarea pe zile şi pe orele zilei a lecţiilor şi cele – pe care vrem mai încolo să le adaptăm cazului de faţă – pentru contabilizarea şi reducerea ferestrelor. Cuplajele sunt important de evidenţiat din start, fiindcă vor influenţa numărul de ore pe zi şi ferestrele fiecăruia dintre profesorii implicaţi.
Să considerăm întâi profesorii care au (şi) ore proprii:
library(tidyverse) LSS <- readRDS("TV-org.RDS") # 1260 lecţii prof|obj|zi|ora|cls DFnn <- LSS %>% filter(! grepl("/", prof)) %>% # întâi, ignorăm cuplajele count(prof, sort=TRUE) %>% # contorizează apariţiile (descrescător) mutate(pNN = c(paste0("p0", 1:9), paste0("p", 10:nrow(.)))) > str(DFnn) 'data.frame': 83 obs. of 3 variables: $ prof: chr "Diana Petculescu" "Carmen Plesa" ... $ n : int 25 24 24 24 24 21 21 21 21 20 ... # frecvenţa apariţiei $ pNN : chr "p01" "p02" "p03" "p04" ... # numele "scurte" asociate
Deci sunt 83 de profesori p01, ..., p83 care au (şi) ore proprii (la care intră singuri, nu în vreun cuplaj); unii dintre aceştia partajează (pe grupe) câte o aceeaşi clasă, cu câte un alt profesor – care fie are şi el ore proprii (deci se regăseşte între cei 83 din DFnn), fie este un profesor „extern” (fără ore proprii, angajat numai "pe grupe").
În urma editării manuale evocate mai sus, un cuplaj constă din două nume de profesori separate prin '/', în ordine alfabetică; dacă nu am fi avut grijă să le ordonăm şi să nu scăpăm vreun spaţiu înainte sau după '/' – atunci pentru separarea numelor (într-o aceeaşi ordine, pentru toate cuplajele) ar fi trebuit să folosim sort(str_trim(L[[1]])), unde L este lista returnată de strsplit() (conţinând vectorul celor două nume).
Următoarea funcţie caută numele respective în DFnn şi dacă le găseşte pe ambele, atunci notează cuplajul respectiv prin alipirea valorilor găsite în coloana $pNN – altfel, lasă numele neschimbat (acesta corespunde unui profesor „extern”):
set_cup <- function(cup) { vct <- strsplit(cup, "/", fixed=TRUE)[[1]] # vector, cu cei doi din cuplaj p1 <- DFnn %>% filter(prof==vct[1]) %>% pull(pNN) l1 <- length(p1) # este 0, dacă p1 este "extern" (fără ore proprii) p2 <- DFnn %>% filter(prof==vct[2]) %>% pull(pNN) l2 <- length(p2) if(l1 & l2) return(paste0(p1, p2)) # au şi ore proprii; notăm cuplajul prin "p1p2" if(l1) return(paste0(p1, "/", vct[2])) # cuplaj cu profesor extern if(l2) return(paste0(p2, "/", vct[1])) return(paste0(vct[1], "/", vct[2])) # ambii sunt externi (păstrăm numele) }
Angajând set_cup(), obţinem acum un tabel analog cu DFnn, pentru cuplaje:
DFcup <- LSS %>% filter(grepl("/", prof)) %>% # lecţiile cuplate count(prof, sort=TRUE) %>% mutate(pNN = "") for(i in 1:nrow(DFcup)) DFcup$pNN[i] <- set_cup(DFcup$prof[i]) # Exemplificare: print(DFcup[18:20, ]) prof n pNN 18 Catalina Enescu/Simona Ionescu 3 p76p34 19 Cristina Olaru/Elena Dragan 3 p52/Elena Dragan 20 Elena Dragan/Marcel Homorodean 3 Elena Dragan/Marcel Homorodean
În următoarea secvenţă, depistăm profesorii externi, rămaşi în coloana DFcup$pNN, le asociem numele "e01", "e02" ş.a.m.d. şi apoi renotăm în coloana DFcup$pNN (prin alipirea numelor, de exemplu "p47e01") cuplajele în care apar:
C3 <- DFcup$pNN # vectorul valorilor din coloana 3 cpx <- C3[grepl("/", C3)] # numai cuplajele cu profesor extern Pex <- unique(gsub(".*/", "", cpx)) # profesorii externi dct_x <- paste0("e0", 1:length(Pex)) names(dct_x) <- Pex # dicţionar {Prof_extern ==> eNN} # Irina Iosupescu Elena Dragan Cezar Mandle Marcel Homorodean # "e01" "e02" "e03" "e04" for(i in 1:nrow(DFcup)) { if(nchar(DFcup$pNN[i]) == 6) next vct <- strsplit(DFcup$pNN[i], "/", fixed=TRUE)[[1]] p1 <- vct[1] if(nchar(p1) > 3) p1 <- dct_x[p1] p2 <- dct_x[vct[2]] DFcup$pNN[i] <- paste0(p1, p2) } > str(DFcup) # inspectăm în consolă, structura obţinută 'data.frame': 26 obs. of 3 variables: $ prof: chr "Alina Teac/Gratiela Stoian" "Alexandra Tudor/Valentina Morman" ... $ n : int 18 10 9 9 8 6 6 6 6 5 ... $ pNN : chr "p55p71" "p82p80" "p35p77" "p47e01" ...
Avem deci 26 de cuplaje, majoritatea cu câte mai puţin de 6 ore; unele (majoritatea) angajează câte doi profesori care au şi ore proprii, unele mixează un profesor cu ore proprii şi unul extern şi avem un caz "e02e04" în care ambii profesori sunt externi.
DFnn (pentru profesorii care au ore proprii) şi DFcup (pentru cuplaje) au aceeaşi structură şi le putem reuni într-un singur „tabel”:
DFn <- DFnn %>% full_join(DFcup, by = c("prof", "n", "pNN"))
DFn are 83 + 26 = 109 linii, conţinând câte o singură dată fiecare nume de profesor sau de cuplaj din coloana $prof a setului iniţial LSS, împreună cu notaţia "pNN" sau "pNNpMM" pe care am asociat-o mai sus, numelor respective.
Problema care se pune acum (pentru a finaliza „abstractizarea numelor”) este înlocuirea pe toate cele 1260 de linii din LSS, a numelor iniţiale din coloana $prof, prin cele asociate în DFn$pNN; în mod tipic, aceasta se rezolvă în mod indirect: transformăm $prof în factor şi modificăm prin levels(), nivelele respective.
Întâi, ordonăm liniile din DFn descrescător după numărul de ore şi (în caz de egalitate) după numele din coloana $prof şi constituim un „dicţionar” (sau pentru R, vector cu nume) care împerechează numele explicite din $prof cu cele „scurte” din $pNN:
DFn <- DFn %>% arrange(desc(n), prof) dct <- DFn$pNN names(dct) <- DFn$prof # dicţionar {prof (sau cuplu) ==> notaţie scurtă}
Folosind table(), obţinem un dicţionar asemănător celui de mai sus, pentru LSS:
srt <- sort(table(LSS$prof), decreasing=TRUE) # {prof|cuplu ==> frecvenţă (nr. ore)} print(identical(names(srt), names(dct))) # TRUE
Prin identical() am verificat că dicţionarele respective conţin drept chei aceleaşi 109 nume (şi la fel ordonate).
Folosim srt (fiindcă acesta indică frecvenţa numelor din LSS) pentru a redefini LSS$prof ca factor ordonat şi în final, redenumim prin dct nivelele acestuia:
LSS$prof <- factor(LSS$prof, levels = names(srt), ordered=TRUE) levels(LSS$prof) <- dct[levels(LSS$prof)] > str(LSS) # inspectăm structura: 'data.frame': 1260 obs. of 5 variables: $ prof: Ord.factor w/ 109 levels "p01"<"p02"<"p03"<..: 3 58 8 31 45 ... $ obj : chr "Educatie fizica" "Educatie muzicala" "Limba engleza" ... $ zi : chr "Lu" "Lu" "Lu" "Lu" ... $ ora : chr "7" "8" "9" "10" ... $ cls : chr "5" "5" "5" "5" ...
Acum profesorii sunt p01, p02, ..., p83 (în ordinea descrescătoare a numărului de ore), iar cuplajele sunt reprezentate sub forma p62p34, sau p34e04, sau e02e04 (unde 'p' indică un profesor care are şi ore proprii, iar 'e' unul extern, angajat numai „pe grupe”).
Se cuvine probabil să mai precizăm că, $prof fiind acum un "factor" – intern, în LSS nu se păstrează „numele” profesorilor (accesibile separat, prin funcţia levels()), ci indecşii 1..109 ai acestora (de data aceasta, în defavoarea utilizării spaţiului de memorie – fiindcă "p01" de exemplu, ocupă 3 octeţi, în timp ce un întreg ocupă de obicei 8 octeţi).
Alte ajustări
LSS$ora este de tip character – ceea ce este neconvenabil (ora "10" ar fi aşezată înaintea orei "7", de exemplu); convertim la integer (este deja cam ridicol, să mai facem caz de utilizarea spaţiului de memorie):
LSS$ora <- as.integer(LSS$ora)
În unele programe poate fi important să avem o notaţie unitară, pentru clase; poate fi mai bine "5", decât "5A" (fiindcă "5" mai înseamnă şi că există o singură clasă a 5-a) – totuşi preferăm notaţia „standard”. Pentru a schimba în LSS numele de clasă, folosim ca şi mai sus factor() şi levels():
LSS$cls <- factor(LSS$cls) qls <- toupper(levels(LSS$cls)) # '12b' ==> '12B' qls[nchar(qls)==1] <- paste0(qls[nchar(qls)==1], "A") # '5' ==> '5A' levels(LSS$cls) <- qls
Probabil că vom reda matricea de încadrare separând cumva cele două schimburi şi vom reda clasele fiecărui schimb în ordinea nivelelor claselor (şi în ordinea literelor, pe fiecare nivel de clase).
Ţinem seama de faptul că toate clasele din primul schimb au ora '3', iar cele din al doilea au toate, ora '9' şi redefinim LSS$cls, ca factor ordonat:
schimb <- function(h) with(LSS, as.character(sort(unique(cls[ora == h])))) Sch1 <- schimb(3) Sch2 <- schimb(9) Sch1 <- c(Sch1[19:21], Sch1[1:18]) > Sch1 # inspectăm [1] "7A" "8A" "8B" "11A" "11B" "11C" "11D" "11E" "11F" "11G" "11H" "11I" [13] "12A" "12B" "12C" "12D" "12E" "12F" "12G" "12H" "12I" Sch2 <- c(Sch2[10:21], Sch2[1:9]) > Sch2# inspectăm [1] "5A" "6A" "6B" "9A" "9B" "9C" "9D" "9E" "9F" "9G" "9H" "9I" [13] "10A" "10B" "10C" "10D" "10E" "10F" "10G" "10H" "10I" LSS$cls <- factor(LSS$cls, levels = c(Sch1, Sch2), ordered = TRUE)
A fost necesar să folosim as.character() în funcţia schimb() – altfel, rezultatul returnat păstra tipul factor al câmpului LSS$cls şi modificările de efectuat apoi, se complicau.
Să mai observăm că dacă ar fi să afişăm orarul unui profesor sau al unei clase, ordonând fireşte după zile – atunci acesta ar fi redat începând cu "Jo" (nu cu "Lu"); să forţăm ordinea firească a zilelor, folosind iarăşi factor():
LSS$zi <- factor(LSS$zi, levels=c("Lu","Ma","Mi","Jo","Vi"), ordered=TRUE) saveRDS(LSS, file = "TV_lessons.RDS")
În final, am salvat LSS în fişierul "TV_lessons.RDS".
Matricea de încadrare
Matricea de încadrare se obţine imediat, ca tabelul de contingenţă a factorilor $prof şi $cls ai setului de lecţii LSS:
library(tidyverse) LSS <- readRDS("TV_lessons.RDS") # 1260 lecţii prof|obj|zi|ora|cls frm <- addmargins(table(LSS[c('prof', 'cls')])) colnames(frm) <- str_extract(levels(LSS$cls), "[A-Z]") frm[frm == 0] <- '.'
Am simplificat numele coloanelor, păstrând numai literele de clasă (în ordinea nivelelor factorului $cls) – gândindu-ne la redarea pe ecran sau pe o coală A4; redăm o imagine de ecran (parţială) a matricei, după completarea cu un antet pe care am notat nivelele de clasă corespunzătoare literelor:

Matricea de încadrare frm are 109 linii (în ordinea descrescătoare a numărului de ore), reprezentând fiecare încadrarea unui profesor sau a unui cuplu (numărul de ore la fiecare clasă şi totalul acestora); de exemplu, vedem că p55 şi p71 fac împreună (pe grupe) câte o oră la toate clasele a 9-a şi a 10-a (şi fiind notaţi cu 'p', nu cu 'e' – ei au şi ore proprii la anumite clase, apărând deci şi singuri pe câte o linie a matricei).
frm[, 1:21] ne-ar da matricea de încadrare pentru primul schimb, iar frm[, 22:42] pentru al doilea.
Subliniem că aici am ajuns la matricea de încadrare plecând de la setul dat (dedus din orarul iniţial) al tuturor lecţiilor; dar putem pune problema şi invers: dată fiind matricea de încadrare frm, să constituim setul tuturor lecţiilor prof | cls (şi să-l completăm cu $zi şi $ora, pentru a ajunge la un orar – v. [1]).
Principii, sau interese?
Dată fiind matricea de încadrare, generarea unui orar corespunzător acesteia presupune anumite configurări prealabile, sau aderarea explicită la anumite principii sau recomandări pedagogice (care ar fi de anticipat şi de luat în seamă şi de cei care decid încadrarea iniţială – alţii de obicei, decât cei care elaborează efectiv orarul).
De exemplu, în [1] am adoptat principiul repartizării în mod echilibrat (uniform) pe zile, clase, obiecte şi profesori; deci, „în principiu” – să nu avem clase, ori profesori, cu 4 ore într-o zi şi cu 7 într-o alta; lecţiile unei discipline cu cel mult 5 ore pe săptămână trebuie alocate în zile diferite (şi nu înghesuite la vreo clasă, în două zile).
Desigur, a respecta asemenea principii pedagogice şi pe de altă parte, a mulţumi toţi profesorii (ţinând seama de cerinţele justificate sau nu, ale acestora) şi a mai ţine seama eventual, de conjuncturi precum instituirea unei stări de urgenţă – sunt lucruri care de obicei, se bat cap în cap.
Desigur, unele conflicte se pot evita uşor, anticipându-le: nu încadrezi pe 5 ore la o aceeaşi clasă, un profesor extern – fiindcă atunci, profesorul respectiv ar trebui să vină la şcoală în fiecare zi pentru câte o oră (şi ar fi nemulţumit); eviţi să dai o singură clasă într-un schimb şi restul orelor în celălalt schimb – fiindcă atunci, profesorul respectiv va trebui să vină în unele zile de câte două ori (şi ar fi nemulţumit), o dată pentru orele din primul schimb şi o dată pentru cele din al doilea schimb.
Desigur, toate conflictele se pot evita simplu, dacă expui de la bun început (şi respecţi ulterior) „principiile”: îţi dau o clasă cu 5 ore – dar va trebui să le faci câte una pe zi; îţi dau şi clase din celălalt schimb – dar în unele zile vei avea probabil, ferestre între cele două schimburi („îţi dau” ţine de cel care decide asupra încadrării, în şcoala respectivă).
În cazul orarului de faţă, avem clase la care orele pe un obiect sau altul se fac toate într-o aceeaşi zi (sau în două zile); avem profesori care au 3 ore într-o zi (sau niciuna) şi 8 într-o alta; avem clase care într-o zi au 4 ore, în alta au 7 ore.
Prin urmare, cel mai probabil, generarea orarului respectiv s-a bazat nu pe ceva „principii”, ci mai degrabă pe interes: „să fie profesorii mulţumiţi”.
Când sunt profesorii mulţumiţi? Niciodată…; dar în general, ar vrea să nu aibă ferestre (nici între schimburi) şi ar dori, dacă nu vreo zi liberă (fie şi cu preţul încărcării peste măsură a vreunei alte zile), măcar jumătăţi de zi libere (adică să aibă în fiecare zi, ore numai în câte unul dintre schimburi). Putem verifica pentru orarul abordat aici, dacă tocmai de asemenea condiţii s-a ţinut seama.
Să determinăm deci numărul de ferestre şi de zile libere ale fiecăruia; dar să ne rezumăm (deocamdată) la profesorii care acoperă împreună majoritatea orelor – aceia care nu sunt angajaţi în vreun cuplaj (pentru cei angajaţi în cuplaje, calculul ferestrelor devine mai complicat, trebuind vizate orele proprii ale tuturor celor cu care este cuplat fiecare, precum şi orele cuplajelor respective).
Întâi, extragem din LSS lecţiile celor care nu intră în vreun cuplaj; plecăm de la vectorul celor 109 nume din $prof, separăm cuplajele (sunt 26), evidenţiem cele câte două părţi ale cuplajelor (neglijând apariţiile multiple) şi în final, ignorăm din LSS lecţiile corespunzătoare cuplajelor şi părţilor acestora (obţinând setul LSS1):
VP <- levels(LSS$prof) # chr [1:109] "p01" "p02" "p03" "p04" ... CUP <- VP[nchar(VP) > 3] # chr [1:26] "p55p71" "p82p80" "p35p77" "p47e01" ... split_twin <- function(cup) # extrage profesorii dintr-un cuplaj (v. [1]) strsplit(cup, "(?<=.{3})", perl=TRUE)[[1]] inCUP <- map(CUP, split_twin) %>% unlist() %>% unique() # chr [1:25] "p55" "p71" "p82" "p80" "p35" ... LSS1 <- LSS %>% filter(! prof %in% union(CUP, inCUP)) %>% droplevels() # lecţiile celor care nu intră în vreun cuplaj > str(LSS1) 'data.frame': 948 obs. of 5 variables: $ prof: Ord.factor w/ 62 levels "p01"<"p02"<"p03"<..: 3 29 41 12 12 29 ... $ obj : chr "Educatie fizica" "Matematica" "Istorie" "Limba franceza" ... $ zi : Ord.factor w/ 5 levels "Lu"<"Ma"<"Mi"<..: 1 1 1 2 2 2 2 3 3 3 ... $ ora : int 7 10 11 8 9 10 12 9 10 11 ... $ cls : Ord.factor w/ 42 levels "7A"<"8A"<"8B"<..: 22 22 22 22 22 22 ...
Desigur, am avut grijă să excludem – prin droplevels() – din „noul” factor LSS1$prof, nivelele cuplajelor şi părţilor acestora (şi ne-au rămas 62 de profesori).
Să observăm că LSS1 conţine o parte semnificativă (948, adică vreo 75%), a celor 1260 de lecţii iniţiale (încât observaţiile pe care le vom face pentru LSS1 sunt suficient de credibile şi pentru întregul set LSS).
Următoarea funcţie determină (în cel mai simplu mod) numărul zilnic de ferestre ale unui profesor din LSS1:
gaps_in_day <- function(P) LSS1 %>% filter(prof == P) %>% split(.$zi) %>% # lista pe zile, a orelor profesorului map(., function(Z) # determină numărul de ferestre din zi ifelse(nrow(Z) > 0, diff(range(Z$ora)) + 1 - nrow(Z), NA) ) %>% unlist() # vector cu numărul zilnic de ferestre (NA = zi liberă)
Z fiind setul lecţiilor profesorului P dintr-o anumită zi, diff(range(Z$ora)) dă diferenţa dintre rangul ultimeia şi rangul primeia dintre cele nrow(Z) ore – de unde, formula de calcul a numărului de ferestre conţinută mai sus (desigur, dacă nrow(Z) este 0, atunci P este liber în acea zi). Subliniem în treacăt că dacă P ar face parte dintr-un cuplaj, atunci calculul ferestrelor sale se complică, trebuind avute în vedere şi orele acelui cuplaj (şi încă, orele altor cuplaje care depind de P).
Nu rămâne decât să aplicăm gaps_in_day() tuturor profesorilor din LSS1:
Gap <- map(levels(LSS1$prof), gaps_in_day) names(Gap) <- levels(LSS1$prof) # listă {Prof ==> vectorul de ferestre zilnice} Gap <- list2DF(Gap) # transformă lista în 'data.frame' Gap[6, ] <- addmargins(table(LSS1[c("prof","cls")]), 2)[, 43]
Am adăugat o a 6-a linie, conţinând totalul orelor profesorilor respectivi (înscrişi în Gap descrescător după acest total); ilustrăm rezultatul, pentru primii 20:
> Gap[, 1:20] p01 p02 p03 p04 p05 p06 p07 p09 p10 p11 p12 p13 p14 p15 p16 p17 p18 p19 p20 p21 1 1 0 0 1 0 NA 0 1 0 0 0 0 0 0 0 1 0 0 NA NA 2 0 1 NA 0 0 0 0 0 NA 0 0 0 0 NA 0 1 0 0 1 0 3 0 0 0 NA 1 0 0 0 0 0 0 0 0 0 0 NA 0 1 0 0 4 0 0 0 1 0 0 0 NA 0 0 0 0 0 0 0 0 1 0 0 1 5 NA 0 0 0 0 0 0 0 0 0 0 0 NA 0 0 1 0 NA 0 0 6 25 24 24 24 24 21 21 21 20 20 20 20 20 20 19 18 18 18 18 18
De exemplu, p01 are o singură fereastră (în ziua "Lu") şi are o zi liberă ("Vi").
Constatăm că o bună parte dintre profesorii care au multe ore (cel puţin 18, adică în primele vreo 30 de coloane) au totuşi câte o zi liberă; marea majoritate au câte cel mult o singură fereastră (exceptând vreo două cazuri; de exemplu, p17 are trei ferestre).
Putem constata imediat câte ferestre avem pe fiecare zi şi câţi profesori liberi:
ngp <- sapply(1:5, function(z) sum(Gap[z, ], na.rm=TRUE)) # 6 4 9 6 6 (total, 31 ferestre) nfr <- sapply(1:5, function(z) sum(is.na(Gap[z, ]))) # 19 16 15 16 19 (liberi/zi)
Deci în total, la profesorii neangajaţi în cuplaje avem 31 de ferestre, însemnând 3.27% dintre cele 948 de ore ale acestora – ceea ce este chiar remarcabil, dacă facem abstracţie de „înghesuirea” orelor (prin care s-a obţinut reducerea ferestrelor şi apariţia de zile libere pentru cei cu multe ore).
Nu ne mai interesează aici să vedem lucrurile şi pe fiecare schimb în parte – verificând de exemplu, proporţia celor care, fiind încadraţi pe clase din ambele schimburi, îşi fac orele în câte un singur schimb pe zi (exceptând poate o singură zi, în care ar avea ore în ambele schimburi, dar fără ferestre); este de aşteptat ca această proporţie să fie mare (ceea ce este iarăşi, remarcabil), dat fiind că numărul total de ferestre este mic.
Descoperirea cuplajelor de clase
Doar consultând fişierul PDF de la care am plecat este greu să-ţi dai seama dacă există clase cuplate – două clase care într-o aceeaşi zi şi oră trebuie despărţite în câte două grupe din care, combinând o grupă a uneia cu o grupă a celeilalte, rezultă două noi clase, la care trebuie să intre câte un anumit profesor; celor doi profesori implicaţi trebuie să li se repartizeze clasele respective în câte o aceeaşi zi şi oră – încât evidenţierea din start a cuplajelor de clase devine foarte importantă.
Cel mai probabil (în absenţa unor precizări explicite), dacă există clase cuplate – acestea trebuie căutate la cuplajele de profesori: ştim de mai sus că lecţiile de "Educatie muzicala/Educatie vizuala" (şi bună parte a celor de "Informatica", sau limbi străine) se desfăşoară „pe grupe”; este posibil să se combine într-o aceeaşi zi şi oră, câte o grupă de la clasa 9A cu câte una de la 9B să zicem, iar la cele două clase „noi” să intre profesorul de muzică, respectiv cel de "Educatie vizuala" – economisând o oră: în loc să facă fiecare cu câte o jumătate de clasă, face fiecare cu câte o clasă întreagă (altfel spus, totalul rezultat mai sus de 1260 de lecţii, trebuie diminuat).
Condiţia ca un cuplaj de profesori să lucreze nu pe câte o grupă a clasei, ci pe clase întregi, rezultate prin combinarea grupelor a două clase – este apariţia de două ori într-o aceeaşi zi şi oră, a acelui cuplaj:
> LSS %>% filter(nchar(as.character(prof)) > 3) %>% group_by(prof, zi, ora) %>% count() %>% filter(n > 1) # reţinem numai apariţiile duble (triple, dacă există) # A tibble: 9 x 4 Groups: prof, zi, ora [9] prof zi ora n 1 p55p71 Ma 8 2 2 p55p71 Ma 9 2 3 p55p71 Ma 10 2 4 p55p71 Mi 7 2 5 p55p71 Mi 8 2 6 p55p71 Mi 9 2 7 p55p71 Mi 10 2 8 p55p71 Jo 8 2 9 p55p71 Jo 9 2
Deci avem 9 perechi de clase care cuplează în câte o aceeaşi zi şi oră, în sarcina aceloraşi doi profesori (p55 şi p71); altfel spus, avem în total nu 1260 de „lecţii”, ci numai 1251. Amintindu-ne că avem 9 clase a 9-a şi 9 clase a 10-a, care fac fiecare "Educatie muzicala/Educatie vizuala" – putem constata care sunt cele 9 cuplaje de clase:
> LSS %>% filter(obj=="Educatie muzicala/Educatie vizuala") %>% select(-obj) %>% arrange(prof, zi, ora, cls) prof zi ora cls prof zi ora cls prof zi ora cls 1 p55p71 Ma 8 9H 7 p55p71 Mi 7 9B 13 p55p71 Mi 10 9D 2 p55p71 Ma 8 10C 8 p55p71 Mi 7 10D 14 p55p71 Mi 10 10G 3 p55p71 Ma 9 9C 9 p55p71 Mi 8 9F 15 p55p71 Jo 8 9G 4 p55p71 Ma 9 10B 10 p55p71 Mi 8 10E 16 p55p71 Jo 8 10I 5 p55p71 Ma 10 9I 11 p55p71 Mi 9 9A 17 p55p71 Jo 9 9E 6 p55p71 Ma 10 10H 12 p55p71 Mi 9 10A 18 p55p71 Jo 9 10F
Constatăm că fiecare clasă a 9-a este cuplată cu câte o clasă a 10-a (oarecum surprinzător – de regulă se cuplează clase de acelaşi nivel; dar constatarea făcută se confirmă uşor, consultând orarele claselor respective din fişierul PDF original).
De exemplu, în ziua Ma, ora 8 – p55 intră la clasa constituită din grupele 1, iar p71 intră la clasa constituită din grupele 2, ale claselor 9H şi 10C.
Desigur, ar fi acum de corectat matricea de încadrare – trecând clasele a 9-a la p55, clasele a 10-a lui p71 şi eliminând apoi, cuplajul p55p71; va trebui apoi, să avem grijă să repartizăm în câte o aceeaşi zi (şi apoi, în câte o aceeaşi oră a zilei) perechile de clase cuplate (ca 9H şi 10C) acestor doi profesori.
Repartizarea uniformă a lecţiilor…
Acum avem pregătită, matricea de încadrare – completată faţă de forma standard (care vizează numai profesorii propriu-zişi, reali) prin adăugarea de „profesori-fictivi” (reprezentând cuplajele de profesori la câte o aceeaşi clasă) şi corectată (cum tocmai am indicat, mai înainte) pentru a reflecta şi cuplajele de câte două clase.
Putem deci constitui listele desemnate în [1] prin (de la twins) Tw1, Tw2 şi Twx – în care memorăm pe categorii, cine de cine depinde la alocarea pe zile şi apoi, pe orele zilei – şi putem fixa pe zile (în lista denumită şi ea, TwCl) anumite lecţii (după cum ne convine), între care neapărat pe cele prevăzute pe cuplajele de clase.
După aceasta – vom putea aplica pe setul de date prof | cls corespunzător matricei de încadrare, programele de repartizare echilibrată pe zile şi apoi, pe orele zilei, pe care le avem deja în [1].
… dar asta-i deja o altă poveste!
vezi Cărţile mele (de programare)