"I", "II", iată și "III"; de regulă, nu termini niciodată.

Unde se află și care sunt, punctele de inflexiune ?

De fapt, întrebarea ar fi întâi ce sunt "inflexiunile"… În cazul de față par suficiente vederile comune (bătătorite mai pe deasupra, în liceu): constatasem că într-un anumit caz, în primul cadran $\boldsymbol\Gamma$ urcă (având $f'(x)\gt 0$) spre cel mai înalt punct, întâi convex (cu $f''(x)\gt 0$) și de la un moment încolo, concav (cu $f''(x)\lt 0$) — deci are neapărat un "punct de inflexiune" (când $f''(x)=0$); iar în [3] l-am depistat numeric, pășind puțin câte puțin din origine spre punctul maxim și testând mereu semnul derivatei a doua în punctul curent (mai precis… am lăsat calculatorului să-l depisteze, de la caz la caz).

Pe vremuri, începând de pe la Descartes, Newton, Leibnitz și Bernoulli până pe la 1900 și ceva, teoria curbelor plane era la mare preț; astăzi… ce-ți mai trebuie, poți cere calculatorului să-ți găsească numărul și să-ți vizualizeze în fel și chip contextul acestuia (păi nu? dacă ai toate cele de-a gata… mai pasă cuiva cum de merg lucrurile?)

Încercăm totuși să găsim expresia simbolică (nu aproximată numeric de la caz la caz) a inflexiunilor lui $\boldsymbol\Gamma$ (…făcând abstracție de ideea avangardistă că odată și odată ne vom îmbogăți așa de mult încât calculatorul ne va putea scuti și de asemenea încercări).

Reluăm ecuația curbelor Cassini de focare $\boldsymbol{\pm(a, 0)}$, cu $\boldsymbol{a \lt b \lt a\sqrt{2}}$:

Din expresia cu derivate parțiale a lui $\boldsymbol{f''(}x,\,y=f(x)\boldsymbol{)}$ (v. [1]), avem (neglijând numitorul) ecuația $\boldsymbol{F_x^2F_{yy} + F_y^2F_{xx} - 2F_xF_yF_{xy} = 0}$, reprezentând o curbă care trece prin punctele de inflexiune ale funcției implicite $F(x,y)$.
Obs. Am scris prudent "o curbă" și nu "una sau mai multe curbe"…
"Teorema funcțiilor implicite" se referă la un punct, afirmând în condițiile cunoscute, existența și unicitatea unei funcții $f$, pe o vecinătate a punctului respectiv (încât $f$ să aibă proprietățile specificate în teoremă, privitoare la $f'$ și $f''$) — de aceea pare prudent să zicem mai sus "o curbă". Dar de fapt… prin punctele de inflexiune trec mai multe curbe! (și poate ar fi de elucidat dacă sau în ce condiții și măsură, acestea "coincid" pe câte o vecinătate a punctelor de inflexiune). De!… "teoria" tratează ce trebuie tratat, nu spune chiar totul.

Pentru $\boldsymbol\Gamma$, ecuația $f''=0$ revine (mot-à-mot) la:

Dar… să ne convingem că este așa! (adică… să vedem pe ecran. Păi nu? azi, ca să te convingi e destul dacă "vezi pe sticlă"). Pentru aceasta, adăugăm în programul "2512b.R" (v. [3]) o secvență care imită pe cea din jurul funcției anterioare bern():

V <- 4*div_x(1000)
W <- 4*div_y(1000)
bern_pq <- function(x, y) {  # modelează ecuația (2)
    p <- x^2 + y^2 - a^2
    q <- x^2 + y^2 + a^2
    x^2*p^2*(q+2*y^2) + y^2*q^2*(p+2*x^2) - 4*x^2*y^2*p*q
}    
Z <- outer(V, W, bern_pq)
contour(V, W, Z, levels = 0, drawlabels = FALSE, add = TRUE, col="blue")

Figura ne arată că ecuația (2) reprezintă o curbă care se suprapune celeia găsite "empiric" în [3] (de unde au rămas pe grafic punctele de inflexiune ale lui $\boldsymbol\Gamma$, prin care vedem acum că trece și curba de ecuație (2)); în [3] am citat (de prin cărțile vechi) că această curbă reprezintă "locul inflexiunilor curbelor $\boldsymbol\Gamma$ omofocale" și că acest loc "este o lemniscată Bernoulli":

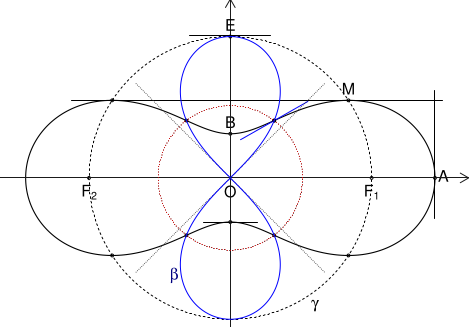
Credem noi ochilor, dar este cam surprinzător ceea ce a reieșit din figură, că (2) reprezintă aceeași curbă ca și (3) — surprinzător, fiindcă expandând (2) se obține o ecuație de gradul 8 și aceasta… parcă nu se "reduce", nicidecum, la (3).
Într-adevăr, forma mot-à-mot din (2) echivalează cu:

și avem $(\mathrm{p}-\mathrm{q})^2=4a^4$, $\mathrm{pq}=(x^2+y^2)^2-a^4$, iar $x^2\mathrm{p} + y^2\mathrm{q}=(x^2+y^2)^2 - a^2(x^2-y^2)$; deci (2) revine (direct, fără aranjări de monoame) la această ecuație:

Dar să nu ne gândim acum, la "reducerea" ecuației (4) la forma $(\boldsymbol{\beta})$… Coordonatele punctelor de inflexiune sunt soluțiile sistemului de ecuații (1) și (4).

Pentru calcul, pare convenabil să exprimăm ecuațiile respective în coordonate polare, $x=r\cos\theta,\,y=r\sin\theta$; astfel, $x^2+y^2=r^2$, $x^2-y^2=r^2\cos 2\theta$ și $2xy = r^2\sin 2\theta$ iar sistemul devine:

Din prima ecuație scoatem

Rezultă $\sin^2 2\theta = 1-\cos^2 2\theta = \dfrac{4a^4r^4 - (r^4+a^4-b^4)^2}{4a^4r^2}$, iar a doua ecuație devine:

Ne bucurăm să putem lăsa restul calculelor în seama lui SageMath:

sage: var('r,a,b')
sage: H = (r^4-a^4)*(r^4+b^4-a^4) + 4*a^4*r^4 - (r^4+a^4-b^4)^2
sage: expand(H).factor()
(a^4 - b^4 + 3*r^4)*b^4

Rezultă că

adică punctele de inflexiune se află pe cercul $x^2+y^2 = \sqrt{\frac{b^4-a^4}{3}}$.

Din (6) avem $\theta = \frac{1}{2}\arccos\frac{r^4+a^4-b^4}{2a^2 r^2}$ ceea ce duce la următoarea secvență de comenzi, pentru a adăuga pe graficul de mai sus punctele de inflexiune (și ne convingem că se suprapun peste cele plotate anterior, semn că n-am greșit la calcule):

R <- sqrt((b^4-a^4)/3)  # pătratul razei
fi <- acos((R^2+a^4-b^4)/(2*R*a^2)) / 2  # unghiul polar
x1 <- sqrt(R) * cos(fi)  # pentru inflexiunea (x1,y1) din primul cadran
y1 <- sqrt(R) * sin(fi)
points(c(x1, x1, -x1, -x1), c(y1, -y1, y1, -y1), 
       pch=19, cex=0.7, col="red")

Pe de altă parte, exprimând $\cos\theta$ din (6), putem explicita coordonatele inflexiunii din primul cadran (celelalte rezultă prin simetrie față de axe):

Ținând seama de (6) și (8), avem: $\boldsymbol{r^2+a^2\cos 2\theta =}$
$=r^2 + a^2\dfrac{r^4+a^4-b^4}{2a^2r^2}=\dfrac{3r^4+a^4-b^4}{2r^2}=\dfrac{1}{2r^2}\left(3\dfrac{b^4-a^4}{3}+a^4-b^4\right)\boldsymbol{=0}$
și fiindcă $r^2+a^2\cos 2\theta=0$ este forma polară a ecuației (3), rezultă că punctele $(\pm x_1,\,\pm y_1)$ se află pe $\boldsymbol\beta$. Fiindcă în (3) nu apare explicit decât $a$ — rezultă că lemniscata Bernoulli cu ecuația (3) trece prin punctele de inflexiune ale tuturor ovalelor Cassini omofocale, pentru care $a \lt b \lt \sqrt{2}\,a$.

La sfârșit, merită subliniat probabil, că această proprietate este demonstrată (în cărțile vechi, desigur) folosind ingrediente specifice geometriei diferențiale — v. de exemplu, THE Theory of plane curves (Surendra Mohan Ganguli, University of Calcutta, 1925), Volume II, pag. 264-265 (itemul nr. 213 "POINTS OF INFLECTION").
Mai sus avem în sfârșit, o demonstrațiune elementară.

Dar, cum am mai spus "nu termini niciodată". Să observăm că scăzând (3) din (4), rezultă încă o curbă importantă, de trece prin punctele de inflexiune ale lui $\boldsymbol\Gamma$ — anume o hiperbolă echilateră; nu mai redăm aici ecuația acesteia, dar reproducem figura finală, reflectând și acest fapt:

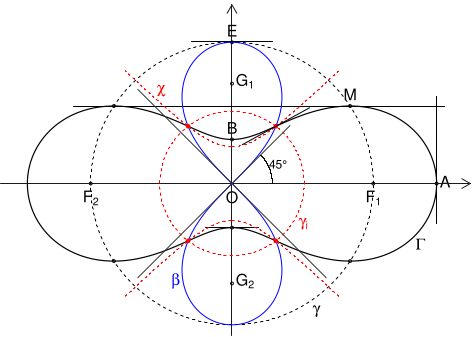
"Legenda" recapitulativă a figurii ar fi următoarea:
—($\boldsymbol{l1}$) Curba etichetată cu $\boldsymbol\Gamma$ reprezintă o curbă Cassini, cu focarele $F_{1,2}=\pm(a, 0)$, în cazul $a\lt b \lt a\sqrt{2}$.
—($\boldsymbol{l2}$) Cercul $\boldsymbol\gamma$ cu $F_1F_2$ ca diametru, trece și prin cele 4 puncte cel mai depărtate de axa orizontală (punctele "maxime" ale lui $\boldsymbol\Gamma$); fiindcă ecuația $(\boldsymbol\gamma):\,x^2+y^2=a^2$ nu implică și parametrul $b$, rezultă că toate cassinienele vizate în $(l1)$ care au aceleași focare, își au "maximele" pe cercul $\boldsymbol\gamma$.
—$(\boldsymbol{l3})$ Curba colorată "blue" și etichetată cu $\boldsymbol\beta$ este o lemniscată Bernoulli, cu focarele $G_{1,2}=\pm\left(0,\,\dfrac{a}{\sqrt{2}}\right)$ și conține punctele de inflexiune ale tuturor cassinienelor omofocale din $(l1)$ (dar pe figură am redat o singură curbă $\boldsymbol\Gamma$; am marcat inflexiunile prin puncte roșii ceva mai mari și am dus o bucată de tangentă la $\boldsymbol\Gamma$, într-unul dintre punctele sale de inflexiune; am trasat și bisectoarele sistemului de axe, care sunt tangente lemniscatei în vârful acesteia).
—$(\boldsymbol{l4})$ Cercul roșu, marcat nu prea inspirat cu $\boldsymbol{\gamma_i}$, trece și el, prin punctele de inflexiune, dar raza lui depinde și de $b$.
—$(\boldsymbol{l5})$ Curba roșie $\boldsymbol{\chi}$ este o hiperbolă echilateră care are ca asimptote bisectoarele sistemului de axe și care, trece deasemenea prin punctele de inflexiune ale lui $\boldsymbol\Gamma$ (dar ecuația ei depinde și de $b$).

Destul!… Dar dacă nu ne-ar prinde iarna (care iarnă? doar colindătorii), am încerca să redăm pe figură și curba care conține centrele cercurilor osculatoare în punctele lui $\boldsymbol\Gamma$ (bine… tot n-am termina: [2] sugerează încă ceva, chiar interesant, de spus).