Din raţiuni pedagogice –inducând cumva şi tendinţa naturală de "poetizare"– întrebuinţăm uneori exprimări simplificate, pentru diverse rezultate matematice. De exemplu, se foloseşte formularea orală "logaritmul produsului este suma logaritmilor", sau (cum am scrie la tablă) log Π = ∑ log; desigur, o exprimare mai precisă şi mai plină de substanţă ar fi: $\;\left(\mathbb{R_+^{\ast}},\,\cdot\right){\lower 3pt\ln\atop\raise 2pt \simeq}\left(\mathbb{R},\,+\right)$. Pentru prima dintre cele două "mnemonice" avem de subânţeles din context despre ce vorbim (funcţie logaritmică de bază dată, aplicată unui produs finit de numere pozitive); cea de-a doua nu mai necesită un context explicativ (ci "doar" unul cognitiv) - dat fiind că implică notaţii matematice standardizate (în baza cărora ea se citeşte direct: grupul multiplicativ al numerelor reale strict pozitive este izomorf, prin funcţia "logaritm natural", cu grupul aditiv al numerelor reale).

Am demonstrat anterior (v. [1]) că funcţia complexă $f(z)=\sqrt{z\,},\,z\in\mathbb{C}$ transformă un cerc care trece prin origine într-o lemniscată Bernoulli (a cărei axă are direcţia înjumătăţită faţă de direcţia diametrului prin origine al cercului). Formularea simplificată ar fi: "radicalul unui cerc care trece prin origine este o lemniscată Bernoulli", iar ca reprezentare mnemonică (angajând simboluri matematice existente) am putea adopta $\boxed{\sqrt{\circlearrowright}\,\leadsto\,\infty}\,$ - ştiind că lemniscata Bernoulli seamănă cu simbolul pentru "infinit" şi convenind că simbolul $\circlearrowright$ sugerează o traiectorie circulară care pleacă din origine (deci un cerc care trece neapărat, prin origine).

Când scrii "la tablă" poţi exploata capacităţile proprii de invenţie verbală şi picturală, în scopul de a lămuri sau sintetiza o chestiune sau alta (de exemplu, la tablă aş fi desenat lemniscata tot ca un simbol "infinit", dar subţiat şi rotit faţă de orizontală). Însă într-un "mediu electronic" eşti oarecum restricţionat, trebuind să descoperi şi să foloseşti limbajele şi facilităţile pachetelor software.

În MathJax (de care ne folosim aici) putem obţine formula de mai sus (cu simbolul "infinit" rotit) prin următoarea secvenţă (care pentru a deveni operaţională, trebuie marcată la început şi sfârşit cu simbolul "dollar"; comentariile –marcate cu "%", ca în TeX– trebuie eliminate):

 \boxed{
    \sqrt{\circlearrowright}    %% $\sqrt{\circlearrowright}$
    \leadsto    %% $\leadsto$
    {\style{transform:rotate(20deg)}{\infty}}    %% $\style{transform:rotate(20deg)}{\infty}$
 }
%% $\boxed{\sqrt{\circlearrowright}\leadsto{\style{transform:rotate(20deg)}{\infty}}}$   radicalul cercului este o lemniscată Bernoulli (rotită)

Am folosit aici comanda \style, inventată de MathJax pentru a stila CSS o formulă (de exemplu, aplicându-i o anumită culoare sau ca aici, o anumită transformare); însă rezultatul depinde de browserul care va deschide documentul (recunoaşte proprietatea CSS transform?).

Este de observat şi că simbolul standard $\infty$ este elegant, având o porţiune trasată mai gros decât cealaltă (ceea ce desigur că "la tablă" am putea evita); aceasta perturbă însă, asemănarea dorită cu o lemniscată (curbă care ar trebui trasată omogen ca grosime).

Suntem deci în faţa unor noi probleme (şi avem noi deschideri de investigat): cum putem crea un nou simbol matematic, încât să-l putem accesa din LaTeX –şi eventual, din MathJax– la fel cum accesăm simbolurile existente?

Deocamdată, "ne punem în temă" şi improvizăm aici nişte soluţii parţiale.

Pentru simboluri simple, putem folosi imediat anturajul {picture} din LaTeX (nu este nevoie să includem vreun pachet grafic):

\documentclass[a4paper, 12pt]{article}
\newcommand\circleByOrig{
    \setlength{\unitlength}{1em}
    \vcenter{\hbox{
                \begin{picture}(0.7, 1.2) (0.2, 0)
                    \put(0.5, 0.5){\circle{1}}
                    \linethickness{.2pt}
                    \put(-0.2, 0.5){\vector(1, 0){0.9}}
                    \put(0, 0.2){\vector(0, 1){1.05}}
                \end{picture}
            }
    }
}
\begin{document}
    \Large{$\sqrt{\circleByOrig}$}
\end{document}

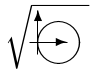
În preambulul documentului am instituit o nouă comandă (pe care am denumit-o cam pompos \circleByOrig{}); prin comenzile încorporate ei se "desenează" un cerc care trece prin originea sistemului de axe (doar că în cea mai banală poziţie: cerc tangent în origine axei verticale). În {document}, am folosit comanda respectivă în "modul math", sub \sqrt (apoi am mărit graficul, prin \Large; dar pe imaginea redată mai sus am dublat mărimea rezultată).

Eludăm aici, aspectele banale: cum se instalează LaTeX, pe o platformă sau alta; un document LaTeX începe de regulă cu alegerea unuia dintre formatele prestabilite (aici, article), poate conţine apoi un "preambul" (unde se pot defini sau redefini comenzi) şi apoi urmează conţinutul propriu-zis (sub \begin{document}). Un document LaTeX se scrie folosind un editor de text obişnuit, rezultând un fişier denumit cu extensia ".tex"; compilând acest fişier cu xelatex, obţinem (direct) fişierul ".pdf" - forma finală a documentului (gata de tipărit sau de vizualizat).

Fişierul .tex conţine atât textul care va constitui conţinutul propriu-zis al documentului, cât şi comenzi de secţionare şi formatare a acestuia. La începutul compilării nu interesează decât aspectele metrice: fiecărui caracter îi este asociată câte o boxă dreptunghiulară (ale cărei dimensiuni sunt preluate din formatul de bază declarat prin \documentclass); fiecărui cuvânt îi este asociată câte o boxă (juxtapunând boxele asociate literelor componente şi aliniind orizontal "punctele de referinţă" ale acestora) şi fiecărei linii de text îi corespunde boxa rezultată din lista boxelor cuvintelor acesteia. Fiecărui grup de linii de text consecutive nevide (numit "paragraf"), îi este asociată o boxă verticală, apoi acestea sunt înlănţuite pe verticală pentru a constitui o pagină (ca boxă verticală dimensionată corespunzător formatului de bază ales).

În mod implicit, spaţiul dintre cuvintele care compun un paragraf este reglat dinamic (implicând eventual şi despărţirea în silabe, conform unui "dicţionar" prealabil) astfel încât liniile de text (exceptând eventual, ultima linie a paragrafului) să aibă în final o aceeaşi lungime grafică (dată de lăţimea paginii, pentru formatul ales).

În final –după structurarea metrică evocată mai sus– codurile interne ale caracterelor sunt mapate pe fontul (sau "setul de caractere") implicit (sau explicitat în preambul), încât boxele constituite sunt "umplute" cu formele grafice corespunzătoare (rezultând ".pdf"-ul obişnuit).

În cadrul comenzii \circleByOrig am specificat întâi (prin \setlength) unitatea de măsură (anume 1 em) pentru valorile numerice care urmează în corpul comenzii. Primul parametru al mediului {picture} indică lăţimea (0.7em) şi înălţimea (1.2em) boxei în care urmează să fie desenat caracterul; bineînţeles că iniţial, am ales o lăţime mai mare (de 1.2em) - dar aşa, bara orizontală a simbolului "radical" (vezi imaginea) se întindea (inutil) cât să acopere această lăţime (boxa asociată radicalului fiind implicit corelată cu boxa asociată simbolului conţinut de acesta).

Prin al doilea parametru din {picture} am specificat coordonatele pentru "punctul de referinţă" al desenului; dacă nu-l specificam –cum am şi făcut iniţial– atunci acesta ar fi fost implicit (0, 0) - dar aşa, cercul ar fi fost prea apropiat de bara oblică a radicalului; prin urmare, am deplasat originea spre dreapta, alegând (0.2, 0). Alinierea corectă a simbolului construit faţă de boxele "vecine", necesită ambalarea într-o boxă orizontală (\hbox) centrată pe verticală (prin \vcenter).

Construcţia propriu-zisă este simplă; \put(0.5,0.5){\circle(1)} trasează cercul de diametru 1em având centrul în punctul (0.5em, 0.5em); \put(-0.2,0.5){\vector(1,0){0.9}} trasează vectorul cu direcţia (1,0) (deci, orizontal) de lungime 0.9em, având originea în punctul (-0.2em, 0.5em) (dar n-am mai aflat o modalitate simplă pentru a subţia săgeţile respective).