Orar pe o școală fără profesori (III)
[1] Orar pe o școală fără profesori (II)
[2] V.Bazon - De la seturi de date și limbajul R, la orare școlare (Google Books)
[3] V. Bazon - Orare școlare echilibrate și limbajul R (Google Books)
Inventarea profesorilor (partea a doua)
Am văzut în [1] că încadrarea profesorilor pe o anumită disciplină este dată de o colorare a grafului claselor care nu pot fi atribuite unui aceluiași profesor; am inventat astfel, prin programul enframe.R, o încadrare pe disciplina "Fi", compatibilă cu valorile zl|ora din orarul "pe clase" (fără profesori) de la care plecasem.
În enframe.R tăiem (comentăm) linia care definea ORR și considerăm acum o altă disciplină, angajând ultimul set ORR (în care înscrisesem profesorii de "Fi"):
> ORR <- readRDS("orar-cl_5.RDS") > Discip <- "Bi" > source("enframe.R")
Pentru "Biologie" obținem graful următor, cu o 3-colorare care induce încadrarea vp redată și ea mai jos:
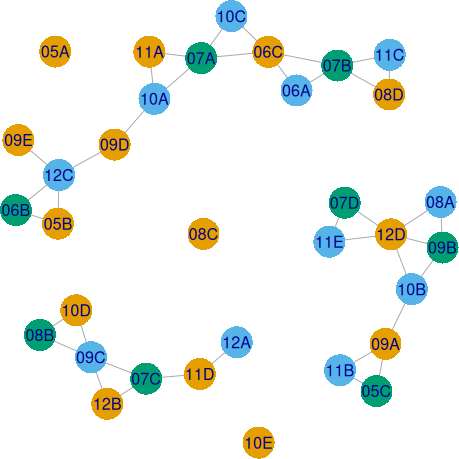
> vp # încadrarea propusă pentru 'Bi' $Bi1 "05A" "05B" "06C" "08C" "08D" "09A" "09D" "09E" "10D" "10E" "11A" "11D" "12B" "12D" # orange $Bi2 "06A" "08A" "09C" "10A" "10B" "10C" "11B" "11C" "11E" "12A" "12C" # magenta $Bi3 "05C" "06B" "07A" "07B" "07C" "07D" "08B" "09B" # green
Cele nrow(ZH) =55 ore de "Bi" au fost repartizate astfel:
> frh <- table(ZH$cls) > sapply(vp, function(P) sum(frh[P])) Bi1 Bi2 Bi3 21 20 14
Putem muta niște clase de la Bi1 și Bi2, la Bi3:
> could_move(1,3) [1] "05A" "08C" "09D" "09E" "10E" > could_move(2,3) [1] "12A"
De altfel, se vede și pe desenul redat mai sus că de exemplu, putem schimba culoarea lui 12A din magenta în green (fiindcă 12A nu are adiacenți green) — ceea ce echivalează cu a trece 12A de la Bi2 la Bi3.
Alegem să mutăm 09D (cu 2 ore), 09E (cu o oră) și 12A (cu o oră) — rezultând distribuția echilibrată 18 19 18. Înscriem încadrarea vp rezultată astfel, în ORR:
ORR <- ORR %>% rowwise() %>% mutate(prof = ifelse(obj %in% Discip, prof_to(cls), prof)) %>% ungroup() > table(ORR$prof) # verificare Bi1 Bi2 Bi3 Fi1 Fi2 Fi3 Fi4 Fi5 896 18 19 18 18 18 18 18 3 > saveRDS(ORR, "orar-cl_5.RDS")
Dar oare, putem proceda tot așa de simplu ca în cele două cazuri tratate mai sus (Fi și Bi), pentru oricare disciplină de pe cele 896 lecții rămase ?
(III) trebuie 7, nu 9, profesori de "Mt"
Pe "Matematică" avem în total nrow(ZH)=137 lecții (cam cât aveau împreună "Fi" și "Bi"), iar clasele au 4 sau 5 ore de "Mt" (nu una-două fie 3, ca în cele două cazuri anterioare) — așa că este de așteptat ca "Mt" să fie mai complicat de tratat…
Pentru Discip=Mt, enframe.R din [1] ne propune o încadrare vp cu 9 profesori:
Mt1 Mt2 Mt3 Mt4 Mt5 Mt6 Mt7 Mt8 Mt9
20 18 17 21 15 17 17 8 4
În loc să vedem (folosind could_move(), ca mai sus) ce clase mai putem muta între ei, încât să echilibrăm încadrarea respectivă, să observăm că:
> clique_num(G) [1] 7 # ordinul maxim al clicilor lui G
însemnând că trebuie „inventați” (cel puțin) 7 profesori de "Mt"; deci numărul ideal ar fi 7, sau poate 8 — dar nu 9, câți au rezultat în vp…
9-colorarea furnizată de igraph::greedy_vertex_coloring() pentru graful G, nu pare a fi, de data aceasta, optimă (cu număr minim posibil, de culori).
Dar se știe că există o ordine de parcurgere a vârfurilor, pentru care metoda greedy produce o colorare optimă. Deci dacă repetăm colorarea, asumând diverse ordonări prealabile de vârfuri, avem șanse de a obține o colorare suficient de bună — iar noi vrem chiar pe cea mai bună (în cazul de față, cu 7 culori):
G <- graph_from_adjacency_matrix(ADJ, mode="undirected") qN <- clique_num(G) # ordinul maxim al clicilor lui G (7) repeat { gvc <- greedy_vertex_coloring(G) if(max(gvc) == qN) break # returnează colorarea cea mai bună, dacă există... G <- permute(G, sample(nrv)) # permută vârfurile, păstrând adiacența }
Desigur, în formularea de mai sus repeat() va rula la nesfârșit, dacă nu există o colorare cu qN culori; nu-i cazul aici, dar dacă sesizăm această tendință, atunci după un timp, stopăm programul și îl repetăm cu if(max(gvc) == qN+1).
Pentru "Mt" avem noroc, rezultând în scurt timp următoarea 7-colorare:
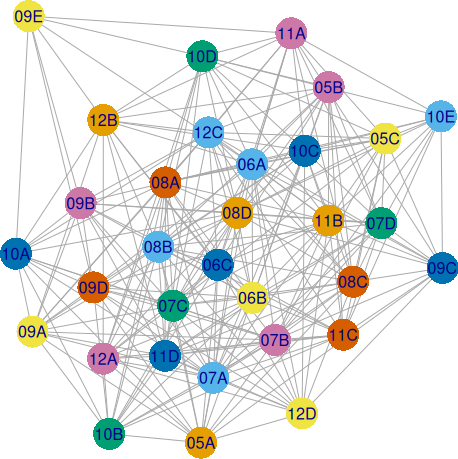
pe baza căreia, ca în cazurile anterioare, constituim lista vp și o înscriem în ORR (salvând iarăși în "orar-cl_5.RDS"):
> table(ORR$prof)
Bi1 Bi2 Bi3 Fi1 Fi2 Fi3 Fi4 Fi5 Mt1 Mt2 Mt3 Mt4 Mt5 Mt6 Mt7
759 18 19 18 18 18 18 18 3 19 21 17 19 20 18 23
Clasele alocate lui "Mt3" de exemplu, sunt cele 4 colorate green ("darkgreen"):
> ORR %>% filter(prof=="Mt3") %>% pull(cls) %>% unique() [1] 07C 07D 10B 10D # respectiv cu 5, 4, 4, 4 ore (total 17)
Bineînțeles că, luându-ne după culorile din graful redat mai sus putem reconstitui încadrările pe clase ale celor 7 profesori de "Mt" pe care i-am introdus.
(IV)... trebuie 3, nu 2, profesori de "SP"
Să ne ocupăm acum de profesorii de "Română".
Ne pregătisem de la început să includem și lecțiile de "Lit-univ" și "Latină", indicând în "Discip" vectorul celor 3 discipline; acum vedem că n-ar fi deloc bine: dacă Discip are mai mult de un singur element, atunci paste0(Discip, 1:max(gvc)) ar induce nume evident defectuoase, pentru încadrările pe clase din lista vp.
Pe de altă parte, investigând setul ORR constatăm că nu se justifică presupunerea noastră inițială, că orele de "LU" și "La" ar cădea în seama unor profesori de "Ro":
> ORR %>% filter(obj %in% c("Ro", "La"), zl=="Mi", ora==1) cls zl ora obj prof 1 05B Mi 1 Ro 2 07B Mi 1 Ro 3 07C Mi 1 La 4 07D Mi 1 Ro 5 09C Mi 1 Ro 6 09E Mi 1 Ro 7 10C Mi 1 Ro 8 11B Mi 1 Ro 9 11E Mi 1 Ro 10 12E Mi 1 Ro
Vedem că ora de "La" se desfășoară simultan cu 9 ore de "Ro"; deci există cel puțin 9 profesori de "Ro", dar niciunul dintre cei 9 implicați pe liniile redate, nu poate face și "La"… Prin urmare, cel mai firesc este ca pentru "La" și "LU" (în total, 12 ore) să inventăm un profesor diferit de cei de "Ro".
Cu Discip="Ro", repetând "enframe.R" găsim că graful G are 9 clici și ne rezultă o 9-colorare pentru care în lista încadrărilor vp avem:
Ro1 Ro2 Ro3 Ro4 Ro5 Ro6 Ro7 Ro8 Ro9
16 16 16 17 16 16 14 10 12
Conform normativelor în vigoare, de la o anumită vârstă sau vechime, profesorii pot avea "normă redusă", de la 18 la 16 ore — deci în vp avem numai 3 profesori care ar trebui să-și completeze norma într-o altă școală; altele dintre repartizările obținute, de exemplu (12 21 18 16 20 12 15 11 8) cu 5 profesori sub normă, ni se par mai proaste decât cea aleasă mai sus.
După ce înscriem în ORR încadrarea obținută vp, trecem imediat la disciplinele "LU" și "La" — pentru care procedăm astfel: propunem Discip="LL", iar pentru ZH folosim filter(obj %in% c("LU", "La")). În vp rezultă un singur profesor, cu numele "LL1", care preia cele 12 ore de "LU" și "La"; înscriindu-l și pe acesta în ORR, în "orar-cl_5.RDS" ne mai rămân 614 lecții cu "" în câmpul prof.
Pentru disciplinele Ch, Gg, Rg și SP (v. [1]) nu este cazul de lecții "pe grupe" și nici cazul de a viza eventuale discipline secundare asociate lor; pentru acestea, enframe.R ne dă imediat încadrările necesare și le înscriem pe rând în ORR. O singură dificultate apare: de exemplu pentru Rg ("Religie") rezultă doi profesori; fiindcă prin colorarea greedy prima culoare este aplicată pe cât de multe vârfuri este posibil, rezultă mereu distribuții foarte neechilibrate, precum (27, 7) — încât a trebuit să apelăm la could_move(1, 2), pentru a muta unele clase din vp[[1]] în vp[[2]].
Acum, pe ORR avem:
> table(ORR$prof) Bi1 Bi2 Bi3 Ch1 Ch2 Ch3 Fi1 Fi2 Fi3 Fi4 Fi5 Gg1 Gg2 Gg3 LL1 Mt1 Mt2 Mt3 Mt4 429 18 19 18 21 20 9 18 18 18 18 3 18 18 5 12 19 21 17 19 Mt5 Mt6 Mt7 Rg1 Rg2 Ro1 Ro2 Ro3 Ro4 Ro5 Ro6 Ro7 Ro8 Ro9 SP1 SP2 20 18 23 17 17 16 16 16 17 16 16 14 10 12 30 30
și… ne-a apărut o situație anormală: cei doi profesori înființați pentru SP ("Sport") au câte 30 de ore, ceea ce este deplasat. Trebuie să înființăm un al 3-lea profesor; pentru aceasta, întâi reconstituim vp plecând de la ORR:
vp <- map(1:2, function(i) ORR %>% filter(prof == paste0("SP",i)) %>% pull(cls) %>% unique()) %>% setNames(c("SP1","SP2"))
Apoi definim vectorul culorilor corespunzătoare celor două încadrări:
gvc <- vector("integer", vcnt) %>% setNames(CLS) gvc[vp$SP1] <- 1L gvc[vp$SP2] <- 2L
și plotăm graful G, aplicând și 2-colorarea respectivă; pe figură a fost ușor să alegem câte 5 noduri de pe cele două culori (dar încât în total să ajungem la 20 de ore) și să le asociem o a treia culoare, green (constituind astfel o 3-colorare a grafului, în loc de 2-colorarea inițială):

Apoi am introdus în vp al treilea profesor (pe clasele marcate cu green):
vp$SP3 <- c("11D", "11C", "07A", "10B", "07B", "12D", "12C", "11A", "08C", "11E")
Bineînțeles, din vp$SP1 și vp$SP2 am scos clasele alocate acum lui SP3; apoi am înregistrat în ORR noua încadrare, cu 3 profesori pe "SP", fiecare cu câte 20 de ore.
(V) Descoperirea tuplajelor
Cum ne așteptam, pentru Discip="Ds" ("Desen") și apoi cu Discip="Mz" ("Muzică") rezultă câte un profesor; aceștia au însă și lecții "MD" ("Muz/Des") pe grupe — iar pentru Discip="MD", enframe.R ne dă… doi profesori (graful G fiind 2-colorat):
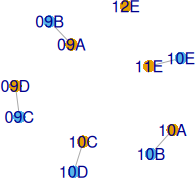
Aceasta contrazice părerea pe care ne-o formasem la început (doar privind orarele PDF originale), că ar fi vorba de cuplaje, pe grupe ale unei aceleiași clase…
12E este un nod izolat, deci în ora respectivă clasa este împărțită în două grupe, la care intră Ds1, respectiv Mz1 (fără a angaja grupe de la vreo altă clasă). În schimb, celelalte 10 clase arătate pe graful redat mai sus sunt grupate câte două; muchia 09A—09B de exemplu, are acum această semnificație: fiecare dintre cele două clase este despărțită în două grupe de elevi; în săptămâna curentă, la clasa formată din grupele_1 intră Ds1, iar la aceea formată din grupele_2 intră Mz1 (și invers, în săptămâna următoare).
În termenii introduși în [2] și [3], vorbim de tuplaje — lecții pe care doi (sau mai mulți) profesori le desfășoară într-un același timp zl|ora, la câte o clasă constituită ad-hoc din reuniunea unor grupe de la două (sau mai multe) clase (spre deosebire de cuplaj, când doi profesori lucrează în același timp zl|ora cu câte o grupă a unei singure clase).
În ORR, cele 5 tuplaje evidențiate pe graful redat mai sus și cuplajul pe clasa 12E apar toate, într-o aceeași zi (încât cei doi profesori scapă de ferestre):
> MD <- ORR %>% filter(obj=="MD") %>% as.data.frame() cls zl ora obj prof 1 09A Lu 6 MD 2 09B Lu 6 MD # tuplajul (Ds1,Mz1)/(09A,09B) 3 09C Lu 2 MD 4 09D Lu 2 MD # tuplajul (Ds1,Mz1)/(09C,09D) 5 10A Lu 3 MD 6 10B Lu 3 MD 7 10C Lu 4 MD 8 10D Lu 4 MD 9 10E Lu 5 MD 10 11E Lu 5 MD 11 12E Lu 1 MD # cuplaj pe clasa 12E
În scopul de a constitui un nou orar (… după ce vom fi terminat de înființat profesorii necesari), procedăm ca în [2]: constituim un "orar parțial" pentru cele 5 tuplaje (câte unul, aleatoriu, pe fiecare zi), atribuind prima clasă din fiecare tuplaj primului profesor și a doua celuilalt; apoi eliminăm lecțiile respective din ORR (iar la clasa 12E înscriem în câmpul prof pe obiectul "MD", cuplajul Ds1Mz1):
Zile <- levels(ORR$zl) MD <- MD %>% filter(cls != "12E") %>% select(cls, zl, prof) %>% mutate(zl = rep(sample(Zile), each = 2), prof = rep(c("Ds1", "Mz1"), time = 5)) > MD # verificare cls zl prof 1 09A Vi Ds1 2 09B Vi Mz1 # tuplajul Ds1/Mz1 pe 9A/9B (alocat zilei Vi) 3 09C Lu Ds1 4 09D Lu Mz1 # tuplajul Ds1/Mz1 pe 9C/9D (alocat zilei Lu) 5 10A Ma Ds1 6 10B Ma Mz1 7 10C Jo Ds1 8 10D Jo Mz1 9 10E Mi Ds1 10 11E Mi Mz1 saveRDS(MD, "tuplaje.RDS") MD <- ORR %>% filter(obj == "MD", cls != "12E") ORR <- anti_join(ORR, MD) # elimină din ORR, tuplajele pe Muz/Des wh <- which(ORR$cls=="12E" & ORR$obj=="MD") ORR$prof[wh] <- "Ds1Mz1" # înscrie cuplajul pe clasa 12E
Pe liniile din ORR pe care la obj avem "Ds" înscriem Ds1 în câmpul prof (și analog, pentru "Mz"); apoi, salvăm iarăși în "orar-cl_5.RDS" (desigur, pentru ca enframe.R să lucreze mereu, pe setul curent ORR).
Tuplaje buchisite sturlubatic
vezi Cărţile mele (de programare)