Orarul unei şcoli cu două schimburi, folosind R
Considerăm acum o încadrare cu două schimburi, extrasă iarăşi de pe orarul găsit pe site-ul unei anumite şcoli; este vorba de un orar bine făcut (cu ascTimetables), încât vom avea o sarcină grea… „Bine făcut” de exemplu, în privinţa numărului de ferestre: pe orarul original, în primul schimb sunt doar 11, iar la al doilea numai 20 – pe toată săptămâna; în plus, orele în ambele schimburi dintr-o aceeaşi zi sunt „legate”, pentru o bună parte a profesorilor aflaţi în această situaţie.
În [1] plecam de la încadrarea profesorilor pe clase (dintr-o şcoală cu un singur schimb) şi ignoram disciplinele de învăţământ asociate; de data aceasta plecăm chiar de la orarul original, din care deducem încadrarea (pe clase şi pe discipline) şi schimburile, iar apoi vom aplica încadrării de pe fiecare schimb programele din [1] (iar prin aplicaţiile interactive asociate acestora vom corela în final, rezultatele obţinute pe fiecare schimb).
De la PDF, la .xlsx la .RDS
Orarul original este postat pe site-ul şcolii respective, ca document PDF; încă putem folosi fără constrângeri iLovePDF, prin care transformăm documentul PDF respectiv, într-un fişier Excel "orar.profesori.xlsx" – compus în cazul de faţă dintr-un anumit număr de foi ("Table 1", "Table 2" etc.), care trebuie împerecheate consecutiv: o foaie de rang impar conţine două inscripţii, pentru numele şcolii şi respectiv numele unui profesor, iar foaia de rang următor conţine orarul profesorului respectiv, pe zilele Lu, Ma, etc. şi pe orele 1..12 ale fiecărei zile.
Următorul program reuneşte datele din foile Excel, într-un obiect R "tibble", salvat ca atare apoi, în fişierul orarOrig.RDS:
# orar_orig.R (transformă orarul original .xlsx, în "orarOrig.RDS") library(tidyverse) sheets2lst_tb <- function(xlsx="") { require(readxl) # extrage datele din tabele Excel, în obiecte R 'tibble' xlsx %>% excel_sheets() %>% set_names() %>% map(read_excel, path = xlsx) } # listă R de obiecte 'tibble' (câte unul pentru fiecare foaie Excel) ltb <- sheets2lst_tb("orar.profesori.xlsx") #$`Table 1` ## A tibble: 0 x 2 ## … with 2 variables: `Colegiul NumeColegiu` <lgl>, `Profesor NumePren` <lgl> #$`Table 2` ## A tibble: 5 x 13 # ...1 `1` `2` `3` `4` `5` `6` `7` `8` `9` `10` `11` `12` # <chr> <lgl> <lgl> <lgl> <lgl> <lgl> <chr> <chr> <chr> <chr> <chr> <chr> <lgl> #1 Lu NA NA NA NA NA NA "Rom… "Rom… "Rom… "Rom… "Rom… NA #2 Ma NA NA NA NA NA NA "Rom… "Rom… "Rom… "Rom… "Rom… NA #3 Mi NA NA NA NA NA "Rom\… "Rom… "Rom… "Rom… NA NA NA #4 Jo NA NA NA NA NA "Rom\… "Rom… "Rom… "Rom… NA NA NA #5 Vi NA NA NA NA NA "Rom\… "Rom… NA NA NA NA NA nt <- length(ltb) for(i in seq(1, nt, by=2)) { prof <- substring(names(ltb[[i]])[2], 10) # ignoră inscripţia "Profesor " nr <- nrow(ltb[[(i+1)]]) ltb[[(i+1)]]$prof <- rep(prof, nr) # "numePren" în 'Table 2', 'Table 4', etc. } LRC <- seq(2, nt, by=2) %>% map_df(., function(i) ltb[[i]]) %>% # reuneşte obiectele "tibble" relocate(., prof, before=1) %>% # coloana 'prof' devine prima coloană rename(., zl = `...1`) # redenumeşte prin 'zl', coloana zilelor #tibble [310 × 14] (S3: tbl_df/tbl/data.frame) # $ prof: chr [1:310] "NumePren" "NumePren" ... # $ zl : chr [1:310] "Lu" "Ma" "Mi" "Jo" ... # $ 1 : chr [1:310] NA NA NA NA ... # $ 2 : chr [1:310] NA NA NA NA ... # $ 3 : chr [1:310] NA NA NA NA ... # $ 4 : chr [1:310] NA NA NA NA ... # $ 5 : chr [1:310] NA NA NA NA ... # $ 6 : chr [1:310] NA NA "Rom\r\n11.D" "Rom\r\n11.D" ... # $ 7 : chr [1:310] "Rom\r\n10.C" "Rom\r\n10.C" "Rom\r\n10.G" "Rom\r\n10.D" ... # $ 8 : chr [1:310] "Rom\r\n10.D" "Rom\r\n9.C" "Rom\r\n10.G" "Rom\r\n10.C" ... # $ 9 : chr [1:310] "Rom\r\n9.C" "Rom\r\n10.D" "Rom\r\n10.B" "Rom\r\n9.C" ... # $ 10 : chr [1:310] "Rom\r\n10.G" "Rom\r\n9.C" NA NA ... # $ 11 : chr [1:310] "Rom\r\n10.B" "Rom\r\n10.B" NA NA ... # $ 12 : chr [1:310] NA NA NA NA ... saveRDS(LRC, file="orarOrig.RDS")
Normalizarea datelor; încadrări, pe schimburi şi cupluri
Celulele goale din documentul PDF original (respectiv, din tabelele Excel asociate) sunt reprezentate în R prin constanta NA (şi „celulă goală” şi NA, însemnând că profesorul este liber în ora respectivă); dacă ne gândim să prelucrăm datele respective şi nu doar să le vizualizăm pe coloane, atunci valorile NA devin inutile.
Prin următorul program, întâi „normalizăm” datele – adică eliminăm valorile inutile (majoritatea valorilor NA) şi separăm în variabile independente valorile rămase, compuse iniţial din denumirea materiei ("Rom" de exemplu) şi numele clasei ("10.B", sau "5" de exemplu), corespunzătoare orei respective a profesorului; ne îngrijim deasemenea, ca numele claselor să fie de un acelaşi format, cât mai simplu.
# orarOrig_norm.R # normalizează 'orarOrig.RDS' ==> 'orarOrigNorm.RDS' # anonimizează Prof. şi ordonează după ore/săpt. ==> 'orarNorm.RDS' # tabel de conversie 'numeProf.RDS' ("P01" ==> "Nume Prenume", etc.) # Tabelul de încadrare ==> 'incadrare.csv' # schimburi; cuplaje library(tidyverse) orar <- readRDS("orarOrig.RDS") orar <- orar %>% gather("ora", "obCls", 3:14) %>% # 'obCls': "Rom\r\n10.C" separate(obCls, c("obj", "cls"), sep="\r\n") %>% # obj="Rom", cls="10.C" filter(!is.na(cls)) %>% # ignoră valorile 'cls' goale mutate(cls = ifelse(nchar(cls) == 1, # "8" "12.D" paste0(cls, "Z"), # "8" ==> "8Z" sub(".", "", cls, fixed=TRUE))) %>% # "12.D" ==> "12D" arrange(prof) #> orar ## A tibble: 925 x 5 # prof zl ora obj cls # <chr> <chr> <chr> <chr> <chr> # 1 Alex... Ma 3 Chi 11B # 2 Alex... Vi 3 Chi 11D # 3 Alex... Ma 4 Chi 11D # 4 Alex... Vi 4 Chi 8Z ## … with 921 more rows saveRDS(orar, file="orarOrigNorm.RDS")
orarOrigNorm.RDS conţine valorile celor 5 variabile independente specifice unui orar: profesorul, obiectul, clasa (ale căror valori sunt date), ziua şi ora din zi (pentru care trebuie fixate valori potrivite); pe noi ne vor interesa numai coloanele $prof, $obj şi $cls – intenţionând să repartizăm aceste triplete de valori pe zilele de lucru şi apoi pe orele fiecărei zile, folosind programele R din [1].
Mai departe, transformăm $prof în factor ordonat (după numărul de ore pe săptămână) şi „anonimizăm” numele profesorilor, dar încă nu eliminăm coloanele $zl şi $ora (vom vedea mai încolo, de ce); salvăm obiectul tibble astfel constituit, în fişierul orarNorm.RDS. Deasemenea, salvăm în numeProf.RDS corespondenţa dintre numele introduse "P01", "P02" etc. şi numele reale ale profesorilor – pentru eventualitatea că în final am reveni la cele originale:
srt <- sort(table(orar$prof), decreasing=TRUE) orar$prof <- factor(orar$prof, levels=names(srt), ordered=TRUE) numePr <- c(paste0("P0", (1:9)), paste0("P", (10:length(srt)))) # "P01", "P02", etc. levels(orar$prof) <- numePr #tibble [925 × 5] (S3: tbl_df/tbl/data.frame) # $ prof: Ord.factor w/ 60 levels "P01"<"P02"<"P03"<..: 17 17 17 17 17 17 17 17 17 17 ... # $ zl : chr [1:925] "Ma" "Vi" "Ma" "Vi" ... # $ ora : chr [1:925] "3" "3" "4" "4" ... # $ obj : chr [1:925] "Chi" "Chi" "Chi" "Chi" ... # $ cls : chr [1:925] "11B" "11D" "11D" "8Z" ... saveRDS(orar, file="orarNorm.RDS") numeProf <- names(srt) names(numeProf) <- numePr # "P01" ==> "NumePren_original", etc. saveRDS(numeProf, file="numeProf.RDS")
Mai departe, putem obţine uşor tabelul de încadrare (câte ore are fiecare profesor, la fiecare clasă; de observat că deja nu mai avem nevoie decât de $prof şi $cls):
### Tabelul de încadrare frm <- table(orar[c('prof', 'cls')]) icls <- c("A", "B", "C", "D", "E", "F", "G") # câte 7 clase, pe 4 nivele colnames(frm) <- c(rep(icls, 3), "5", "6", "7", "8", icls) # şi 4 clase 5..8 frm[frm == 0] <- "." # cls ## 10A-G 11A-G 12A-G 5-8 9A-G # prof A B C D E F G A B C D E F G A B C D E F G 5 6 7 8 A B C D E F G # P01 2 . . 2 . . . 4 . 2 2 . . . 1 4 . . 1 . 2 . . . . . 3 . 3 . . 2 # P02 . 3 2 . . 1 1 . 5 . 2 1 . 2 4 . . 1 . . . . . . . 3 . 3 . . . . # P03 . . 2 2 . . 2 . 2 2 . . 2 . . . . . 3 2 . . 3 . . . 2 . . 2 2 2 # P04 . . . . . . 2 . . . . 1 2 . 1 1 1 1 2 3 3 . . . . 1 1 1 1 2 2 2 # P05 . . . . . . . 3 2 2 1 1 1 1 1 2 2 2 1 2 1 . . . . 1 . 1 1 . 1 . # P06 1 1 1 1 1 1 1 . . . . 1 1 1 . . 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 # P07 2 2 . . 2 2 . 2 . . 2 4 . 2 . . . . . . 2 . . 2 . 2 . . . . . . # P08 . . 4 4 . . . 4 . . 3 . . . . . 4 . . . . . . . . . . 4 . . . . # P09 1 . . . . . 2 . 1 . 1 2 1 . . 1 . 1 2 2 2 2 1 1 1 1 . . . . 1 . # P10 3 . . . 2 2 . . . . . . . . 3 . 3 . . . . . 2 2 . . . . 3 . . 2 # P11 . . . . . . . . . . . . . 2 . . . . . . 2 4 . 4 5 . 5 . . . . . # P12 . . 2 2 . 3 . . . . . 4 3 . . . . 2 . . . 2 2 2 . . . . . . . . # P13 . . . 3 . . . . 3 . 3 . . . . 3 . . . . . . . . 2 . . 3 . 2 2 . # P14 . . . . . . . . . 4 . . . 5 4 . . . . . . . . 4 4 . . . . . . . # P15 . . . . . . . . 2 . . . . 3 3 2 3 . 3 . . . . . 2 . . . . . 3 . # P16 . . . . . . . 3 . . . . . . . . . . . 5 5 . . . . 4 . . 4 . . . # P17 . 2 3 . 1 . 1 . 1 . 2 . . . . 1 . 2 . . . . . . 2 . 2 . 2 . . 1 # P18 . 3 3 3 . . 4 . . . 3 . . . . . . . . . . . . . . . . 4 . . . . # P19 . . . . 1 1 1 . . . . 3 4 . . . . . 2 . . . . 1 . . 4 . . 1 1 1 # P20 . . . . . 4 . . . . . . 1 . . 3 . 4 . . . 4 4 . . . . . . . . . # P21 3 . . . 4 . . . . . . 5 . . . . . . . . . . . . . . . . . 4 4 . # P22 2 . . 3 . 1 . 1 . 2 . . . . 1 . 2 . . . . . . 2 . 2 . 2 . 1 1 . # P23 . . . . 1 1 . . 1 . 3 2 . . . 2 . . 2 . . . 3 3 . . . . . . . 1 # P24 . . . . . . . . . . . . 2 . 4 5 . 4 . . . . . . . . . . . 2 2 . # P25 . 4 . . . . . . . 4 . . . . . . . . . . . . . . . 5 . . 4 . . 2 # P26 . 1 . . . 2 . . 1 1 . . . . . . . 1 . 2 2 1 . 2 2 1 . . 1 . 2 . # P27 . 3 3 . . . . 3 . 3 . . . . . . . 3 . . . . . . . 3 . . . . . . # P28 . 1 . . . . . . . 1 . 2 . . . . . . 4 5 . . . . . 1 . 1 . . . 3 # P29 2 . 2 2 . . 1 2 . . . . . . 1 . . 3 . . . . . . . . 2 . 3 . . . # P30 . . . . 3 3 . 1 . . 1 . . 4 . . . . . . . 2 . . . . . . 1 . 3 . # P31 2 . 2 2 1 1 1 . . . . . . . . . . . . . . 2 2 2 2 . . . . . . 1 # P32 2 . . . 3 . . 2 . 2 . . . . . . . . . 2 . . . . . . 2 2 . 3 . . # P33 . . . . . . . . . . . . . . 2 2 2 2 . . . 2 . . 3 . . 2 2 . . . # P34 . 2 . . . . 3 . . . 2 . . . . . . . . . 2 . . . . 2 . . 2 . . 3 # P35 1 . . . . . 3 . 1 . . . 3 . . . 1 1 . . 5 . . . . . 1 . . . . . # P36 . . . . . . . . 3 . . . . . . . 4 . 5 . . . . . . . . . . . . 4 # P37 . 1 1 1 1 1 . 1 . 1 . . 1 1 1 . 1 . . . . . . . . . 1 1 1 1 . 1 # P38 . 2 . . . . . . . 3 . . . . . . 2 . . . . 2 . . 1 2 . 3 . . 1 . # P39 5 . . . . . 2 . 5 . . . . . . . . . . . . . 4 . . . . . . . . . # P40 1 1 1 1 1 1 1 . . . . 1 2 2 . . . . . . . . . . 1 . . . . . . . # P41 . . . . 3 3 . . . . . . . 2 . . . . . . . 1 1 1 . . . . . . . . # P42 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 1 1 1 # P43 . . . . 1 . . . . . . . 2 . . . . . 1 1 . . . . . . . . . 2 2 . # P44 1 . . . . . 2 1 . . . . 2 2 . . . . . . . . 1 . . . . . . . . . # P45 . . . . . . . . . . 1 . . . 1 1 1 . 1 . . . . . . . . . . 2 . . # P46 . . . . . . . . . . . . . . 1 . . . . . . . . 1 2 . . . . 3 . . # P47 . . 1 1 2 . . . . . . 1 . . . . . . . . . . . . . . . . . . . 2 # P48 . . . . 1 1 1 . . . . . . . . . . . . . . 1 1 1 1 . . . . . . . # P49 . . . . 2 2 . . . . . . . . . . . . . 2 . . . . . . . . . . . . # P50 . . . . . . 2 . . . . . . . . . . . . . . . . . . . 3 . . . . . # P51 . . 1 1 . . . . . . . . . 1 . . . . . 1 1 . . . . . . . . . . . # P52 . . . . . . . . . . . . . . . . 1 . . . . 1 1 1 1 . . . . . . . # P53 . 2 . . . . . . . . . . . . . . . . . . . . . . . . 1 . . 1 . . # P54 1 1 . . . . . . . . 1 . 1 . . . . . . . . . . . . . . . . . . . # P55 . . . . . . . . . . . . . . . . . . . . . 1 1 1 1 . . . . . . . # P56 . . . . . . . 1 1 1 1 . . . . . . . . . . . . . . . . . . . . . # P57 . . 1 1 . . . . . . . . . . . . . . . . . . 1 . . . . . . . . . # P58 . . . . . . . . . . . . . . . . . . . . . . . . . . 1 1 . . . . # P59 . . . . . . . . . . . . . . . 1 . . . . . . . . . . . . . . . . # P60 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1 . .
Dar vom avea de lucrat pe fiecare schimb în parte; unele clase au zile cu 5 ore şi încep ziua de la a doua oră:
# SCHIMBURI schimb <- function(h) with(orar, sort(unique(cls[ora==h]))) Sch1 <- schimb(2) # clasele din primul schimb (au ora `2`, totdeauna) Sch2 <- schimb(11) # clasele din al doilea schimb (au ora `11`, totdeauna) or1 <- orar %>% filter(cls %in% Sch1) or2 <- orar %>% filter(cls %in% Sch2) saveRDS(or1, file="orarNormS1.RDS") saveRDS(or2, file="orarNormS2.RDS")
Să reţinem şi tabelele de încadrare, ca fişiere CSV (din care, prin read_csv() putem obţine un obiect 'tibble' corespunzător, oricând am avea nevoie ulterior în vreun program):
wr_incdrCSV <- function(orar, ...) { # extrage încadrarea, într-un fişier CSV frm <- table(orar[c('prof', 'cls')]) frm[frm == 0] <- "" dfi <- frm %>% as.data.frame.matrix(.) %>% mutate(prof = row.names(frm)) %>% relocate(., prof, before=1) write_csv(dfi, ...) } wr_incdrCSV(orar, file="incadrare.csv") wr_incdrCSV(or1, file="incadrareS1.csv") wr_incdrCSV(or2, file="incadrareS2.csv")
În sfârşit, avem de observat că în coloana $zl apar şi valori NA, pentru care deducem această semnificaţie: profesorul care are NA în coloana $zl este cuplat la o aceeaşi clasă şi într-o aceeaşi oră cu un alt profesor – care, dacă ordonăm după clase, apare pe linia precedentă:
## CUPLURI (în schimbul al doilea) or2 %>% filter(prof %in% c("P42", "P06", "P48")) %>% arrange(cls) %>% print(n=Inf) # A tibble: 32 x 5 # prof zl ora obj cls # 1 P06 Vi 11 Ed.Viz 10A # 2 P42 NA 11 Ed.Muz 10A # "P42" şi "P06" sunt cuplaţi la clasa 10A # 3 P06 Vi 12 Ed.Viz 10B # 4 P42 NA 12 Ed.Muz 10B # 5 P06 Vi 8 Ed.Viz 10C # 6 P42 NA 8 Ed.Muz 10C # 7 P06 Mi 12 Ed.Viz 10D # 8 P42 NA 12 Ed.Muz 10D # 9 P06 Lu 7 Ed.Viz 10E #10 P48 NA 7 Ed.Muz 10E #11 P06 Lu 8 Ed.Viz 10F #12 P48 NA 8 Ed.Muz 10F #13 P06 Lu 9 Ed.Viz 10G #14 P48 NA 9 Ed.Muz 10G #15 P06 Lu 11 Ed.Viz 5Z # "P06" intră singur la clasa "5Z" #16 P48 Lu 12 Ed.Muz 5Z # "P48" intră singur la clasa "5Z" #17 P06 Ma 11 Ed.Viz 6Z #18 P48 Lu 11 Ed.Muz 6Z #19 P06 Mi 10 Ed.Viz 9A #20 P42 NA 10 Ed.Muz 9A #21 P06 Mi 11 Ed.Viz 9B #22 P42 NA 11 Ed.Muz 9B #23 P06 Vi 7 Ed.Viz 9C #24 P42 NA 7 Ed.Muz 9C #25 P06 Vi 10 Ed.Viz 9D #26 P42 NA 10 Ed.Muz 9D #27 P06 Lu 10 Ed.Viz 9E #28 P42 Jo 10 Ed.Muz 9E #29 P06 Lu 12 Ed.Viz 9F #30 P42 Jo 12 Ed.Muz 9F #31 P06 Ma 12 Ed.Viz 9G #32 P42 Jo 11 Ed.Muz 9G
Cuplajele apar numai în schimbul al doilea; notăm (pentru cazul când vom anexa interactiv orele cuplate) că "P06" este cuplat cu "P42" la clasele 9A-D şi 10A-D şi este cuplat cu "P48" la clasele 10E-G; în total, avem 11 ore cuplate, iar fiecare dintre cei trei profesori angajaţi în câte un cuplu, are şi ore proprii.
Dar avem o situaţie „fericită”: orele proprii sunt la alte clase, decât cele pe care sunt cuplaţi (era mai complicat de gestionat situaţia când un profesor are la o aceeaşi clasă şi ore proprii şi ore cuplate); prin urmare, ar trebui să fie suficient să reţinem numai cele 11 linii cu NA în coloana $zl, într-un obiect 'tibble' separat (sperând să-l putem folosi cumva, în programele de distribuire pe zile şi pe orele zilei; să ne amintim că în [1] cuplajele erau ignorate în aceste programe, fiind tratate interactiv după generarea distribuţiilor):
cupl <- or2 %>% filter(is.na(zl)) %>% select(prof, obj, cls) saveRDS(cupl, file="cuplaje2.RDS") # prof obj cls # 1 P48 Ed.Muz 10E # 2 P48 Ed.Muz 10F # 3 P48 Ed.Muz 10G # 4 P42 Ed.Muz 9C # 5 P42 Ed.Muz 10C # 6 P42 Ed.Muz 9A # 7 P42 Ed.Muz 9D # 8 P42 Ed.Muz 9B # 9 P42 Ed.Muz 10A #10 P42 Ed.Muz 10D #11 P42 Ed.Muz 10B
Cu aceasta încheiem programul orar_origNorm.R; avem acum încadrarea profesorilor pe fiecare schimb (şi în format CSV, dar şi ca obiecte 'tibble', în fişiere .RDS), iar mai departe vom ignora valorile iniţiale (originale) din coloanele $zl şi $ora.
Pregătiri
Creem un subdirector STMT/ (amintind eventual termenul "school timetable problem") în care mai întâi, plasăm încadrările prof|obj|cls corespunzătoare celor două schimburi (şi în plus, copiem sau chiar mutăm aici, fişierul cuplaje2.RDS):
or1 <- readRDS("orarNormS1.RDS") %>% select(prof, obj, cls) %>% saveRDS(., file="STMT/frame1.RDS") # analog pentru STMT/frame2.RDS
frame1.RDS şi frame2.RDS provin în fond, prin filtrare, din orarNorm.RDS – deci se păstrează calitatea coloanei $prof de a fi "factor ordonat", având ca nivele numele tuturor profesorilor (chiar şi ale acelora care nu au ore în unul dintre schimburi – ceea ce este foarte bine, uşurându-ne corelarea schimburilor), în ordinea dată de numărul total de ore pe săptămână – ceea ce nu mai este bine, fiind incluse orele din ambele schimburi; va trebui să reordonăm cumva, după numărul de ore pe fiecare schimb în parte.
Apoi, copiem în STMT/ programele din [1], distribute_by_days.R şi set_hours_day.R (dar şi fişierul lstPerm47.RDS); va trebui să facem anumite modificări (deja am observat unele mai sus) în aceste programe, fiindcă acum operăm pe schimburi.
Apoi, copiem în STMT/ subdirectorul recast/, care conţine fişierele HTML, JS şi CSS ale aplicaţiilor interactive pe care le vom folosi ca şi în [1], pentru finalizarea distribuţiilor generate prin programele menţionate (probabil că şi pe aceste fişiere, vom avea de făcut anumite modificări – de aceea ni le punem la dispoziţie imediată).
Repartizarea pe zilele de lucru a încadrărilor
Programul distribute_by_days.R din [1] repartizează pe zilele de lucru orele dintr-o încadrare a profesorilor pe clase, asigurând distribuţii individuale "cvasi-omogene" pentru profesorii care au un număr suficient de mare de ore; l-am mai redat anterior (îmbunătăţind mereu câte ceva), dar se pare că trebuie să-l rescriem de fiecare dată – fiindcă prevede o parte „introductivă” în care trebuie stabilite anumite variabile „globale”, depinzând de încadrarea pentru care vrem distribuţia pe zile (dar n-ar fi decât un artificiu, separarea acestei părţi într-un alt program, de rulat înainte de a aplica funcţia principală alloc_by_class()).
Rescriem deci programul (îl redăm iarăşi complet, fiindcă între timp am făcut unele mici corecturi)… Pentru fiecare schimb avem la început câte un anumit număr de linii (v. programul, mai jos); pentru distribuţia pe zile a unui schimb, trebuie decomentate liniile asociate lui şi comentate liniile asociate celuilalt. Deşi 'FRM' are un număr mic de linii (fiecare schimb are nu mai mult de 500 de ore), am exclus coloana $obj, care chiar nu joacă nici un rol în cursul repartizării pe zile (ba chiar ne-ar putea încurca, prin faptul că un profesor ar putea face mai multe obiecte la unele clase).
N-am găsit o modalitate convenabilă de integrare în alloc_by_class() a cazului orelor cuplate; dar în loc să le eliminăm de la cei 3 profesori cuplaţi, urmând să le anexăm interactiv în final (cum am procedat în [1]) – dispunem de o tratare mai simplă, decurgând din faptul că "P42" şi "P48" sunt cuplaţi fiecare cu "P06" şi fiecare dintre aceştia trei nu are ore proprii la clasele pe care sunt cuplaţi: le eliminăm (prin anti_join()) numai de la "P06" (v. mai jos, liniile pentru "Schimbul 2"), urmând ca în final să lăsăm 2 zile fără ore lui "P06", iar în aceste 2 zile să plasăm acele ore ale lui "P42" şi "P48" care trebuie făcute împreună cu "P06".
În programul redat în [1] defineam direct în alloc_by_class() matricea prin care se controlează numărul de ore pe zi alocate curent profesorilor, greşind totuşi denumirea coloanelor acesteia prin levels(FRM$prof): în momentul respectiv, FRM$prof este NULL fiindcă FRM este deja o listă de „tabele” (având drept chei, valorile $cls). Acum am corectat, folosind levels(FRM$prof) înainte de a împărţi FRM după clase; este firesc atunci, să mutăm definiţia matricei de control în „zona globală” (şi se pare că astfel, creşte uşor şi viteza de execuţie – contextul de execuţie curent al funcţiei fiind eliberat de matricea respectivă).
Căror profesori, încercăm să le asigurăm distribuţii omogene, sau măcar cvasi-omogene? În orice caz, nu acelora care au puţine ore; aceştia vor prefera de regulă să le facă în cât mai puţine zile (deci le căutăm distribuţii ne-omogene) – ceea ce este posibil cu o condiţie: orele respective să fie la clase diferite (nu prea se cade să pui două ore de obiect într-o aceeaşi zi, la o clasă!).
În [1], vizând un singur schimb (cu vreo 1200 ore), asiguram distribuţii cvasi-omogene (numărul de ore pe zi variază cu cel mult 2), pentru cei cu măcar 10 ore pe săptămână; acum, având câte un schimb cu puţine ore (sub 500 ore), vizăm distribuţii chiar omogene (numărul de ore pe zi variază cu cel mult 1), celor cu măcar 12 ore, să zicem (dar este drept că de data aceasta, n-ar trebui să ne intereseze prea mult „omogenitatea” distribuţiilor individuale – având în vedere că vrem să reducem cazurile când profesorul are ore şi într-un schimb şi în celălalt într-o aceeaşi zi).
# distribute_by_days.R repartizează pe zile (omogen), încadrarea profesorilor library(tidyverse) # Pentru schimbul 1: # FRM <- readRDS("frame1.RDS") %>% select(prof, cls) # ignorăm 'obj' # many_hours <- 11 # profesorii cu "multe" ore vor avea distribuţii omogene # Pentru schimbul 2: FRM <- readRDS("frame2.RDS") %>% select(prof, cls) # fără 'obj' cupl <- readRDS("cuplaje2.RDS") %>% select(prof, cls) %>% # fără 'obj' mutate(prof = "P06") FRM <- anti_join(FRM, cupl) # elimină lui "P06", orele cuplate cu "P42" sau "P48" many_hours <- 11 # profesorii cu "multe" ore vor avea distribuţii omogene nrPr <- nlevels(FRM$prof) # NU depinde de schimbul curent levZ <- levels(FRM$prof) # (_înainte de a transforma 'FRM' în listă pe clase!) srt <- sort(table(FRM$prof), decreasing=TRUE) FRM <- FRM %>% arrange(match(prof, names(srt))) %>% # în ordinea numărului de ore pe schimb split(.$cls) # _listă de "tabele", câte unul de clasă # Prin lista 'prOf' şi matricea 'ZH' controlăm numărul de ore/zi cumulat, la profesori prmh <- names(srt[srt > many_hours]) # _numele profesorilor cu "multe" ore cls_mh <- map(FRM, function(K) { lpr <- unique(K$prof); lpr[lpr %in% prmh] }) # listă 'cls' ==> profesorii cu "multe" ore la acea clasă ZH <- matrix(data=rep(0L, 5*nrPr), nrow = 5, ncol = nrPr, byrow=TRUE, dimnames = list(1:5, levZ)) # alocă orele pe zile, pentru fiecare clasă din 'FRM' (corelând după profesori) alloc_by_class <- function() { Zore <- ZH # iniţializează matricea de control a numărului de ore alocate # Condiţii impuse unei distribuţii a orelor (omogenitate) CND <- function(More, lpr) { mex <- Zore[, lpr] + More[, lpr] # la profesorii cu peste 'many_hours' for(j in 1:ncol(mex)) { Pr <- mex[, j] # câte ore ar avea, în fiecare zi, profesorul for(oz in Pr) if(any(abs(Pr - oz) > 1)) # > 2 (pentru "cvasi-omogenă") return(FALSE) # refuză alocarea, dacă nu este "omogenă" } return(TRUE) # acceptă alocarea: este "omogenă" (sau "cvasi-") } # montează coloana zilelor alocate orelor unei clase labelsToClass <- function(Q) { # 'Q' conţine liniile din FRM cu aceeaşi 'cls' lpr <- cls_mh[[Q$cls[1]]] # cat(paste(Q$cls[1], Q$prof[1]), "; ") # etichetează liniile din 'Q' cu 1..5 (distribuie pe zile, orele clasei) S <- Q %>% mutate(zl = rep_len(1:5, nrow(.))) # verifică dacă orele pe zi alocate profesorilor clasei respectă CND() more <- t(as.matrix(table(S[c('prof', 'zl')]))) if(CND(more, lpr)) { Zore <<- Zore + more # actualizează numărul de ore pe zi return(S) # o distribuţie care îndeplineşte condiţiile } # dacă nu-s îndeplinite CND(), _permută profesorii clasei şi reia R <- Q %>% arrange(match(prof, sample(unique(prof))), prof) return(labelsToClass(R)) # Reia dacă nu-s îndeplinite condiţiile } # (programul va fi stopat dacă reapelarea nu mai este posibilă) tryCatch( # previne pe cât se poate, stoparea programului (v. [1] etc.) { FRM %>% # etichetează liniile fiecăreia dintre clase map_df(., function(K) labelsToClass(K)) }, error = function(err) { # s-a depăşit capacitatea stivei de apeluri FRM <- FRM %>% sample(.) # permută _grupurile de linii ale claselor tryCatch({ cat("1") ## vizualizează cumva, reluările alloc_by_class() # reia de la capăt, în noua ordine de clase }, error = function(e) NULL ) } ) # Returnează distribuţia pe zile a orelor (sau eventual, NULL) }
După ce comentăm/decomentăm secvenţele de la început asociate celor două schimburi, putem obţine – dar nu prea repede, fiindcă am pretins „omogen” în loc de „cvasi-omogen” – distribuţiile byDays1.rds şi respectiv, byDays2.rds printr-o secvenţă de program precum:
source("distribute_by_days.R") Dis <- alloc_by_class() Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") Dis <- Dis %>% mutate(zl = factor(zl, labels = Zile)) saveRDS(Dis, file = "byDays1.rds") # distribuţie pe zile, primul schimb
Parcurgând aleatoriu clasele şi profesorii (pentru a eticheta convenabil cu zile, orele respective), execuţia se poate încheia în cel mai fericit caz în 1-2 minute, dar poate dura şi 10-15 minute sau mai mult; relansând programul, se obţine o nouă distribuţie (sau poate doar NULL), într-un timp poate mai scurt, poate mai lung.
Pregătirea finalizării interactive a distribuţiei pe zile
Nu vom folosi aplicaţia /recast pentru fiecare schimb în parte – ci „deodată”, pentru ambele schimburi!
Prin următorul program constituim fişierul Dis12.csv, în formatul cerut de /recast, conţinând câte două rânduri pentru fiecare profesor, astfel încât rândurile de rang impar să conţină clasele repartizate pe zile în primul schimb, iar cele de rang par să conţină clasele repartizate pe zile în al doilea schimb.
# dis2recast.R (reuneşte distribuţiile schimburilor, producând CSV) library(tidyverse) D1 <- readRDS("byDays1.rds") %>% mutate(sch = 1) D2 <- readRDS("byDays2.rds") %>% mutate(sch = 2) lDz <- rbind(D1, D2) %>% arrange(prof, sch) %>% split(.$zl) # modelează tabelul necesar aplicaţiei /Recast (scriindu-l apoi în format CSV) Drc <- data.frame(prof="", Lu="", Ma="", Mi="", Jo="", Vi="") row = 1 for(P in levels(D1$prof)) { for(s12 in 1:2) { Drc[row, 1] <- P for(q in 2:6) { ql <- lDz[[q-1]] %>% filter(prof == P & sch == s12) Drc[row, q] <- paste(c(ql$cls), collapse=" ") } row <- row + 1 } } write_csv(Drc, file="Dis12.csv")
Copiem Dis12.csv în elementul <textarea> din recast/recast.html, apoi încărcăm recast.html în browser (Firefox); folosind butoanele aplicaţiei lansate astfel (v. [1]), vom modifica distribuţia pe zile existentă, urmărind cam cinci aspecte:
— pentru fiecare profesor, numărul de ore pe zi să nu depăşească 6; în plus, exceptând profesorii cu puţine ore, numărul total de ore să fie distribuit cât mai echilibrat pe zile;
— numărul situaţiilor în care un profesor vine în ambele schimburi într-o aceeaşi zi, să fie cât mai mic;
— profesorii care au puţine ore, să şi le facă în cât mai puţine zile;
— orele cuplate să fie aşezate „corect” pe zile, profesorilor implicaţi;
— numărul total de ore să fie distribuit cât mai echilibrat pe zile.
Ilustrăm (în principiu) genul de operaţii pe care le intenţionăm, pe acest caz:

"P03" are în ziua Jo 7 ore (3 în primul schimb, 4 în al doilea); observăm că niciuna dintre clasele de Jo nu se regăsesc în ziua Lu; mutând pe prima linie (corespunzătoare schimbului 1) cele 3 clase din ziua Jo în ziua Lu şi apoi pe a doua linie, cele două clase din ziua Lu în ziua Jo – rezultă o distribuţie în care "P03" are Lu 5 ore, numai în primul schimb şi are Jo 6 ore, numai în al doilea schimb. Să observăm că putem elibera încă o jumătate de zi: mutăm 11B din ziua Ma, în ziua Mi (dar nu în ziua Lu, unde există deja un 11B) şi totodată, 9G din ziua Mi în ziua Ma (încât în ziua Mi să nu fie 7 ore).
Desigur, mutarea unei clase dintr-o zi în alta (prin operaţia SWAP) atrage modificarea numărului total de ore pe zilele respective (şi de cele mai multe ori, trebuie făcută şi o mutare inversă a clasei respective, la un alt profesor); va trebui să urmărim numărul total de ore pe zi şi pe fiecare schimb în parte – aşa că am modificat puţin recast.js, încât să vedem totalul curent de ore pe zi pentru fiecare schimb.
Redăm parţial situaţia iniţială (pentru o distribuţie obţinută ulterior celeia de pe care am ilustrat mai sus pentru "P03"), imediat după lansarea aplicaţiei /recast:
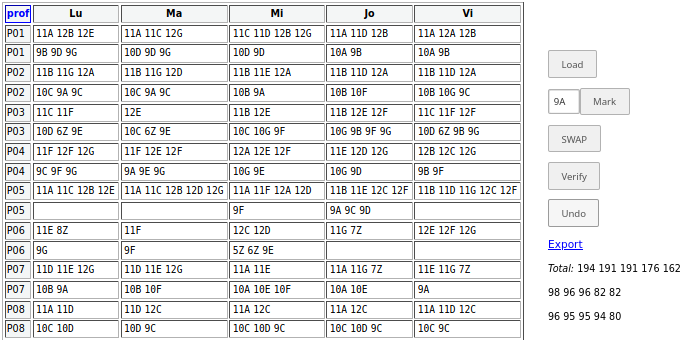
Totalul orelor pe zi descreşte de la prima spre ultima zi, fiindcă alloc_by_class() etichetează orele cu zile, pentru fiecare clasă, în ordinea obişnuită a zilelor (deci Lu vor fi totdeauna cel mai multe şi Vi cel mai puţine); încă nu avem o idee simplă pentru a corecta direct (în program şi nu interactiv), această deficienţă.
Revizuim şi handler-ul de click pentru Mark (din recast.js), fiindcă vrem să fie marcate nu numai liniile corespunzătoare clasei indicate, dar şi liniile împerecheate acestora în celălalt schimb:
bar.find('button:contains(Mark)').on('click', function(event) { let clasa = $(this).prev().val(); got.find('tr:gt(0)').toggle(); // 'got' referă tabelul HTML if(!clasa) { got.find('div').removeClass('highl'); got.find('tr:gt(0)').show(); } else { let Q = got.find('div:contains(' + clasa +')').toggleClass('highl') .parent().parent(); // marchează clasa pe liniile care o conţin Q.show(); if(Self.spreadz["Sch1"]) { if(/[0|9|5|6]/.test(clasa)) // clasă din schimbul 2 Q.prev().show(); else Q.next().show(); } $(this).prev().val(''); } });
Self.spreadz este un „dicţionar” (intern instanţei curente "Self" a widget-ului) care asociază fiecărei clase câte un tablou conţinând numărul de ore pe fiecare zi, pentru acea clasă; iniţial, în acest dicţionar aveam şi cheia "Total", asociată cu tabloul conţinând numărul total de ore pe fiecare zi; acum, am adăugat câte o nouă cheie ("Sch1" şi "Sch2"), pentru numărul total de ore pe zi corespunzător fiecărui schimb (pentru cazul când fişierul CSV pastat în <textarea> reprezintă două schimburi, adică primele două rânduri corespund unui aceluiaşi profesor).
Când clasa indicată lui Mark este una din schimbul doi, se afişează şi liniile care le preced pe cele care conţin clasa respectivă (selectate prin .prev()); analog, pentru o clasă aflată în primul schimb.
Redistribuirea în paralel, a orelor celor două schimburi
Ne ocupăm întâi de cuplaje. Putem vedea situaţia celor 3 profesori cuplaţi, într-o sesiune interactivă de lucru cu R:
vb@Home:~/21apr/LRC/STMT$ R -q > library(tidyverse) > dis <- read_csv("Dis12.csv") > dis %>% filter(prof %in% c("P06", "P42", "P48")) %>% arrange(prof) # A tibble: 6 x 6 prof Lu Ma Mi Jo Vi 1 P06 11E 8Z 11F 12C 12D 11G 7Z 12E 12F 12G 2 P06 9G 9F 5Z 6Z 9E NA NA 3 P42 NA NA NA NA NA 4 P42 10C 10D 9A 9F 10A 9D 9G 9E 9B 10B 9C 5 P48 NA 7Z 8Z NA NA NA 6 P48 NA 10G 10F 6Z 10E 5Z NA
"P06" trebuie cuplat cu "P42" pe clasele 10A-D şi 9A-D şi vedem că 5 dintre acestea figurează deja în zilele Lu şi Ma, pe linia 4; trecând în panoul în care am deschis aplicaţia /recast, constatăm folosind operaţia Mark că 9G şi 9F (care figurează la "P06" în zilele Lu şi Ma) au în ziua Vi numai câte 5 ore (iar în celelalte zile, câte 6 ore). Folosind SWAP, mutăm clasele 9G şi 9F ale lui "P06", în ziua Vi; ar mai trebui să mutăm la "P42" clasa 9G din ziua Ma în ziua Mi (la fel, pentru 9F din ziua Lu) şi clasele 10B 9C din ziua Vi fie în ziua Lu, fie în ziua Ma – şi atunci, cuplul "P06+P42" va putea să-şi facă orele în zilele Lu şi Ma.
Desigur, mutările specificate mai sus prin „ar mai trebui” necesită fiecare şi câte o mutare inversă, pentru a păstra numărul de ore pe zi la clasa respectivă; nu-i cazul să redăm aici toate mutările – după ce le-am efectuat, am folosit Export, obţinând fişierul rDis12.csv şi relansând secvenţa de comenzi R redată mai sus – înlocuind "Dis12.csv" cu "rDis12.csv" – avem următoarea redistribuire:
prof Lu Ma Mi Jo Vi
1 P06 11E 8Z 11F 12C 12D 11G 7Z 12E 12F 12G
2 P06 NA NA 5Z 6Z 9E NA 9G 9F
3 P42 NA NA NA NA NA
4 P42 10C 10D 9A 9B 10A 9D 10B 9C 9E 9G 9F NA NA
5 P48 NA 7Z 8Z NA NA NA
6 P48 NA NA 6Z 5Z 10E 10G 10F NA
Acum "P06" nu mai are ore proprii în schimbul 2 de Lu, Ma şi Jo, încât poate face orele pe care este cuplat cu "P42" şi respectiv cu "P48". Să observăm că "P06" are multe ore în primul schimb şi mai are 5 ore proprii în al doilea schimb – încât tot ce mai putem face este să-i eliberăm schimbul 1 pe o singură zi, de exemplu mutând 11F din ziua Ma, în ziua Vi.
Prin mutările efectuate deja, totalul de ore pe zi a scăzut puţin pe Lu şi Ma, crescând corespunzător pe Jo şi Vi. Mai departe, vizând prin Mark fiecare clasă în parte, continuăm să mutăm clase din primele zile spre ultimele, încât să echilibrăm totalurile de ore pe zi (eventual şi pentru fiecare schimb în parte); desigur, căutăm să alegem acele mutări de clase care să asigure şi alte obiective (eliberarea unui schimb la un profesor sau altul, comasarea într-o aceeaşi zi sau în cât mai puţine zile, a orelor celor care au un număr mic de ore pe săptămână, etc.).
Ia ceva timp (peste o oră de lucru), până epuizăm posibilităţile mai evidente, de îmbunătăţire a distribuţiei (bineînţeles că vom putea relua, dacă va fi cazul); salvăm prin Export, obţinând un nou fişier rDis12.csv. Precizăm că în final, pe fiecare zi ne-a rezultat cam acelaşi număr de ore (distribuţia pe schimburi este acum (91 91 91 90 91) şi repectiv, (92 92 92 92 92)).
Pregătirea generării orarelor zilnice
Programul set_hours_day.R din [1] vizează un singur schimb şi alocă orele 1..7 lecţiilor repartizate într-o aceeaşi zi. Amintim că în rDis12.csv (ignorând linia de antet CSV), liniile de rang impar ţin de schimbul 1, iar cele de rang par ţin de schimbul 2; deci mai întâi, trebuie să separăm rDis12.csv în fişierele rDis1.csv (conţinând liniile corespunzătoare schimbului 1) şi rDis2.csv (pentru schimbul 2):
vb@Home:~/21apr/LRC/STMT$ awk 'NR % 2 == 1' rDis12.csv > rDis1.csv vb@Home:~/21apr/LRC/STMT$ awk 'NR % 2 == 0' rDis12.csv > rDis2.csv
Precizăm pentru orice eventualitate, că în awk, variabila internă NR păstrează indexul liniei curente (deci 'NR % 2 == 1' selectează liniile de rang impar).
Avem grijă desigur, să inserăm şi linia de antet, în fişierele CSV obţinute…
Alocarea profesorilor pe orele 1..7 ale zilei decurge pentru fiecare clasă în parte, în cadrul funcţiei mountHtoDay() – pasându-i ca argument un obiect 'tibble' conţinând liniile (cu structura prof|cls) corespunzătoare clasei (pentru ziua respectivă); pentru a obţine aceste obiecte, trebuie întâi să transformăm rDis1.csv şi rDis2.cvs în obiecte 'tibble' (cu structura prof|cls|zl), pe care apoi să le divizăm după zile:
# csv2df.R (normalizează distribuţia pe zile primită în format CSV) library(tidyverse) Dcsv <- read_csv("rDis1.csv") # distribuţia pe zile Schimb-1, format CSV # Dcsv <- read_csv("rDis2.csv") # distribuţia pe zile Schimb-2, format CSV splt <- function(Txt) unlist(strsplit(Txt, " ")) renormalize <- function(D) { # v. [1] D %>% gather("zl", "cls", 2:6, na.rm=TRUE) %>% mutate(ncl = unlist(lapply(.$cls, function(q) length(splt(q))))) %>% uncount(.$ncl) %>% split(., .$cls) %>% map_df(., function(G) { q <- splt(G$cls[1]) G$cls <- rep(q, nrow(G) %/% length(q)) as.data.frame(G) }) } Din <- renormalize(Dcsv) %>% select(-4) # elimină coloana $ncl Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") srt <- sort(table(Din$prof), decreasing=TRUE) Dzl <- as_tibble(Din) %>% mutate(prof = factor(prof, levels=names(srt), ordered=TRUE), zl = factor(zl, levels=Zile, ordered=TRUE)) %>% relocate(cls, .after=prof) %>% arrange(prof) # prof (ord.) | cls | zl (ord.) saveRDS(Dzl, "rDis1z.RDS") # distribuţia pe zile Schimb-1, normalizată # saveRDS(Dzl, "rDis2z.RDS") # distribuţia pe zile Schimb-2, normalizată
Rulând csv2df.R de două ori (comentând/decomentând liniile pentru "Schimb-1" şi "Schimb-2"), obţinem obiectele 'tibble' rDis1z.RDS şi rDis2z.RDS conţinând distribuţiile pe zile pentru schimbul 1 şi respectiv, schimbul 2, în format „normal” prof|cls|zl.
Avem apoi de separat pe fiecare zi în parte, distribuţiile pe zile ale schimburilor:
# dis_of_day.R (separă din distribuţia pe zile, distribuţia pe fiecare zi în parte) library(tidyverse) Dzl <- readRDS("rDis1z.RDS") # distribuţia pe zile, prof|cls|zl (Schimb 1) # Dzl <- readRDS("rDis2z.RDS") # distribuţia pe zile, prof|cls|zl (Schimb 2) Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") # orele repartizate zilei, ordonate după profesori şi separate după clasă disOfDay <- function(zi) { Dzl %>% filter(zl == zi) %>% select(prof, cls) %>% arrange(prof) %>% # arrange(desc(prof)) split(.$cls) %>% saveRDS(., file = paste0("Dis1_", zi, ".RDS")) # Schimb 1 # saveRDS(., file = paste0("Dis2_", zi, ".RDS")) # Schimb2 } lapply(Zile, disOfDay) Bits <- rep(0L, nlevels(Dzl$prof)) # pentru a urmări alocările de ore la profesori names(Bits) <- levels(Dzl$prof) saveRDS(Bits, file="Bits1.RDS") # Schimb 1 # saveRDS(Bits, file="Bits2.RDS") # pentru Schimb 2
Rulând dis_of_day.R pentru fiecare schimb, obţinem acele obiecte 'tibble' despărţite pe clase, care vor trebui pasate pe rând funcţiei mountHtoDay() – cinci pentru primul schimb (Dis1_Lu.RDS, etc.) şi cinci pentru al doilea (Dis2_Lu.RDS, etc.).
În plus, am formulat şi tablourile de valori „cu nume”, Bits1.RDS şi Bits2.RDS care urmează să fie folosite în mountHtoDay() pentru a urmări ca alocările orare ale profesorilor clasei curente să nu se suprapună celor anterior făcute acestora la alte clase (v. [1] şi cele emergente din [1]).
Este important de sesizat că nu putem folosi un acelaşi tablou Bits.RDS pentru ambele schimburi (decât dacă am fi observat mai din timp despre ce este vorba…), fiindcă în csv2df.R mai sus, am definit $prof ca 'factor' pentru fiecare dintre obiectele 'tibble' asociate schimburilor – încât nivelele lui $prof (ca şi ordinea acestora) pentru un schimb nu sunt aceleaşi cu cele pentru celălalt schimb! (unii profesori au ore numai într-unul dintre schimburi).
Generarea orarelor zilnice
Redăm complet şi programul de generare a orarelor zilnice din [1], având acum unele mici modificări (faţă de tabloul 'Bits' al octeţilor de alocare pe orele zilei):
# set_hours_day.R (setează orele 1..7 lecţiilor repartizate într-o aceeaşi zi) library(tidyverse) Pore <- readRDS("lstPerm47.RDS") # lista matricelor de permutări (de 4..7 ore) Bits <- NULL # "placeholder" pentru alocare 1..7 fiecărui profesor (v. HELPER) ## alocă profesorii pe orele zilei, pentru fiecare clasă mountHtoDay <- function(Z) { # 'tibble' <ord>prof|cls, split()-at pe clase # iniţializează octeţii de alocare, copiind tabloul global 'Bits' bith <- Bits # alocă pe orele 1..7, orele (lecţiile) unei clase mountHtoCls <- function(Q) { # 'Q' conţine liniile din Z cu o aceeaşi 'cls' # cat(Q$cls[1], " ") ## dacă vrem să vedem clasele tratate pe parcurs mpr <- Pore[[nrow(Q)-3]] # matricea de permutări corespunzătoare clasei for(i in 1:ncol(mpr)) { po <- mpr[, i] S <- Q %>% mutate(ora = po) # etichetează cu permutarea curentă # vectorul octeţilor de ore asociaţi acestei permutări: bis <- bitwShiftL(1, S$ora - 1) # vectorul octeţilor de ore alocate deja profesorilor clasei: bhp <- bith[S$prof] # Dacă există suprapuneri (de ore) între cei doi vectori, # atunci angajează coloana următoare a matricei de permutări, # dacă mai există una (altfel, abandonează) if(i == ncol(mpr) & any(bitwAnd(bhp, bis) > 0)) { succ <<- FALSE return(NULL) } if(any(bitwAnd(bhp, bis) > 0)) next # se presupune că sunt cel mult 2 ore de profesor, la aceeaşi clasă j <- anyDuplicated(names(bhp)) if(j > 0) { # dacă în Z, profesorul are 2 ore la acea clasă bis[j-1] <- bis[j] <- bis[j-1] + bis[j] } # actualizează global, octeţii de alocare: bith[S$prof] <<- bitwOr(bhp, bis) return(S) } } succ <- TRUE # aplică montHtoDay() pentru fiecare clasă, în ordinea iniţială a claselor orar <- Z %>% map_df(., function(K) mountHtoCls(K)) while(succ == FALSE) { print("insucc") ## nu se poate trece de clasa curentă succ <- TRUE bith <- Bits # reiniţializează octeţii de alocare pe orele zilei orar <- Z %>% sample(.) %>% # ordonează aleatoriu lista tabelelor claselor map_df(., function(K) mountHtoCls(K)) # reia alocarea orelor } return(orar) # orarul zilei, prof|cls|ora } ## HELPER: orarofday <- function(sch, zi) { # după Schimb (1 sau 2) şi Zi ("Lu", etc.) tb <- readRDS(paste0("Dis", sch, "_", zi, ".RDS")) Bits <<- readRDS(paste0("Bits", sch, ".RDS")) # alocare 1..7 profesorilor din Schimb orZ <- mountHtoDay(tb) saveRDS(orZ, file=paste0("orar", sch, zi, ".RDS")) } Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") for(zi in Zile) { orarofday(1, zi) orarofday(2, zi) }
Lansând programul din consola R (prin source("set_hours_day.R")), rezultă pe rând fişierele "orar1Lu.RDS", "orar2Lu.RDS", ş.a.m.d. conţinând distribuţia pe orele 1..7 ale zilei pentru câte un schimb, pentru fiecare zi. Cum era de aşteptat – având mai puţin de 500 de ore pe schimb, pentru câte doar 16 clase la 60 de profesori – fiecare orar se obţin aproape instantaneu (în 4-6 secunde), cum se vede afişând timpii la care sunt înregistrate fişierele respective:
vb@Home:~/21apr/LRC/STMT$ ls -l -t --time-style=full-iso orar*.RDS 19:16:57.837249326 orar2Vi.RDS 19:16:54.461208473 orar1Vi.RDS 19:16:48.041130783 orar2Jo.RDS 19:16:43.793079375 orar1Jo.RDS 19:16:39.085022399 orar2Mi.RDS 19:16:30.472918173 orar1Mi.RDS 19:16:23.120829191 orar2Ma.RDS 19:16:19.584786393 orar1Ma.RDS 19:16:13.928717934 orar2Lu.RDS 19:16:08.380650780 orar1Lu.RDS
Cele 10 orare zilnice s-au obţinut deci între momentele de timp 19:16:00 şi 19:16:57, adică în mai puţin de un minut; este interesant că în toate cele 10 cazuri, tratarea a fost liniară: nu s-a schimbat (constatând "insucc" la una dintre clase, cum am avut în [1]) ordinea iniţială (alfabetică) a claselor.
Fiindcă rezultatul se obţine aşa de repede, am putea genera uşor un set cam cât vrem de mare de orare (eventual, numai pe o anumită zi şi un anumit schimb), schimbând aleatoriu ordinea iniţială a claselor – urmând să alegem din setul obţinut, acel orar care satisface anumite criterii (de exemplu, să aibă cât mai puţine ferestre); aici însă, ne abţinem să operăm astfel şi vom lucra pe primele orare obţinute.
Finalizarea în paralel, a orarelor schimburilor unei zile
În directorul /recast avem şi aplicaţia "dayRecast.html", prin care vom putea rearanja (interactiv) distribuţia pe orele 1..7 ale zilei (furnizată într-un element <textarea>); între timp, am formulat prin extindere şi "twoDaysRecast.html" (urmând să o adăugăm şi în /recast), prin care putem lucra „în paralel” pe ambele schimburi ale zilei – fiind astfel mai uşor de urmărit „legarea” orelor dintr-un schimb cu cele din celălalt schimb, la profesorii care au ore în ambele schimburi, în ziua respectivă.
Dar mai întâi, avem de transformat „formatul” prof|cls|ora specific pentru fişierele orar*.RDS obţinute mai sus, într-un fişier CSV cu structura generică "prof, ora1, ora2, ..., ora7" (care să fie apoi „pastat” în elementul <textarea> al aplicaţiei):
# rds2csv.R (orar*.RDS ==> orar*.CSV, ordonat alfabetic) library(tidyverse) file <- "orar" Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") format_csv <- function(sch, zi) { readRDS(paste0(file, sch, zi, ".RDS")) %>% split(.$prof) %>% map_df(., function(Q) spread(Q, ora, cls)) %>% mutate(prof = as.character(prof)) %>% arrange(prof) } for(zi in Zile) for(sch in 1:2) { orz <- format_csv(sch, zi) write_csv(orz, file=paste0(file, sch, zi, ".CSV"), na = "-", col_names=FALSE) }
Pentru a lucra „în paralel” pe cele două schimburi, am transformat $prof în 'character' (era 'factor', ordonat după numărul de ore ale profesorului pe ziua respectivă) şi am ordonat alfabetic; /dayRecast cere fişier CSV fără antet, deci l-am omis (folosind în write_csv() opţiunea col_names).
Iată o imagine parţială a aplicaţiei /dayRecast, după ce am înscris în elementele <textarea> fişierele CSV pentru cele două schimburi din ziua "Vi":
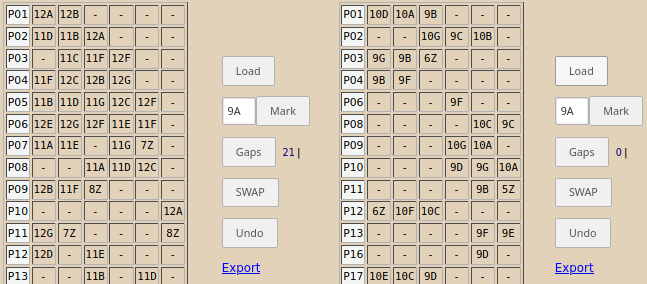
În panoul din dreapta este redat de fapt nu fişierul orar2Vi.CSV iniţial, ci rezultatul unei serii de operaţii SWAP (de vreo 30 minute) prin care am reuşit să reducem numărul ferestrelor de la 20 cât erau iniţial, la 0. Nu este greu de redus numărul ferestrelor pe fiecare schimb în parte, dar de legat orele din primul schimb cu cele din al doilea este posibil în cel mult jumătate din cazuri; foarte probabil, va trebui din când în când să mai mutăm (cumva) clase dintr-o zi în alta, pentru a putea creşte numărul legărilor de ore între cele două schimburi (sau pentru a le evita).
De exemplu, în situaţia din imaginea de mai sus, la "P02" cele 3 ore din primul schimb nu pot fi „legate” cu cele din al doilea schimb, acestea fiind plasate începând cu a 3-a oră; "P01" şi "P03" sunt cazuri fericite: orele lor din primul schimb sunt şi la unele clase care au câte 6 ore pe zi şi pot fi mutate spre ultima oră (legându-le astfel de cele plasate lor începând cu ora 1, în al doilea schimb).
Obs. Desigur, ar fi de rescris "dayRecast.js", pentru a avea un singur set de butoane (nu două „identice”, cum se vede mai sus), acţionând pe un schimb sau pe celălalt în funcţie de un anumit context (dependent de schimb).
Am finalizat prin operaţii SWAP orarele pe Vi, plecând de la situaţia de pe care am redat imaginea de mai sus (cam într-o oră, trebuind să mai operez şi pe schimbul al doilea); prin Export am obţinut fişierele extVi1.csv şi extVi2.csv, le-am adăugat câte un antet (cu "a" de la A.M. şi "p" de la P.M. ca prefix pentru orele din schimburile respective) şi folosind full_join(), am reunit datele din aceste fişiere într-un acelaşi obiect 'tibble':
# exportCSV2df.R (reuneşte orarele CSV a schimburilor unei zile, în acelaşi 'tibble') library(tidyverse) S1 <- read_csv("extVi1.csv") S2 <- read_csv("extVi2.csv") S12 <- full_join(S1, S2) %>% replace(is.na(.), "-") %>% arrange(prof) print(S12, n=Inf) # A tibble: 47 x 13 prof a1 a2 a3 a4 a5 a6 p1 p2 p3 p4 p5 p6 1 P01 - - - - 12A 12B 10A 10D 9B - - - 2 P02 - - - 12A 11D 11B 9C 10G 10B - - - 3 P03 - - - 11F 11C 12F 9B 9G 6Z - - - 4 P04 - - 12B 12C 12G 11F - - - - 9F 9B 5 P05 11D 12F 12C 11B 11G - - - - - - - 6 P06 11F 12G 12E 12F 11E - - - - - - 9F 7 P07 11A 11G 11E 7Z - - - - - - - - 8 P08 - - - 11D 12C 11A 10C 9C - - - - 9 P09 - - - 12B 11F 8Z 10G 10A - - - - 10 P10 12A - - - - - - - - 9G 9D 10A 11 P11 - - - 12G 8Z 7Z 5Z 9B - - - - 12 P12 - - - - 12D 11E 10F 6Z 10C - - - 13 P13 - - - - 11B 11D 9E 9F - - - - 14 P14 8Z 7Z 11G 11C - - - - - - - - 15 P15 - 8Z 12A 11G 12E - - - - - - - 16 P16 - - - 11A 12F 12G 9D - - - - - 17 P17 - - - - - - - - 10E 9D 10C - 18 P18 - - 11D - - - - - - 10C 9C 10D 19 P19 - 11E 11F - - - - - - 9B - - 20 P20 12D 12B - - - - - 10F 5Z - - - 21 P21 11E - - - - - - - - 9E 10E - 22 P22 - - - - 11A 12C 10D - - - - - 23 P23 - - - 11E 7Z 12E 6Z 10E 9G - - - 24 P24 - - - - 12B 12A 9F 9E - - - - 25 P25 - - - - - 11C 10B 9A 9D - - - 26 P26 7Z 12D 11B - - - - - - - - - 27 P27 - 11C 12D - - - - - - - 9A 10B 28 P28 - - 12F 12E - - - - 9A 10B 9G 9C 29 P29 - - - - - - - 9D 10G 10D - - 30 P30 11G 11D - - - - - - 9F 10F - - 31 P31 - - 7Z 8Z - - - - - - 10D 10C 32 P32 - 11A 11C - - - - - 9E 9C 10A - 33 P33 - 12C 8Z 12D - - - - - - - - 34 P34 - - - - - - - - - 9A 10G 9G 35 P35 - 11F 12G - - - - - - 10G 9B - 36 P36 12C 12E - - - - 9G - - - - - 37 P37 11C 12A 11A - - - - - - - - - 38 P38 - - - - - - 9A 10B 9C 5Z - - 39 P39 - 11B - - - - - - 10A 6Z - - 40 P40 - - - - - - - 10C 10D 10A 10B - 41 P41 - - - - - - 10E 5Z 10F - - - 42 P43 - - - - - - - - - 9F 9E 10E 43 P49 12F - - - - - - - - 10E 10F - 44 P52 - - - - - - - - - - 5Z 6Z 45 P55 - - - - - - - - - - 6Z 5Z 46 P59 12B - - - - - - - - - - - 47 P60 - - - - - - - - - - - 9E
Şi pe primul şi pe al doilea schimb, avem câte zero ferestre; dar n-am reuşit decât în 13 cazuri din cele 29 existente, să legăm orele din primul schimb de cele din al doilea – şi aceasta, decizând ca trei clase care au câte doar 5 ore (anume, 11B, 12E şi 12G) să înceapă de la a doua oră din zi.
Totuşi, am urmărit un principiu oarecum compensatoriu: dacă schimburile nu pot fi „legate”, atunci distanţa dintre ele să fie cât se poate de mare (de măcar 3 ore), încât profesorul respectiv să nu stea degeaba între cele două schimburi (că de obicei, într-o fereastră de una sau de două ore asta faci: „omori timpul”, aşteptând să treacă).
De exemplu, "P06" îşi încheie primul schimb la ora a 6-a şi îl începe pe al doilea peste 4 ore; zicem că o asemenea distanţă între schimburi nu ar trebui considerată ca „fereastră”! În toate cazurile, distanţa dintre schimburi este suficient de mare pentru a permite profesorului să nu stea degeaba între schimburi; practic, orarul redat mai sus are zero ferestre.
La prima vedere s-ar părea că putem face mai mult, până să ne mulţumim cu „principiul compensatoriu” exprimat mai sus: la profesorii care au câte o singură oră într-un schimb, la distanţă faţă de orele pe care le au şi în celălalt schimb (cum avem mai sus pe liniile 6, 10, 18, 19, 36, 39 şi 43), putem căuta să mutăm ora respectivă într-o altă zi (aducând în loc, oră la aceeaşi clasă unui alt profesor).
Dar această idee este aplicabilă numai dacă în ziua în care vrem să mutăm clasa, profesorul respectiv nu are deja alocată o oră la acea clasă; la "P06" putem muta 9F într-o altă zi, fiindcă "P06" are în încadrare o singură oră la această clasă; la "P10" încă putem muta 12A, dar numai în anumite două zile – fiindcă "P10" este încadrat pe 3 ore la clasa respectivă şi bineînţeles că aceste 3 ore trebuie alocate în zile diferite (şi nu toate într-o aceeaşi zi, sau numai în două zile); însă "P19" de exemplu, are în încadrare 4 ore la 9B, iar găsirea zilei în care să o mutăm devine dificilă; iar la "P39" chiar nu putem muta 11B într-o altă zi, fiindcă acesta are la 11B un număr de 5 ore pe săptămână (obligând la plasarea lor câte una, în fiecare zi).
Rezultă această orientare practică (neobligatorie): vizăm întâi (prin operaţii SWAP) legarea schimburilor la acei profesori care au o singură oră într-unul dintre schimburi şi abia apoi, căutăm să legăm schimburile (în măsura în care mai este posibil) şi celorlalţi (urmărind simultan, să reducem ferestrele). M-am ghidat după acest principiu de lucru, pentru ziua Jo, obţinând cam într-o oră de lucru acest orar (în care, dintre clasele care au câte 5 ore, 12ACF şi 11C încep programul de la a doua oră din zi – altfel nu prea putem lega schimburile între ele):
# A tibble: 48 x 13 prof a1 a2 a3 a4 a5 a6 p1 p2 p3 p4 p5 p6 1 P01 - - - 11D 12B 11A 9B 10A 9D - - - 2 P02 - - - 12A 11D 11B 10F 10B - - - - 3 P03 - - - 12E 11B 12F - 9F 9B 9G - - 4 P04 - - - 11E 12G 12D 9D 10G 9E - - - 5 P05 11B 11E 12C - - - - - - - 9C 9A 6 P06 7Z 11G - - - - - - - - - - 7 P07 11G 11A 11E - - - - - 10A 10E - - 8 P08 - - - - 11A 12C 10C 9C 10D - - - 9 P09 12E 12G 11D 11B 11E - - - - - - - 10 P10 - - - - - 12A 10A 9G 10F - - - 11 P11 - - - - 8Z 7Z 5Z 9B - - - - 12 P12 11E 11F - - - - - - - 5Z - - 13 P13 - - - - - 8Z 10D 9E - - - - 14 P14 - 12A 11C 11G 7Z - - - - - - - 15 P15 - - 12B 8Z 12E 11G 9F - - - - - 16 P16 - - 12G 11A 12F - 9A 9D - - - - 17 P17 12B - - - - - - - 10C 9B 9G - 18 P18 - - - - - 11D 9C 10C 10G 10D - - 19 P19 - - - - - - - - 10E 9F 10G 9B 20 P20 - - - 12D - - 6Z 5Z - - - - 21 P21 - - - - - 11E 9E 10E 9F - - - 22 P22 - 12C 12A - - - - - - 9A 9E 10D 23 P23 - 12E 11B - - - - - - 6Z - - 24 P24 - 12D 11F 12B 12A - - - - - - - 25 P25 - - - - - 11C 10B 9A 9G - - - 26 P26 12G 7Z - - - - - - - - 5Z 10B 27 P27 - - 11A 11C 12D - - - - - 10C - 28 P28 - - - 12F 11C 12E 9G - - - - - 29 P29 12D - - - - - - - - - 9D 10A 30 P30 - - - - - - - - 5Z 10F 9F 9D 31 P31 - 8Z 7Z - - - 10E 6Z - - - - 32 P32 11A 11C 12F - - - - - - - - - 33 P33 8Z 12B - - - - - - 9C 9D - - 34 P34 11D - - - - - - - 9A 10B - - 35 P35 - - 12D 12G 11F - - - - - - - 36 P36 - - 12E 12C - - - - - - - 9G 37 P37 - - 11G 11F 12C - - - - - - - 38 P38 - - - - - - - - 10B 9C 9A 9F 39 P39 - 11B - - - - - - - - 10A 10G 40 P40 - - - - 11G 11F 10G 10F - - - - 41 P46 - - - - - - - - - 9E - - 42 P48 - - - - - - - - - 10G 10E 10F 43 P49 - 12F - - - - - - - - 10F 10E 44 P51 - - - - - - - - - - 10D 10C 45 P54 11F 11D - - - - - - - 10A 10B - 46 P55 - - 8Z 7Z - - - - - - - - 47 P57 - - - - - - - 10D 6Z 10C - - 48 P58 - - - - - - - - - - 9B 9C
Iarăşi, am obţinut zero ferestre pe fiecare schimb în parte.
Dintre cei 48 de profesori care au ore Jo, 15 au ore (fără nicio fereastră) într-un singur schimb; 13 au ore în ambele schimburi, legate:
> S12[S12$a6 != '-' & S12$p1 != '-', ] # A tibble: 13 x 13 prof a1 a2 a3 a4 a5 a6 p1 p2 p3 p4 p5 p6 1 P01 - - - 11D 12B 11A 9B 10A 9D - - - 2 P02 - - - 12A 11D 11B 10F 10B - - - - 3 P04 - - - 11E 12G 12D 9D 10G 9E - - - 4 P08 - - - - 11A 12C 10C 9C 10D - - - 5 P10 - - - - - 12A 10A 9G 10F - - - 6 P11 - - - - 8Z 7Z 5Z 9B - - - - 7 P13 - - - - - 8Z 10D 9E - - - - 8 P15 - - 12B 8Z 12E 11G 9F - - - - - 9 P18 - - - - - 11D 9C 10C 10G 10D - - 10 P21 - - - - - 11E 9E 10E 9F - - - 11 P25 - - - - - 11C 10B 9A 9G - - - 12 P28 - - - 12F 11C 12E 9G - - - - - 13 P40 - - - - 11G 11F 10G 10F - - - -
iar dintre aceştia, 7 au câte o singură oră într-unul dintre cele două schimburi.
9 profesori au unica oră dintr-un schimb nelegată de orele pe care le au în celălalt schimb. 7 profesori au câte cel puţin două ore în fiecare schimb, iar orele din primul schimb sunt distanţate faţă de cele din al doilea; doi profesori ("P03" şi "P16") au ore în ambele schimburi, cu câte o fereastră (de o singură oră) între schimburi; "P20" are o fereastră de două ore între schimburi.
Pe lângă situaţiile enumerate mai sus, care se pot constata direct pe orarul redat, avem un caz „invizibil” de care chiar am uitat: "P06" este cuplat cu "P48" pe clasele 10GEF – încât iată că mai apare un caz de „ore în ambele schimburi, nelegate” şi dispare unul de la „ore într-un singur schimb”.
Am lucrat analog şi orarele pentru Mi, urmărind de data aceasta şi un alt aspect: profesorul care are un anumit dezavantaj în orarul unei zile, să nu-l mai aibă şi într-o altă zi (ceea ce este posibil de obţinut în ceea ce priveşte ferestrele propriu-zise – de o oră – dar nu poate reuşi decât în puţine cazuri care ar necesita eliminarea distanţării existente între orele dintr-un schimb şi cele din celălalt schimb).
Orarele obţinute pentru Mi (ne abţinem să le mai transcriem aici) au şi ele, caracteristicile redate deja mai sus (zero ferestre în primul schimb, zero ferestre în al doilea; 9 profesori cu ore în ambele schimburi, nedistanţate; 17 profesori cu ore în ambele schimburi, distanţate; etc.); în plus, profesorul "P03" de exemplu, care Jo avea o fereastră de o oră între schimburi – are acum ore tot în ambele schimburi, dar legate (urmărind ca „dezavantajul” produs Jo să nu se repete într-o altă zi).
Cum se poate mai bine de atât…
De fapt, pe noi nu ne interesează orarul ca „produs final”, ci doar punerea la punct a programelor R redate mai sus şi a aplicaţiilor interactive asociate, prin care obţinem un orar acceptabil în principiu.
Iar ce putem noi să facem, pentru a produce un orar mai bun, constă în a o lua de la capăt: revenim în aplicaţia /recast şi folosim SWAP pentru a reduce cât mai mult situaţiile în care profesorul vine într-o aceeaşi zi în ambele schimburi; apoi reluăm generarea prin R a orarelor zilnice, pentru noua distribuţie pe zile obţinută şi reluăm în sfârşit, lucrul interactiv în /dayRecast, pentru a reduce cât mai mult ferestrele şi a regla eventual, distanţele dintre schimburi.
Cu învăţămintele dobândite în experienţa precedentă, cu siguranţă că luând-o de la capăt vom reuşi un orar „mai bun” (iar în experienţele viitoare, ne vom mulţumi pentru efortul făcut acum).
Pe de altă parte, să observăm că datele de furnizat unui program care produce orarul, nu sunt „date brute”, ci sunt create de cineva: iniţial, în baza unui anumit plan-cadru general, directorul şcolii atribuie anumite clase, pe câte un anumit număr de ore, profesorilor şcolii şi unora din afara şcolii. Nu cumva şi cel care furnizează datele, ar trebui să aibă grijă de calitatea şi contextul datelor pe care le constituie?
De obicei, directorul şcolii face încadrarea profesorilor pe clase fără a se gândi şi la problemele puse de implementarea încadrării respective într-un orar şcolar (care trebuie să corespundă şi unor criterii care ţin probabil de pedagogie şi de obiective didactice coerente, nu doar unor normative salariale şi unor pretenţii individuale); dar măcar, poate lămuri tuturor celor implicaţi în activitatea de zi cu zi a şcolii, de la bun început, unele principii (de bun-simţ, în fond) care urmează să fie respectate în construcţia orarului.
Dacă unui profesor i se dau multe clase într-un schimb, iar în celălalt schimb i se dă o singură clasă 9F să zicem, care are 3-4 ore pe disciplina respectivă – atunci acelui profesor trebuie să i se precizeze din start, două lucruri ne-negociabile: în primul rând, (având în vedere interesele elevilor) cele 3-4 ore la 9F trebuie făcute câte una pe zi; în al doilea rând – (ţinând seama şi de ceilalţi profesori) este puţin probabil ca orele din primul schimb să poată fi legate cu ora 9F din al doilea schimb şi cel mai probabil, distanţa dintre schimburi va fi de cel puţin 3 ore (evitând o fereastră inutilizabilă).
Iar dacă profesorul are câte cel puţin două clase şi într-un schimb şi în celălalt – atunci trebuie să i se precizeze din start că este puţin probabil ca în fiecare zi, cele două schimburi ale sale să poată fi legate între ele şi cel mai probabil, vor fi separate printr-un interval suficient de larg pentru a permite profesorului să nu piardă timpul între schimburi; desigur, va fi posibil, dar nu sigur, ca în unele zile să aibă ore numai într-un schimb; şi desigur, se va căuta ca un „defect” produs într-o zi unui profesor, să nu se repete şi într-o altă zi aceluiaşi profesor.
Asemenea explicitări (altfel, de bun-simţ) au desigur şi importanţă strategică: se previn obişnuitele nemulţumiri individuale şi contestări; orarul şcolii este oglinda activităţii de zi cu zi a şcolii, activitate care bineînţeles că trebuie să corespundă anumitor standarde (care nu prea au de-a face cu pretenţiile individuale).
Elaborarea orarului şcolar („oglinda” activităţii didactice din şcoală) nu începe cu „introducerea datelor” în "ascTimetables" (de exemplu), ci ar trebui să înceapă mai dinainte, din etapa încadrării profesorilor pe discipline şi clase (şi poate chiar mai dinainte, fiindcă încadrarea pe anul curent trebuie să aibă în vedere şi pe cea din anul precedent).
vezi Cărţile mele (de programare)