Din punctul unitar $\boldsymbol{z=\mathrm{e}^{i\theta}}$ (de argument $\theta$) se obține, prin translație spre dreapta cu o unitate, punctul $z+1$, din care prin rotire cu unghiul polar $\theta$, rezultă punctul $\boldsymbol{z(z+1)}$. Am arătat în [1], că $z(z+1)$ trasează o trisectoare Pascal ($\boldsymbol{\mathcal{P}}$), cu vârful în $O$ (cu această interpretare: locul parametrului complex $p$ al ecuației $z^3+pz+q=0$ cu o rădăcină fixată şi o a doua mobilă pe un acelaşi cerc cu centrul în origine este o trisectoare Pascal, cu axa de simetrie dată de dublul direcţiei rădăcinii fixe):

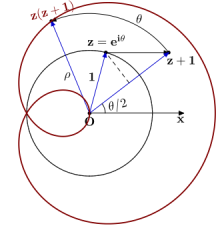
Obs. $\boldsymbol{z(z-1)}$ (când translația s-ar face spre stânga) generează aceeași curbă ca și $z(z+1)$).

Cum se vede ușor pe figură, avem $\rho=|z+1|=2\cos\frac{\theta}{2}$, iar unghiul polar al lui $z(z+1)$ este $\frac{3\theta}{2}$. Deci pentru punctele lui $\boldsymbol{\mathcal{P}}$ avem reprezentarea parametrică (polară):

$$(\boldsymbol{\mathcal{P}}): \,\,\boldsymbol{p(\theta)={2\cos\frac{\theta}{2}\,\,\left(\cos\frac{3\theta}{2}+i\sin\frac{3\theta}{2}\right)}},\,\theta\in(-\pi,\pi]\tag{1}$$

În Legăturile ecuației cubice am arătat că locul punctelor $\sqrt{p(\theta)\boldsymbol{+1}\,}$ — adică locul punctelor critice ale polinoamelor $f(z)=z^3+pz+q,\,z\in\mathbb{C},\,(p,q\in\mathbb{C})$ cu o rădăcină de modul 1 fixată — este format din două lemniscate Booth coaxiale; acum, reluând [2], ne ocupăm de punctele $\boldsymbol{\sqrt{p(\theta)\,}}$ — cu alte cuvinte, studiem curba $\boldsymbol{\mathcal{Q}}$ rezultată aplicând lui $\boldsymbol{\mathcal{P}}$ radicalul față de $O$; mai jos, reperăm radicalii la vârful $O$ al lui $\boldsymbol{\mathcal{P}}$.
Fiindcă prin radical, unghiul polar se înjumătățește, avem imediat:

$$(\boldsymbol{\mathcal{Q}}): \,\,\boldsymbol{q(\theta)=\sqrt{p(\theta)\,}=\pm\,\sqrt{2\cos\frac{\theta}{2}\,}\left(\cos\frac{3\theta}{4}+i\sin\frac{3\theta}{4}\right)},\,\theta\in(-\pi,\pi]\tag{2}$$

Este important (când am produce graficul) să menținem $\theta$ în intervalul $\boldsymbol{(-\pi, \pi]}$ (și nu de la $0$ la $2\pi$) — pentru a avea $\cos \frac{\theta}{2}$ pozitiv. În figura următoare avem o "verificare" practică: am trasat punct cu punct graficele $Q^{\boldsymbol{+}}$ (cu negru) și $Q^{\boldsymbol{-}}$ (cu albastru), corespunzătoare semnului din fața radicalului din (2) și apoi am trasat (cu roșu) pătratele punctelor lui $Q$ (constatând $Q^{\boldsymbol{2}}=P$, adică $P=\sqrt{Q\,}$); pointând crescător intervalul $[-\pi,\,\pi]\ni\theta$, trasarea a plecat (punct după punct) în fiecare caz, din origine (respectiv, după cei trei vectori tangenți marcați pe figură):

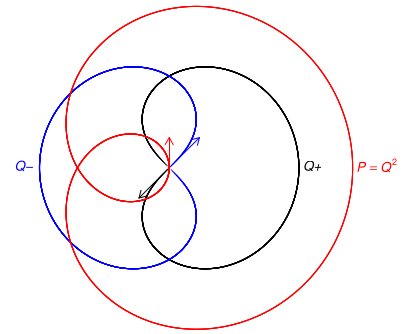
$Q^{\boldsymbol{+}}$ și $Q^{\boldsymbol{-}}$ apar simetric față de axa $Oy$ și este suficient să investigăm doar "ramura" $Q^{\boldsymbol{+}}$ a lui $\boldsymbol{\mathcal{Q}}$.

Obs. Radicalul complex de ordinul doi are două valori, pe care în (2) le-am deosebit prefixând cu "$\pm$", cum se obișnuiește… De fapt, acest "$\pm$" maschează cumva, "adevărul": raza polară este $\sqrt{\cos\frac{\theta}{2}}$ (fără "$\pm$"), iar deosebirea celor două valori ale radicalului apare la argument — "înjumătățim unghiul polar" din (1) și avem astfel (2), respectiv "înjumătățim și adăugăm $\boldsymbol{\pi}$", obținând a doua valoare a radicalului, în care argumentul este $(\boldsymbol{\frac{3\theta}{4} + \pi})$. Subliniem că în ambele cazuri — folosind "$\pm$", respectiv plotând o dată cu argumentul $\frac{3\theta}{4}$ și apoi cu $(\frac{3\theta}{4} + \pi)$ — rezultă aceleași grafice, pentru $Q^{\boldsymbol{+}}$ și respectiv $Q^{\boldsymbol{-}}$. Totuși… pentru a plota complet $Q$, în toate cadranele, tot trebuie să schimbăm semnele coordonatelor; acesta este defectul major al reprezentărilor parametrice neraționale: nu putem considera "deodată", întreaga curbă.

Unele constatări sunt simplu de făcut și folosind direct forma polară (2). Intersecția lui $\mathcal{Q}^{\boldsymbol{+}}$ cu $Ox$ are unghiul polar $0$, deci este punctul $(\sqrt{2},\,0)$; dar trebuie să recunoaștem că a găsi la fel (fără a miza pe simetria față de $O$) intersecția opusă, devine cam complicat: argumentul $3\theta/4$ ar trebui să corespundă unghiului polar $\pi$, însemnând că $\theta$ ar fi $4\pi/3\gt \pi$ și avem de întâmpinat anumite "subtilități" pentru a stabili astfel, răspunsul corect $(-\sqrt{2\,},\,0)$…
Obs. Practic, când producem graficul, nu avem de-a face cu "subtilități" (teoretice): se calculează valorile pentru $Q\boldsymbol{+}$ și apoi, doar li se schimbă semnul, pentru a plota și $Q\boldsymbol{-}$.

Poate ar fi mai comod, sau mai simplu, de lucrat cu o formă carteziană? poate cu o parametrizare mai obișnuită (dacă există), în loc de forma polară (2) ?

Observăm că $x^2+y^2=2\cos\frac{\theta}{2}=4\cos^2\frac{\theta}{4}-2$ și avem exprimarea $\cos\frac{3\theta}{4}=$
$=(4\cos^2\frac{\theta}{4}-3)\cos\frac{\theta}{4}=(x^2+y^2-1)\,\cos\frac{\theta}{4}$. Fiindcă $x=\pm\sqrt{2\cos\frac{\theta}{2}\,}\cos\frac{3\theta}{4}$, rezultă: $$x^2=\frac{1}{4}\,(x^2+y^2)\,(x^2+y^2-1)^2\,(x^2+y^2+2)\tag{*}$$ de unde, cu un calcul elementar, ajungem la această "rescriere" carteziană a lui (2):

$$(\boldsymbol{\mathcal{Q}}):\,\,\boldsymbol{(x^2+y^2)^4 - 3(x^2+y^2)^2 - 2(x^2-y^2) = 0}\tag{3}$$

Obs. De pe figura de mai sus ne putem da seama că intersecția lui $\boldsymbol{\mathcal{Q}}$ cu o dreaptă (ignorând tangentele) poate avea două, patru, sau cel mult șase puncte; ajungem și la opt (gradul ecuațiai (3)), observând că $O$ este totuși un punct "special" — argumentul corespunzător lui în (2) fiind nedeterminat — și probabil, trebuie considerat ca "punct multiplu"….

Pe de altă parte, (*) sugerează o parametrizare (irațională) ușor de calculat, față de raza vectoare $\rho=\sqrt{x^2+y^2}\,$ (renotată ca parametru cu $t$):

$$(\boldsymbol{\mathcal{Q}}):\,\,\begin{array}{l} \boldsymbol{x = x(t) = \pm\,\,\frac{1}{2}\,t(t^2-1)\,\sqrt{2+t^2\,}}\\ \boldsymbol{y = y(t) = \pm\,\frac{1}{2}\,t(t^2+1)\,\sqrt{2-t^2\,}} \end{array}\quad \boldsymbol{t\in[\,0,\,\sqrt{2\,}\,]}\tag{4}$$

Cum se vede din (3), $\boldsymbol{\mathcal{Q}}$ este simetrică față de axe (dar schimbând $(x,y)$ cu $(y,x)$, graficul va fi rotit cu $90^\circ$); deci ar fi (sau pare a fi) suficient să ne ocupăm de porțiunea $Q^\boldsymbol{+}$ — pentru care păstrăm $x(t)$ cu semnul ei, fără "$\pm$" în față — și de fapt, de partea sa $Q^\boldsymbol{+}_1$ aflată deasupra axei $Ox$ (pentru care și $y(t)$ are semnul propriu, fără "$\pm$" în față). Pentru porțiunea $Q^\boldsymbol{+}_1$ avem:

$$\begin{array}{l} \dfrac{dx}{dt} = \dfrac{2t^4+2t^2-1}{\sqrt{2+t^2}}\\ \dfrac{dy}{dt} = \dfrac{-2t^4+2t^2+1}{\sqrt{2-t^2}},\,\,t\in[0,\sqrt{2\,})\\ \dfrac{dy}{dx} = \dfrac{-2t^4+2t^2+1}{2t^4+2t^2-1}\sqrt{\dfrac{2+t^2}{2-t^2}}, \,\,t\in[0,\,\sqrt{2\,})-\sqrt{\frac{\sqrt{3\,}-1}{2}} \end{array}\tag{5}$$

Din (4), pentru $t=\sqrt{2}$, respectiv $t=1$, găsim intersecțiile cu axele — punctele $\boldsymbol{A}(\sqrt{2}, 0)$ și $\boldsymbol{B}(0,1)$ (împreună cu opusele acestora). Din (3), pentru $x^2=y^2$ găsim intersecțiile cu bisectoarele lui $xOy$ — punctul $\boldsymbol{C}\left(\sqrt{\sqrt{3\,}/2\,},\,\sqrt{\sqrt{3\,}/2\,}\right)$ împreună cu simetricele sale față de $xOy$ (constituind vârfurile unui pătrat înscris în $\boldsymbol{\mathcal{Q}}$).

Pentru $t\in(0,\sqrt{2})$, funcția $x'(t)$ are un minim în $t_1=\sqrt{\frac{\sqrt{3}-1}{2}}\approx 0.605$ — deci $Q^{\boldsymbol{+}}$ este cuprinsă între abscisele $x(t_1)=-\frac{1}{8}(3-\sqrt{3})\sqrt{2\sqrt{3}\,}\approx -0.295$ și $\sqrt{2}$. Să observăm că $\frac{dy}{dx}(t_1)=\infty$, deci în punctul $\boldsymbol{D}\left(x(t_1),\,y(t_1)=\frac{1}{8}(\sqrt{3}+1)\sqrt{2(3\sqrt{3}-4)\,}\approx 0.528\right)$ (și în simetricul vertical al acestuia) $Q^{\boldsymbol{+}}$ are tangentă verticală.
Iar $y'(t)$ are un maxim în $t_2=\sqrt{\frac{\sqrt{3}+1}{2}}\approx 1.168$ — deci $Q^{\boldsymbol{+}}$ este cuprinsă pe verticală între $y(t_2)=\frac{1}{8}(3+\sqrt{3})\sqrt{2\sqrt{3}\,}\approx 1.1009$ și $-y(t_2)\approx -1.1009$. Fiindcă $\frac{dy}{dx}(t_2)=0$, urmează că în punctul $\boldsymbol{E}\left(x(t_2)=\frac{1}{8}(\sqrt{3}-1)\sqrt{2(3\sqrt{3}+4)\,}\approx 0.392,\,y(t_2)\right)$, ca și în simetricul vertical al acestuia, $Q^{\boldsymbol{+}}$ are tangentă orizontală.

Subliniem că exprimările de mai sus pentru $D$ și $E$ pot fi "simplificate", până la forma găsită deja (dar pe altă cale) în [2]:
$\boldsymbol{E}=\frac{1}{4}\left(\sqrt{2\sqrt{3\,}-1\,},\, \sqrt{6\sqrt{3\,}+9\,}\right)$, iar $\boldsymbol{D}=\frac{1}{4}\left(-\sqrt{6\sqrt{3\,}-9\,},\,\sqrt{2\sqrt{3\,}+1\,}\right)$

Sintetizăm datele stabilite mai sus, adăugând și tangentele în $B$ și $C$:

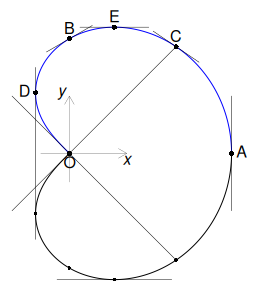
Tangenta în $B$ are panta $\frac{dy}{dx}(t=1)=\frac{\sqrt{3}}{3}$.
Din $x(t)=y(t)$ găsim că punctul $C$ se obține pentru $t=\sqrt[4]{3}\approx 1.316$, deci panta tangentei în $C$ este $\frac{dy}{dx}(t=\sqrt[4]{3})=\frac{3\sqrt{3}-14}{13}\approx -0.677$; rezultă desigur, că tangenta în $C$ nu este paralelă cu a doua bisectoare — altfel, calculul făcut mai sus pentru panta ei pare inutil… Și totuși, nu este inutil: indicând numai cele 6 puncte marcate pe figură și pantele tangentelor, le putem lega prin curbe Bézier, trasând astfel, cu suficientă exactitate, toate punctele lui $Q^{\boldsymbol{+}}_1$ — v. Metafont pentru trisectoarea lui Pascal.

Ar mai fi de adăugat că în origine, $Q^{\boldsymbol{+}}$ are ca "semitangente", bisectoarele lui $xOy$. Astfel, putem considera că am încheiat cu "reprezentarea grafică" a curbei; am evidențiat marginile și punctele importante și simetrizând față de $Oy$ avem imaginea întregii curbe $\boldsymbol{\mathcal{Q}}$. Dar… ce semnificație sau însemnătate are această curbă, afară de faptul că este radicalul față de vârf al trisectoarei lui Pascal?
Pentru orice curbă, putem vorbi de pătratul și de radicalul ei, astfel că problema adevărată este aceea de a încadra $\boldsymbol{\mathcal{Q}}$ în vreo categorie cunoscută de curbe, sau de a defini $\boldsymbol{\mathcal{Q}}$ în modul obișnuit, ca "loc geometric".

$\boldsymbol{\mathcal{Q}}$ seamănă (subliniem, doar seamănă) cu o pereche de cardioide cu nodul în $O$, simetrice față de $Oy$; dar $\boldsymbol{\mathcal{Q}}$ nu satisface vreuna (probabil, niciuna) dintre proprietățile cardioidei — cel mai simplu exemplu de diferență: cardioida este tangentă în $O$ axei $Ox$, în timp ce $\boldsymbol{\mathcal{Q}}$ are ca tangente în $O$ bisectoarele lui $xOy$.
Iar "diferența" este chiar mare, cum se vede adăugând pe figura precedentă, cu roșu, cardioida $\boldsymbol{\rho=\frac{\sqrt{2}}{2}(1+\cos\varphi)}$ cu nodul $O$ și cu același vârf $A$ ca și $\boldsymbol{\mathcal{Q}}$; am reprezentat cu "magenta", curba dată de diferența razelor vectoare ale punctelor lui $\boldsymbol{\mathcal{Q}}$ și respectiv, ale cardioidei, de același unghi polar (făcând în (2) $\frac{3\theta}{4}=\varphi$):

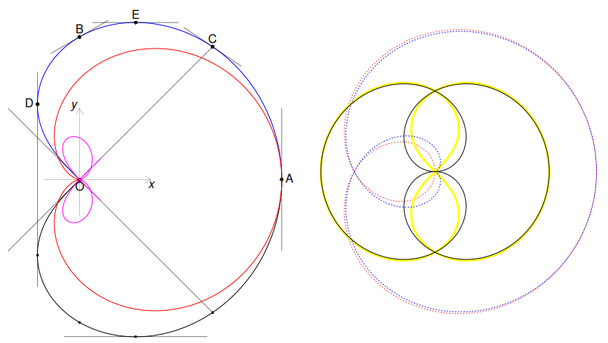
$\boldsymbol{\mathcal{Q}}$ ar semăna cel mai mult, cu foliul lui Dürer $\boldsymbol{\frac{\sqrt{2}}{2}(\mathrm{e}^{i\varphi/2}+\mathrm{e}^{3i\varphi/2})}$, reprezentat mai sus în dreapta, cu linie neagră subțire; linia galbenă (mai groasă) reprezintă $\boldsymbol{\mathcal{Q}}$ și se vede că liniile (negru și galben) aproape coincid pe porțiunea din afara celor două bucle prin origine (dar aceste bucle diferă categoric, între cele două curbe).
Pentru a deduce suplimentar, diferența între cele două curbe — am plotat punctat și pătratele lor: cu puncte roșu, $\boldsymbol{\mathcal{Q}^2}$ (deci o trisectoare Pascal), iar cu puncte-"blue" pătratul foliului Dürer (de recunoscut, uitându-ne în urmă, pe la Puterile cercului, ca fiind… puterea 5 a unui cerc dus prin origine).

Având în vedere apropierea semnalată mai sus, propunem pentru curba $\boldsymbol{\mathcal{Q}}$, denumirea nah_Dürer-folium (a vedea "nah", în germană); iar notația mai adecvată ar fi ($\boldsymbol{\mathfrak{D}}$)…

Obs. Dacă am recunoaște curba "magenta" rezultată mai sus, atunci am avea o definiție punctuală pentru $\boldsymbol{\mathfrak{D}}$: locul punctelor $P$ pentru care $PQ=OR$, unde $Q$ și $R$ sunt intersecțiile cu cardioida și respectiv, cu acea curbă "magenta", ale razei vectoare $OP$…

Unele tatonări directe

$\boldsymbol{\mathfrak{D}}$ este dată prin ecuațiile (echivalente) (2), (3) sau (4) și… încă nu știm nimic despre proprietățile geometrice ale ei; poate vom reuși la un moment dat, să definim $\boldsymbol{\mathfrak{D}}$ ca "loc geometric" — dar deocamdată, ce putem face acum este ceva de natură mecanică: să calculăm.
Reproducem aici rezultatele pentru derivatele funcțiilor din (4) ($\overset{\boldsymbol{.}}{x}(t)$ etc.; folosim notația lui Newton, cu punct în loc de accent); precizăm că (pentru tatonare) am vizat numai porțiunea curbei aflate în primul cadran (și parțial, în al doilea); derivatele respective ne permit să determinăm curbura în fiecare punct (cu unele excepții) și să figurăm (parțial și nu tocmai corect, fiindcă deocamdată vizăm numai porțiunea din primul cadran) evoluta lui $\boldsymbol{\mathfrak{D}}$ — locul centrelor cercurilor de curbură (care de regulă, ne-ar releva câte ceva despre proprietățile curbei respective…).
Nu-i cazul să redăm în LaTeX calculele sau formulele respective, fiindcă oricine le poate face (folosind eventual, SageMath); reproducem totuși, ca imagine, foaia finală a calculului nostru — cu această precizare: în formulele inițiale (4), am renotat $t^2$ cu $t$:

Intuitiv, punctul în care curbura este cea mai mică este $D$ (deci pentru $t=\frac{\sqrt{3}-1}{2}\approx 0.366$); în figura următoare am reprezentat (cu albastru) cercurile osculatoare corespunzătoare punctelor $D$ și $B$ (cu centrele marcate roșu):

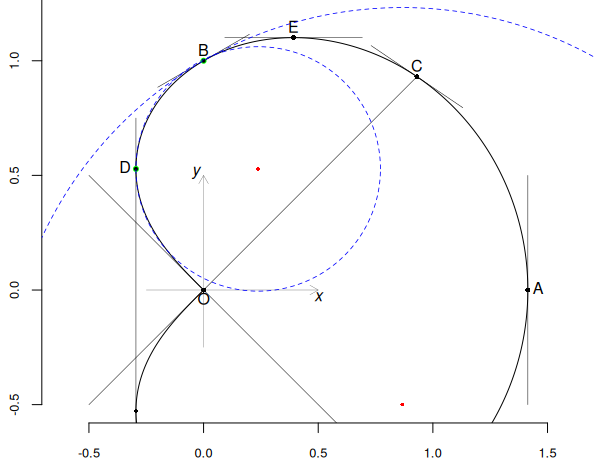
Precizăm că raza cercului osculator în punctul $(x(t),\,y(t))$ este dată de $R(t)$, iar centrul (aflat pe normala punctului respectiv) are coordonatele $(\alpha(t),\,\beta(t))$ din foaia de calcul redată mai sus. Pe figura următoare am redat cercurile osculatoare pentru $t\in(0,\,0.1]$ (cu pasul 0.005); centrele lor (punctele "roșu") formează o primă imagine interesantă (punctele marcate cu verde sunt cele cărora le sunt asociate cercurile trasate:):

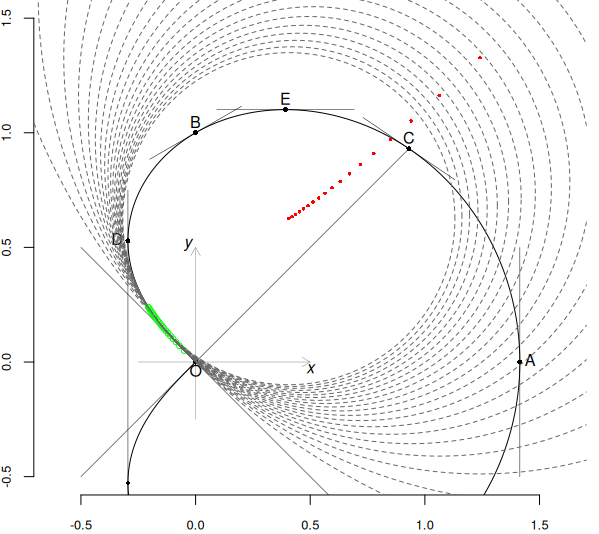
În sfârșit, figura următoare vizează $t\in(0,\,\boldsymbol{\sqrt[3]{3}\,})$; până la $t=\boldsymbol{\sqrt[3]{3}}$, curbura (= $1/R(t)$) este negativă, iar centrele cercurilor osculatoare se află pe porțiunea spre interior a normalelor, cum se vede pe figură; în schimb, pentru $t\gt \boldsymbol{\sqrt[3]{3}}$ (când curbura devine pozitivă), direcția în care se află centrele de curbură se inversează (nu mai redăm aici, situația respectivă, mai ales că intuitiv… parcă este pe dos de cum ar trebui):

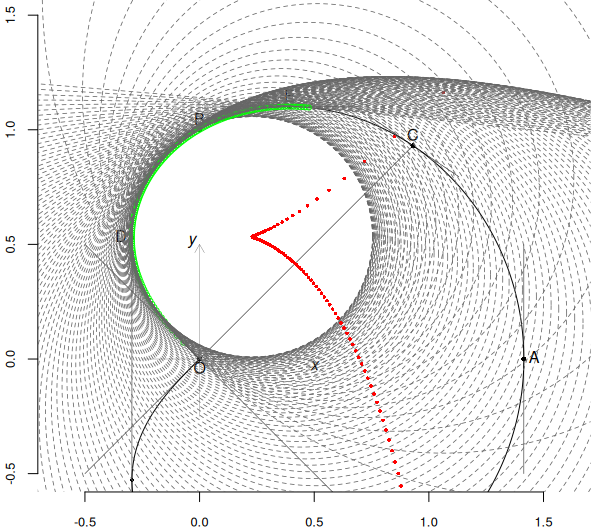
Locul centrelor de curbură pare a fi o tractrice, sau așa ceva… Dar nu putem trage nicio concluzie, tocmai fiindcă n-am reușit să considerăm întreaga curbă $\boldsymbol{\mathfrak{D}}$ (ci doar "un cadran" al ei). Nici ecuația polară (2) și nici ecuațiile parametrice (4) nu pot genera în întregime curba (ci doar "pe cadrane", schimbând $\theta$ în $(\theta + \pi)$, respectiv schimbând semnele coordonatelor); numai ecuația implicită (3) ar putea să genereze "deodată" întreaga curbă (dar numai dispunând de contourLines(), adică văzând curba ca secțiune plană, la cota 0, a unei anumite suprafețe) și rămâne de văzut dacă adaptând calculele de mai sus pentru (3), vom putea să trasăm corect evoluta lui $\boldsymbol{\mathfrak{D}}$ (folosind contourLines() pentru a plota centrele cercurilor de curbură).