Alipind un bit $\varepsilon$ formei binare a unui număr care are restul $h$ față de $M$, obținem forma binară a unui număr cu restul $k=2h+\varepsilon\,\,(\mathrm{mod}\,M)$; pentru oricare multiplu de $M$, forma binară a sa rezultă concatenând biții de pe arcele unuia dintre ciclurile care pleacă din starea $0$ a automatului rezultat.
Problema pusă în [1], de a caracteriza printr-o expresie regulată, formele binare ale multiplilor de $(M+h)$, revine la a îmbina cumva, "pe porțiuni", anumite cicluri care pleacă din starea $h$ (pentru $0\le h\lt M$).

Trebuie să ne bazăm pe anumite cicluri, nu pe toate ? pe cicluri, sau doar pe circuite ?

Pentru $M$ mic, de exemplu $M=7$, structura ciclurilor este ușor de investigat direct:

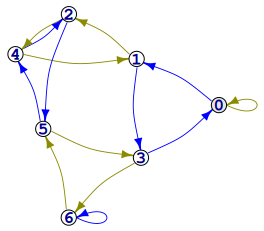
Vedem imediat ciclurile simple $(C_1): 0-1-3-0$ și $(C_2): 1-2-4-1$, din care deducem prin conjugare (v. [1]) — sau vedem și direct — ciclurile $(C_3): 6-5-3-6$ și $(C_4): 5-4-2-5$; să considerăm și "arcul dublu" (auto-conjugat) $(C_5): 2-4-2$.
Să observăm că împreună, aceste 5 cicluri acoperă graful: exceptând buclele $0-0$ și $6-6$, oricare arc este conținut în unul sau altul dintre ciclurile respective. Deci, în principiu, oricare alt ciclu (elementar sau nu) s-ar putea exprima ca o "combinație" a unora dintre aceste 5 cicluri simple…. Modalitatea de combinare este sugerată de modul evident prin care dintr-un ciclu ne-elementar, rezultă un ciclu elementar pe aceleași noduri: eliminăm arcele care apar de două sau mai multe ori.

Pentru un exemplu simplu, ciclul $(Q):5-4-1-2-5$ se obține din $(C2)$, $(C4)$ și $(C5)$ ca diferența simetrică (sau "reuniunea disjunctă") a mulțimilor de arce ale acestora (excluzând arcele $2-4$ și $4-2$, prin care trec câte două dintre aceste trei cicluri).

Însă ciclul $4-1-3-6-5-4$ nu poate fi obținut pe baza celor 5 cicluri: reuniunea disjunctă a mulțimilor de arce ale acestora conține într-adevăr, arcele ciclului menționat — dar conține și arcele $0-1$, $3-0$, $1-2$ și $2-5$, care nu pot fi excluse decât considerând și ciclul $(C6): 0-1-2-5-3-0$ (și tot nu-i sigur că sunt suficiente aceste 6 cicluri, pentru a exprima oricare alt ciclu).
Prin urmare, nu ajunge să "vedem imediat"… Avem nevoie de o metodă sigură, prin care să construim o "bază de cicluri" (care să genereze toate ciclurile).

Mai sus, am generat un nou ciclu $(Q)$ combinând prin "reuniune disjunctă" mulțimile de arce ale unor cicluri "de bază" — dar ce înseamnă aceasta, mai precis ?

Citind biții de pe arcele consecutive ale ciclului (precizăm că arcele colorate blue reprezintă biți '1'), avem secvențele binare '000' pentru $(C2)$, respectiv '111' pentru $(C4)$ și '01' pentru $(C5)$ — cu semnificația asumată la început (v. [1]): alipind secvența de biți respectivă, cuvântului binar existent în starea din care pleacă ciclul respectiv, obținem un nou cuvânt binar, reprezentând un număr congruent $(\mathrm{mod}\,M)$ celui reprezentat în starea din care a plecat ciclul.

Dar dacă este vorba nu de trecere (prin "alipire") într-o altă stare, ci de generarea unui alt ciclu — atunci avem nevoie (evident) nu numai de secvența de biți citită de pe arcele fiecăruia dintre ciclurile "de bază", dar și de arcele acestora… Putem ține seama și de acest aspect, indexând biții citiți de pe arcele ciclurilor, prin arcele grafului (constituind matricea de incidență a ciclurilor):

                 edges (fără buclele '00' și '66')
    cycles        12 24 36 41 53 65 01 13 25 30 42 54   Biții arcelor
      C2: 1-2-4-1  1  1  0  1  0  0  0  0  0  0  0  0   '000'
      C4: 5-4-2-5  0  0  0  0  0  0  0  0  1  0  1  1   '111'
      C5: 2-4-2    0  1  0  0  0  0  0  0  0  0  1  0   '01'

O operație xor() între liniile acestei matrice ne dă vectorul:

   12    24    36    41    53    65    01    13    25    30    42    54
 TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE

care are valoarea TRUE numai pe acele arce care apar într-unul singur, dintre cele trei cicluri — deci vectorul respectiv indică arcele ciclului $(Q): 5-4-1-2-5$, obținut mai sus (direct) ca "reuniunea disjunctă" a ciclurilor (de sesizat încă o "problemă" care poate apărea: nu totdeauna, rezultatul formează un ciclu…).
În matricea redată mai sus, am boldat valorile '1' corespunzătoare arcelor blue — încât vedem direct din matrice, secvența binară a lui $Q$: '1001' (de valoare 9). Numărul reprezentat în starea $5$ din care pleacă ciclul $Q$ este de forma $7q+5$; alipind formei binare a acestuia, secvența '1001', rezultatul va reprezenta numărul $2(7q+5)+9$, care se vede imediat că are tot restul $5$ (față de $7$).

În sfârșit, să observăm că dacă am combina (prin xor) ciclurile $1-2-5-3-1$ și $4-2-5-4$ (ceea ce revine la a exclude arcul comun $2-5$), am obține "ciclul" $1-2-\boldsymbol{4-5}-3-1$ care… este un ciclu doar ca graf neorientat (arcul real este $5-4$, nu $4-5$). Deci trebuie să distingem între categorii de cicluri; de obicei, se folosesc termenii ciclu pentru grafuri neorientate și circuit, pentru cele orientate.
Dar cum să interpretăm biții corespunzători unui "ciclu" în care apare un arc de sens contrar celui real (mai putem "alipi" cumva, secvența de biți respectivă) ??

În concluzie:

Poate că pentru $M$ mic, am putea proceda și empiric (ca în încercarea de mai sus); totuși trebuie să apelăm la o metodă sigură, pentru a obține o "bază de cicluri". De fapt, putem găsi mai multe asemenea baze, între care eventual să alegem; ne-ar conveni o bază minimală, în care numărul total de arce să fie cât mai mic și desigur, ne-ar conveni o bază formată numai din circuite (fără "semi-cicluri", în care un arc are orientare contrară celei reale).

Pentru a permite "alipirea" secvențelor de biți, avem de generat circuite și nu cicluri (neorientate); cu siguranță, pentru generarea circuitelor avem de folosit matricea de incidență a ciclurilor de bază și operații xor între liniile acesteia.

Pentru grafuri, noi folosim rigraph, sau networkx; aceste pachete oferă și funcții care determină o "bază de cicluri", dar (deocamdată) numai pentru grafuri neorientate (nu și pentru digrafuri… Se știe însă, că un digraf care este tare-conex — cum avem în cazul automatului mod $M$ — admite o bază de circuite; dar algoritmul care ar găsi-o este sofisticat și pare foarte complicat de implementat).