Transformarea fișierului PGN în obiect de date (II)
Asupra unei colecții de partide proprii
vlbz este ceva jucător de șah, nelegitimat la vreun club profesionist, dar înregistrat pe lichess.org – de unde am descărcat fișierul lichess_vlbz_2023-04-02.pgn, conținând partidele sale de „șah rapid” (cu limita individuală de 15 minute) din ultimii vreo doi ani.
Fișierul PGN menționat nu conține caractere '\r', iar mutările fiecărei partide (inclusiv uneori, adnotări) sunt înregistrate pe câte o singură linie de text – încât îi putem aplica direct pgn_dfr() din [1], obținând un data.frame cu 2569 linii (partide) pe 21 de coloane:
# stats.R (statistici pe o colecție PGN de la Lichess) library(tidyverse) WB <- readRDS("lichess_vlbz.RDS") # 2569 obs. (partide) pe 21 variabile > colnames(WB) # "WB" ar veni de la White/Black... [1] "Event" "Site" "Date" "White" [5] "Black" "Result" "UTCDate" "UTCTime" [9] "WhiteElo" "BlackElo" "WhiteRatingDiff" "BlackRatingDiff" [13] "Variant" "TimeControl" "ECO" "Opening" [17] "Termination" "Annotator" "moves" "BlackTitle" [21] "WhiteTitle"
Cel mai important tag este Site (care conține de exemplu "https://lichess.org/UuQMWXtf"); pastând conținutul în bara de adresă a unui browser, putem vizualiza desfășurarea partidei respective și avem posibilitatea de a analiza mutările folosind Stockfish:
Unele tag-uri apar doar în câteva partide; map_dfr() (v. [1]) le-a montat abia când a dat de ele, deci după coloana $moves. Nu este necesar, totuși relocăm $moves pe ultimul loc:
> WB <- WB %>% relocate(., moves, .after = last_col())
În WB toate coloanele au tipul chr, dar trebuie să avem în vedere (pentru calcule) că unele semnifică fie date calendaristice (într-un anumit format inițial), fie valori numerice:
> WB <- WB %>% mutate(Date = as.Date(Date, format="%Y.%m.%d"), UTCDate = as.Date(UTCDate, format="%Y.%m.%d"), WhiteElo = as.integer(WhiteElo), BlackElo = as.integer(BlackElo), WhiteRatingDiff = as.integer(WhiteRatingDiff), BlackRatingDiff = as.integer(BlackRatingDiff)) > saveRDS(WB, "lichess_vlbz.RDS") # salvăm modificările
Sistemul Elo, folosit în multe sporturi, măsoară performanța fiecărui jucător după rezultatele curente ale sale, în confruntările avute cu ceilalți. La înregistrare pe Lichess, ți se atribuie un coeficient Elo inițial (parcă 1500); apoi, pe măsură ce joci, coeficientul se modifică mai mult sau mai puțin, în funcție de rezultate și de coeficienții celor cu care ai jucat.
În principiu, ți se repartizează aleatoriu un nou partener – dar cel mai probabil, cu un coeficient Elo care nu este prea depărtat de cel propriu (actual).
Să vedem câte ceva despre coeficienții partenerilor lui vlbz:
bl2 <- WB %>% filter(White == "vlbz") %>% pull(BlackElo) wh2 <- WB %>% filter(Black == "vlbz") %>% pull(WhiteElo) Elo2 <- c(bl2, wh2) # coeficienții partenerilor lui 'vlbz' cdf2 <- ecdf(Elo2) # distribuția cumulativă empirică plot(cdf2, cex=0.4, main = "ELO parteneri - distribuția cumulativă", xlab = "x = coeficient ELO"); grid() print(summary(cdf2)) #Empirical CDF: 518 unique values with summary # Min. 1st Qu. Median Mean 3rd Qu. Max. # 1431 2031 2162 2157 2291 2604 curve(pnorm(x, mean(Elo2), sd(Elo2)), # adăugăm distribuția cumulativă teoretică from = min(Elo2), to = max(Elo2), add = TRUE, col='red', lwd = 1.5)
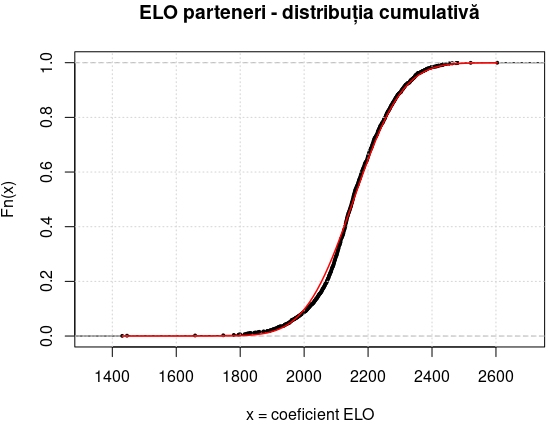
Graficul arată că distribuția coeficienților partenerilor este foarte apropiată de cea normală (pe aceeași medie și abatere standard ca a coeficienților existenți) – ceea ce confirmă prezumpția că următorul partener ce-ți va fi alocat aleatoriu, are un coeficient Elo nu prea depărtat, de media celor cu care ai jucat până în momentul respectiv (dar luând în considerație și variația curentă a coeficientului propriu).
De pe grafic citim că dintre parteneri, vreo 60% au coeficienți sub 2200 și aproape 40%, au calificare mai înaltă (de regulă, 2200-2300 corespunde teoretic categoriei „candidat de maestru”; de la 2300 în sus avem „maeștri” și „mari maeștri”); valorile obținute prin summary() (redate mai sus) ne arată că 25% dintre partenerii lui vlbz aveau Elo între 2157 și 2291.
Ne-ar interesa acum, variația în timp a coeficientului Elo al lui vlbz.
Trebuie să avem în vedere nu numai data calendaristică, dar și momentul de timp al inițierii partidei (indicat de UTCTime) – fiindcă vlbz a putut juca mai multe partide într-o aceeași zi.
Observăm întâi că $Date și $UTCDate conțin aceleași valori (vor diferi probabil, pentru altă categorie decât "Rapid" – de exemplu pentru "correspondence"):
> identical(WB$Date, WB$UTCDate) # [1] TRUE
Deci nu vom avea nevoie de UTCDate; îmbinăm (prin stringr::str_glue()) valorile $UTCDate (de tip date) și $UTCTime (de tip time), într-o nouă coloană $DateTime – pe care o aducem prin lubridate::ymd_hms(), la tipul date-time; apoi, ordonăm liniile după valorile $DateTime:
> WB <- WB %>% mutate(DateTime = str_glue("{UTCDate} {UTCTime}") %>% lubridate::ymd_hms()) %>% mutate(UTCDate = NULL, UTCTime = NULL) %>% arrange(DateTime) > saveRDS(WB, "lichess_vlbz.RDS") # salvăm, pentru orice eventualitate
Selectăm WhiteElo sau BlackElo, după cum vlbz a jucat cu albul, respectiv cu negrul (și reunim datele prin full_join()); plotăm variația coeficientului Elo al lui vlbz, începând din a doua parte a anului 2020:
Wh <- WB %>% filter(White == 'vlbz') %>% select(DateTime, WhiteElo) Bl <- WB %>% filter(Black == 'vlbz') %>% select(DateTime, BlackElo) vlbz_elo <- full_join(Wh, Bl) %>% mutate(Elo = ifelse(is.na(WhiteElo), BlackElo, WhiteElo)) %>% select(DateTime, Elo) %>% arrange(DateTime) from <- lubridate::ymd_hms("2020-07-01-00-00-00") plot(vlbz_elo %>% filter(DateTime > from), type = "l", ylab="coeficient Elo (Glicko2)"); grid()
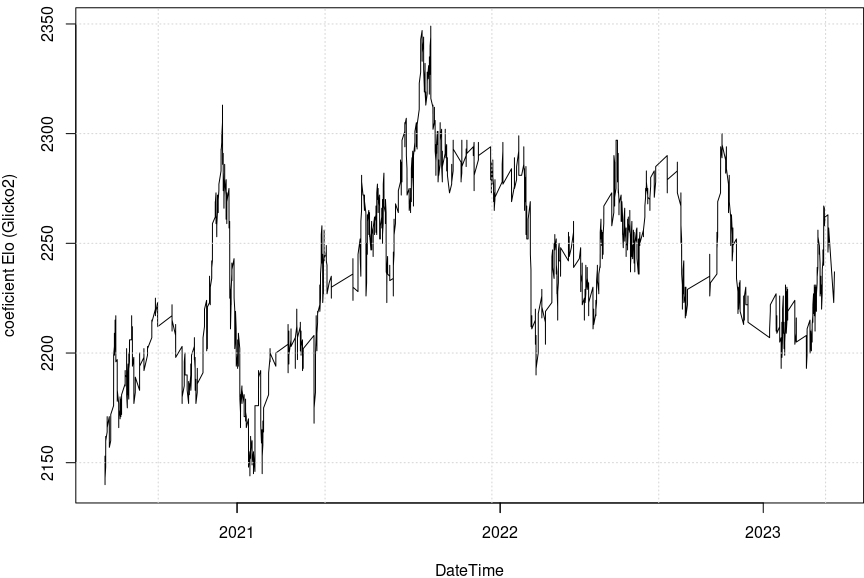
Tag-urile WhiteRatingDiff și BlackRatingDiff înregistrează valorile cu care cresc sau scad coeficienții Elo ai celor doi jucători, la încheierea partidei respective; cum se vede pe grafic, aceste valori pot să fie și foarte mari – ceea ce pare totuși ciudat…
Între timp, am aflat că de fapt se folosește nu sistemul Elo obișnuit, ci unul mai elaborat (v. Glicko-2); pentru fiecare coeficient se calculează un „interval de încredere”, asigurând că în 95% dintre cazuri, coeficienții sunt în intervalul [500, 2500].
În principiu, câștigul la unul care are Elo foarte mare față de al tău, va mări sensibil coeficientul Elo propriu (la început, când ai 1500 – chiar și cu câteva sute de puncte; pe măsură ce joci mai multe partide și lucrurile se stabilizează, creșterea devine totuși de ordinul unei zeci de puncte); la fel, pierderea la un jucător mult mai slab cotat diminuează chiar foarte abrupt (de ordinul a 30 puncte), coeficientul Elo propriu.
Pentru o imagine similară celeia redate mai sus, totuși mai „netedă” – să considerăm medile pe fiecare lună, ale coeficienților Elo proprii.
Ignorăm liniile cu Elo mai mic decât 2100, fiindcă în prima lună, decembrie 2019, vlbz a crescut abrupt de la 1500 până pe la 2100 și ulterior (cum se vede pe imaginea de mai sus), n-a mai coborât sub 2100.
Din valorile $DateTime reținem într-o nouă coloană $YM anul și luna (având grijă să formatăm numărul lunii pe câte două poziții, prin str_pad() – pentru a avea ordinea firească a lunilor). Apoi, grupăm datele după valorile din coloana YM și calculăm prin summarize(), media Elo corespunzătoare fiecărui grup:
library(lubridate) VZE <- vlbz_elo %>% filter(Elo > 2100) %>% mutate(YM = paste(year(DateTime) %% 100, # ultimele 2 cifre ale anului str_pad(month(DateTime), 2, side="left", pad="0"), sep = "-")) %>% group_by(YM) %>% summarize(avgElo = round(mean(Elo))) # > head(VZE, 4) # # A tibble: 4 × 2 # YM avgElo # 1 20-01 2206 # media Elo pe ianuarie 2020 # 2 20-02 2217 # 3 20-03 2251 # 4 20-04 2147
Putem afișa rezultatele ca atare, cum am exemplificat aici prin head(), dar preferabil este să le plotăm; folosim de data aceasta pachetul ggplot2 (inclus în tidyverse):
G <- ggplot(VZE, aes(x = YM, y = avgElo, group = 1)) + geom_line(colour = "steelblue") + labs(x = "An-Lună", y = "medie Elo") + ggtitle("Valorile medii lunare ale coeficientului Elo al 'vlbz'") + theme(axis.text.x = element_text(angle = 90, vjust = 0.5, hjust=1)) plot(G)
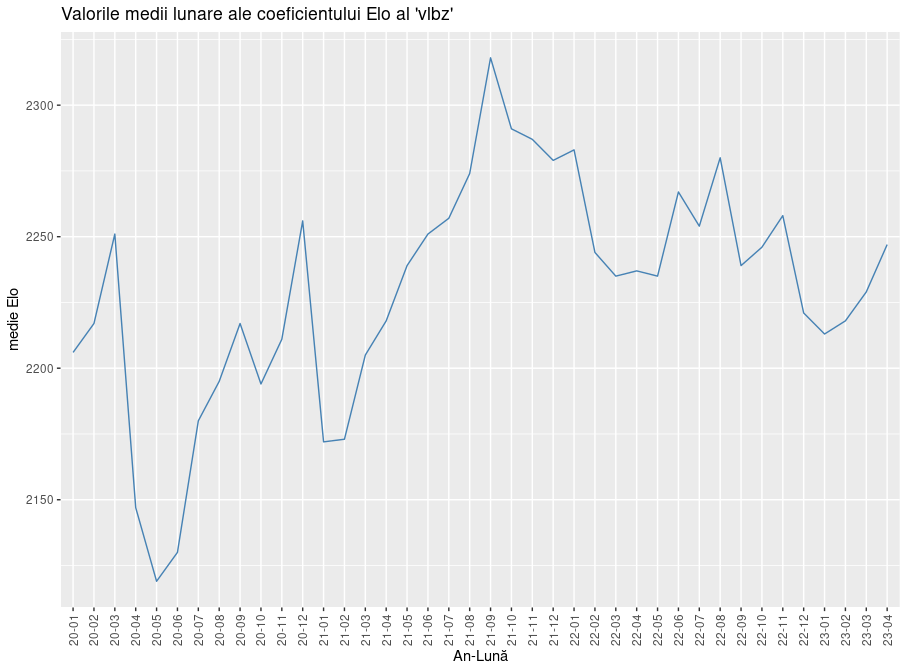
Se vede pe grafic că vlbz a depășit 2300, vreme de vreo două săptămâni, după care a început să se mențină în jurul cotei 2250.
Să vedem și rezultatele (partide câștigate / pierdute / remiză), pe categorii de parteneri – să zicem, din sută în sută pentru Elo de la 2000 la 2300:
VZ2 <- WB %>% mutate(Elo2 = if_else(White == "vlbz", BlackElo, WhiteElo), Cat2 = case_when(Elo2 < 2000 ~ "..2000", Elo2 < 2100 ~ "..2100", Elo2 < 2200 ~ "..2200", Elo2 < 2300 ~ "..2300", TRUE ~ "> 2300"), Res = case_when(White == "vlbz" & Result == "1-0" ~ "+", Black == "vlbz" & Result == "0-1" ~ "+", Result == "1/2-1/2" ~ "=", TRUE ~ "-")) %>% select(Cat2, Res) fr <- addmargins(table(VZ2)) # frecvența rezultatelor, pe categorii de Elo Res Cat2 - + = Sum # Pierdute(-) Câștigate(+) Remiză(=) ..2000 27 136 8 171 ..2100 152 328 22 502 ..2200 354 532 75 961 ..2300 300 275 60 635 > 2300 168 95 37 300 Sum 1001 1366 202 2569
sau procentual, față de totalurile Sum (pe orizontală, iar în ultima coloană pe verticală):
fr1 <- round(fr[,1:3] / fr[,4], 2) fr2 <- cbind(fr1, round(fr[, 4] / fr[6,4], 2)) > fr2 <- fr2 * 100 # valori procentuale - + = ..2000 16 80 5 7 ..2100 30 65 4 20 ..2200 37 55 8 37 ..2300 47 43 9 25 > 2300 56 32 12 12 Sum 39 53 8 100
Cei mai mulți dintre partenerii alocați aleatoriu lui vlbz, anume 37%, au Elo între 2100 și 2200 iar rezultatele partidelor respective sunt +55% -37% =8%.
Pentru cele 25% partide cu jucători 2200-2300, rezultatele sunt echilibrate: +43% -47% =9%; iar în cazul celor 12% partide cu jucători peste 2300, rezultatele sunt probabil onorabile: +32% -56% =12%.
Iar pentru totalul de 2569 partide: +53% -39% =8%.
Prin mosaicplot() putem reda și grafic, tabelul de contingență rezultat mai sus prin table():
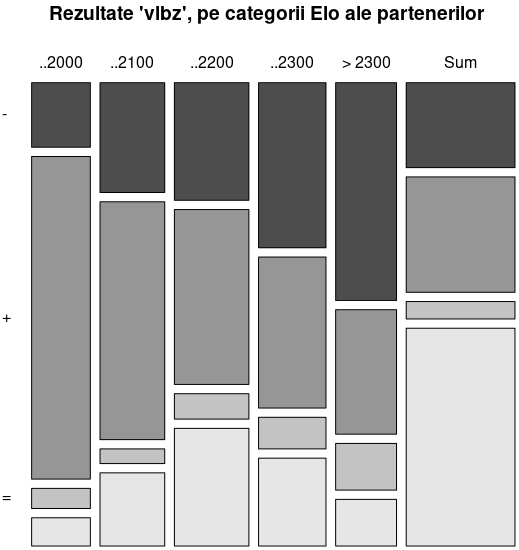
Avem mai sus, exprimări tipice și posibilități de a le obține folosind R, pentru statisticile care ne-au interesat imediat (asupra Elo-urilor partenerilor unui jucător dat, asupra variației în timp a coeficientului Elo al jucătorului și desigur, asupra rezultatelor sale).
Dar între timp, am descoperit că Lichess deja furnizează prin link-ul Chess Insights (după ce intri pe contul propriu și accesezi Profile) o gamă foarte largă de statistici, asupra colecției curente de partide proprii… Memorabilă ca idee este statistica pe numărul de mutări de pion, de cal, de rege, etc. efectuate în partidele respective, împreună cu câte o apreciere a acurateței acestora (bazată pe evaluările furnizate „în spate” de Stockfish).
Mai mult, putem dispune de o specificație de programare OpenAPI și deasemenea, putem accesa openDataBase; de exemplu, pentru „statistici de performanță” am avea de formulat cereri ca GET /api/user/{username}/perf/{perf}.
Lichess și Stockfish (ambele, de tip "open-source") sunt cel mai impresionante și instructive aplicații de șah, de care putem dispune – și nu numai pentru a practica șahul, dar și pentru a învăța șah și a urmări evenimentele șahiste majore; deasemenea, pentru a studia statistică matematică (pe seturi de date reale), sau "computer-chess" și chiar, pentru a exersa de exemplu (ca și în studiul de față) programarea în limbajul R.
vezi Cărţile mele (de programare)