1. Reţele de puncte

Presupunem fie un segment indicat prin afixul mijlocului, lungime şi direcţie (vector director), fie un pătrat cu laturile paralele axelor, indicat prin afixul centrului şi lungimea laturii; prin funcţia următoare, construim o reţea de puncte echidistanţate cu un anumit pas, aparţinând segmentului sau pătratului respectiv - dar avem în vedere şi cazul când este indicat un vector conţinând mai multe afixe (de mijloace de segmente, respectiv de centre de pătrate):

make_grid <- function(center, length,  npoints=100, director=NULL) {
  l2 <- length / 2  # distanţa centrului faţă de latură (sau capăt)
  Z <- as.complex()
  if(is.null(director))  {  # pătrate (cu laturile paralele axelor)
    for(cg in center) {
      x <- seq(from=Re(cg)-l2, to=Re(cg)+l2, len=npoints)
      y <- seq(from=Im(cg)-l2, to=Im(cg)+l2, len=npoints)
      mesh <- expand.grid(x, y)
      Z <- append(Z, mesh$Var1 + 1i*mesh$Var2)
    }
    return(Z)
  }
  if(Arg(director) == 0) {  # segmente orizontale
    for(cg in center)
      Z <- append(Z, seq(from=Re(cg)-l2, to=Re(cg)+l2, len=npoints)
                     + 1i*Im(cg))
    return(Z)
  }
  if(Arg(director) == pi / 2) {  # segmente verticale
    for(cg in center)
      Z <- append(Z, Re(cg) + 
                     1i*seq(from=Im(cg)-l2, to=Im(cg)+l2, len=npoints))
    return(Z)
  }
  for(cg in center) {  # segmente paralele vectorului director
    s <- l2 / Mod(director)
    dx <- Re(director); dy <- Im(director)
    Z <- append(Z, seq(from=Re(cg)-s*dx, to=Re(cg)+s*dx, len=npoints)
                   + 1i*seq(from=Im(cg)-s*dy, to=Im(cg)+s*dy, len=npoints))
  }
  return(Z)
}

În secvenţa (şi figura) următoare ilustrăm (parţial) posibilităţile funcţiei de mai sus:

mesh <- make_grid(c(1, 2+1i), 4, np=40)  # două pătrate
plot(mesh, asp=1)
points(c(make_grid(c(-0.5+2.5i, 3.5-1.5i), 2, dir=1+1i),
         make_grid(1.5+0.5i, 6, dir=1-1i)), 
       cex=0.3, pch=19)  # set de segmente oblice
lines(c(make_grid(1, 4, dir=0),  # segment orizontal 
        make_grid(2+1i, 4, dir=1i)))  # segment vertical

În treacăt, precizăm că make_grid() înlocuieşte funcţia "mai slabă" build_mesh() din [1] (aceasta cerea coordonate de colţuri opuse, viza numai segmente verticale sau orizontale şi asuma un pas liniar al reţelei de puncte).

Fiindcă în toate cele patru cazuri disociate în make_grid() am implicat funcţia seq(), să precizăm şi aici că seq(from, to, len) produce "reţeaua" de len valori echidistante cuprinse între from şi to; de exemplu în primul caz (pătrat cu laturile paralele axelor), am determinat reţelele 'x' şi 'y' pentru două laturi alăturate, apoi am făcut produsul cartezian al lor (folosind expand.grid(), care pune valorile lui 'x' şi respectiv 'y' - împerecheate în toate modurile - în coloanele "Var1" şi "Var2") şi am format vectorul complex x + i y (pe care l-am adăugat prin append() în vectorul complex 'Z' - returnat în final ca fiind reţeua de puncte asociată tuturor pătratelor ale căror centre au fost indicate în parametrul 'center').

Pentru ultimul caz ("segmente paralele vectorului director") avem această acoperire matematică: punctele dreptei care trece prin punctul de afix z₀ = 'cg' şi are vectorul director dat prin numărul complex V (încât panta dreptei este Im(V) / Re(V), pentru Re(V) ≠ 0) au afixele z = z₀ + s V, cu s ∈ R; punctele z₁ = z₀ + s V şi z₂ = z₀ - s V de pe această dreaptă sunt simetrice faţă de punctul z₀ şi din condiţia ca lungimea segmentului z₁z₂ să fie egală cu valoarea din parametrul 'length' rezultă că s = λ / Mod(V) unde λ este 'length' / 2 (iar funcţia Mod() ne dă modulul unui număr complex).

2. Transformarea punctelor prin exponenţiala complexă

Tastând = exp(1 + i) în bara de căutare a browserului ("Google Search"), se obţine răspunsul "exp(1 + i) = 1.46869394 + 2.28735529 i" şi acest experiment foarte obişnuit poate părea suficient pentru o primă explicaţie asupra funcţiei de variabilă complexă exp()… Ceva matematică suplimentară este desigur de dorit şi este chiar mai accesibilă, decât o chestiune "de programare" care poate părea mai firească: oare cum este implementată exp()? (nu cum s-ar crede, ca serie de puteri (Taylor), ci - mai precis în privinţa erorilor de rotunjire şi mai rapid - utilizând anumite "trucuri" de calcul şi un set de "instrucţiuni speciale" specifice microprocesorului).

Următorul program cu caracter experimental (lung, fiindcă am tratat fiecare caz în parte - vezi secţiunile marcate prin câte o linie de comentariu) ilustrează transformarea dreptelor (orizontale, verticale, sau oblice) prin funcţia de variabilă complexă exp():

require(RColorBrewer)  # Creates nice looking color palettes
col8 <- brewer.pal(8, "Set3")  # "Paired"
# stabilim limitele axelor şi "aspect-ratio", apoi mărimea şi forma punctelor
plot(-pi, pi, type="n", xlim=c(-pi, pi), ylim=c(-pi,pi), asp=1)  # [-π, π] × [-π, π]
opar <- par(cex=0.3, pch=19, mar=c(1,1,1,0))
# reţele de puncte pentru drepte orizontale
mesh_h1 <- make_grid(2i, 2*pi-0.1, d=0)
mesh_h2 <- make_grid(-2i, 2*pi-0.1, d=0)
points(mesh_h1, col=col8[1])  # plotează dreptele
points(mesh_h2, col=col8[2])
points(exp(mesh_h1), col=col8[1])  # plotează transformatele dreptelor
points(exp(mesh_h2), col=col8[2])
# reţele de puncte pentru drepte verticale (şi plotări)
mesh_v1 <- make_grid(1, 2*pi-0.1, d=1i)
mesh_v2 <- make_grid(-1, 2*pi-0.1, d=1i)
points(mesh_v1, col=ifelse(Im(mesh_v1)>0, col8[3], col8[4]))
points(mesh_v2, col=ifelse(Im(mesh_v1)>0, col8[5], col8[6]))
points(exp(mesh_v1), col=ifelse(Im(mesh_v1)>0, col8[3], col8[4]))
points(exp(mesh_v2), col=ifelse(Im(mesh_v1)>0, col8[5], col8[6]))
# trasează şi etichetează vectori 'z' şi 'exp(z)', pentru o dreaptă verticală
arrows(0,0,Re(mesh_v1[70]), Im(mesh_v1[70]), lwd=0.9, col=col8[4], len=0.1)
arrows(0,0,Re(exp(mesh_v1[70])), Im(exp(mesh_v1[70])), lwd=0.9, col=col8[4], len=0.1) 
arrows(0,0,Re(mesh_v1[130]), Im(mesh_v1[130]), lwd=0.9, col=col8[3], len=0.1)
arrows(0,0,Re(exp(mesh_v1[130])), Im(exp(mesh_v1[130])), lwd=0.9, col=col8[3], len=0.1) 
text(mesh_v1[70], labels="z1", pos=4, cex=3, col=col8[4])
text(exp(mesh_v1[70])+0.03-0.03i, labels="exp(z1)", pos=4, cex=3, col=col8[4], srt=-30)
text(mesh_v1[130], labels="z2", pos=4, cex=3, col=col8[3])
text(exp(mesh_v1[130])+0.05+0.05i, labels="exp(z2)", pos=4, cex=3, col=col8[3], srt=30)
# reţea de puncte pe o dreaptă oblică; plotare şi marcare de vectori şi transformate
mesh_o <- make_grid(-0.5+0.5i, 2*pi, d=cos(pi/3)+1i*sin(pi/3))
points(mesh_o, col="black", cex=0.2)
points(exp(mesh_o), col="black", cex=0.2)
arrows(0,0,Re(mesh_o[170]), Im(mesh_o[170]), lwd=0.9, col="black", len=0.1)
arrows(0,0,Re(exp(mesh_o[170])), Im(exp(mesh_o[170])), lwd=0.9, col="black", len=0.1) 
text(mesh_o[170]+0.03+0.05i, labels="z3", pos=2, cex=3, col="black")
text(exp(mesh_o[170])-0.5, labels="exp(z3)", pos=4, cex=3, col="black", srt=15)
# marchează puncte pe dreptele orizontale şi transformatele lor
points(mesh_h1[110], col=col8[1], cex=3, pch=15)
points(exp(mesh_h1[110]), col=col8[1], cex=3, pch=15)
points(mesh_h2[110], col=col8[2], cex=3, pch=15)
points(exp(mesh_h2[110]), col=col8[2], cex=3, pch=15)
# reconstituie parametrii grafici iniţiali şi adaugă un titlu
par(opar)
title(main="transformarea dreptelor prin exponenţiala complexă", 
      cex.main=1, font.main=3, col.main="sienna4")

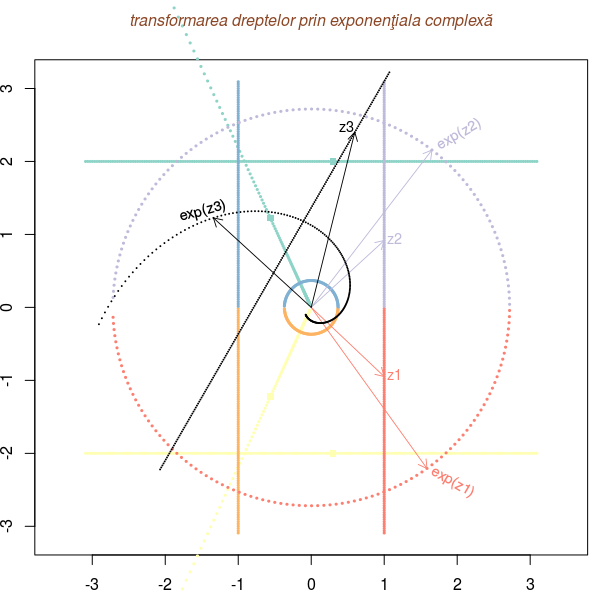
Am trasat două "drepte" orizontale (la ordonatele 2 şi -2), două drepte verticale (de abscise 1 şi -1, colorând diferit semidreptele separate de axa reală) şi o dreaptă oblică; am marcat şi am etichetat unele puncte z şi transformatele acestora, exp(z).

Corelând culorile dreptelor (şi semidreptelor) cu ale transformatelor acestora, am deduce că o dreaptă orizontală este transformată într-o rază care pleacă din originea sistemului de axe; o dreaptă verticală este transformată într-un cerc cu centrul în origine (semicercurile separate de axa reală corespunzând semidreptelor); iar o dreaptă oblică devine o spirală în jurul originii.

Ca să nu încarc mai mult figura (şi programul redat mai sus), am omis să evidenţiez cum se transformă axa reală şi axa imaginară… Ne străduim acum să argumentăm cât mai simplu (şi eventual, să corectăm), cele deduse vizual mai sus.

Dacă z = x + i y atunci e^z = e^x e^i y = e^x (cos y + i sin y); deci abscisa x a punctului iniţial determină (în mod unic) modulul e^x al transformatului (sau, lungimea vectorului de poziţie al acestuia), iar ordonata y (dar şi y + 2kπ, k ∈ Z) determină argumentul (unghiul polar) al acestuia. Punctul z' = x + i (y + 2kπ) are aceeaşi imagine ca şi punctul z (având cos(y + 2kπ) = cos  y şi la fel pentru sin()); altfel spus, două puncte de o aceeaşi abscisă, distanţate vertical cu 2kπ (k ∈ Z) au o aceeaşi imagine (sau formulând pedant: e^z este funcţie periodică, de perioadă imaginară 2kπ i).

e^z nu poate lua valoarea 0 (fiindcă | e^z | = e^x ≠ 0), dar poate avea ca valoare orice număr complex nenul (determinând x pentru care e^x egalează lungimea vectorului de poziţie a punctului dat şi luând ca y unghiul polar al acestui vector). Ţinând cont de periodicitatea "pe verticală" evidenţiată mai sus, pare suficient să studiem e^z doar pentru punctele z conţinute în banda orizontală delimitată de dreptele y = -π şi y = π (cum am şi procedat în programul de mai sus); pentru punctele acestei benzi, e^z ia toate valorile complexe nenule, în mod biunivoc.

Desigur, în banda orizontală considerată nu avem "drepte" verticale, ci doar segmente; dacă z descrie un segment vertical fixat, z = a + i y (cu a=constant şi y ∈ (-π, π]), atunci e^z = e^a e^i y descrie "unu-la-unu" un cerc de rază e^a centrat în origine; în particular, pentru a = 0, găsim că imaginea segmentului vertical de pe axa imaginară este cercul unitar (cel de rază 1, centrat în origine). Să observăm că pentru punctele z' ale prelungirii în banda superioară (π, 3π] a segmentului considerat, avem ca imagine (a doua oară) acelaşi cerc ca în cazul punctelor z (fiindcă z' diferă de z numai prin argumentul y, iar acesta creşte cu 2π); deducem că imaginea unei drepte verticale x = a este un cerc centrat în origine, cu raza egală cu e^a (şi pentru un segment de lungime L al acestei drepte, cercul respectiv va fi parcurs de L / 2π ori).

Interpretând pe imaginea redată mai sus, când z2 parcurge segmentul vertical [1, 1 + i π] al dreptei x = 1, exp(z2) parcurge în sens antiorar semicercul de rază e¹ = e, începând din punctul (e, 0), spre punctul (-e, 0); când z2 continuă să urce, parcurgând segmentul vertical de lungime π din banda verticală [π, 3π], exp(z2) face un "salt" din capătul (-e, 0) în (e, 0) şi reparcurge în sens antiorar semicercul anterior. Iar când z2 continuă să urce, depăşind ordonata 2π şi parcurgând segmentul de lungime π următor (până la ordonata 3π), exp(z2) parcurge în sens antiorar (dinspre capătul (-e, 0) spre (e, 0)) semicercul opus celui parcurs anterior.

În fine, să mai observăm că dreptele verticale din dreapta axei imaginare au ca imagini cercuri de raze din ce în ce mai mari (pentru că e^a creşte odată cu a, dacă a > 0), iar cele din stânga axei imaginare au ca imagini cercuri de raze din ce în ce mai mici (e^a descreşte, pentru a < 0).

Să abordăm acum cazul unei drepte orizontale, y = b. Punctele acesteia sunt z = x + i b cu x ∈ R; avem e^z = e^x e^i b, ceea ce corespunde unui vector de poziţie de lungime variabilă e^x, dar cu unghiul polar fixat b. Adică, imaginea unei drepte orizontale y = b este raza emanată din origine pe direcţia dată de Arg(b) (unghiul ei cu semiaxa reală pozitivă are măsura b radiani). Pentru b = 0 obţinem că axa reală este transformată în semiaxa reală pozitivă.

Dacă urcăm o dreaptă orizontală, începând de la axa reală şi până la înălţimea π / 2, razele corespunzătoare vor "mătura" primul cadran (dreapta y = π / 2 fiind transformată în semiaxa imaginară pozitivă); continuând deplasarea în sus până la înălţimea π, razele corespunzătoare vor mătura al doilea cadran (dreapta y = π fiind transformată în semiaxa reală negativă); analog avem pentru deplasarea în jos, începând de la axa reală.

Să considerăm acum o dreaptă oblică, având tăietura reală a şi panta m = tg(α) date (unde α este unghiul cu semiaxa reală pozitivă, diferit de 0 şi de π/2). Punctele ei sunt z = a + i m(x-a) şi avem e^z = e^x e^i m(x-a), adică în coordonate polare: ρ = e^x, θ = m(x-a); eliminând x între acestea, găsim ρ = e^a e^θ / m = e^a e^{θ ctg α} - deci transformata unei drepte oblice este o spirală logaritmică centrată în origine (vezi figura de mai sus).

Desigur că, dacă ar fi cazul - putem studia la fel, diverse alte transformări (cos(), sqrt(), ridicare la putere, funcţii omografice, etc.)

3. Transformări asupra tablei de şah

Pentru o tablă de şah este uşor să generăm o reţea de puncte care să-i reprezinte câmpurile (urmând să-i aplicăm o transformare sau alta şi să plotăm rezultatul); desigur, pentru a folosi funcţia make_grid() din §1 trebuie să obţinem întâi vectorul afixelor centrelor:

build_centers <- function(left=-pi, right=pi) {
  s <- (right - left) / 16  # semilungimea laturii câmpului
  cg8 <- seq(left + s, right - s, by=2*s)  # abscisele centrelor, pe orizontală
  cg64 <- expand.grid(cg8, cg8)  # coordonatele centrelor
  return(cg64$Var1 + 1i*cg64$Var2)
}
fields <- build_centers()  # afixele centrelor celor 64 de câmpuri

Dacă ne vom gândi să transformăm doar o anumită selecţie de câmpuri, atunci este important de reţinut ordinea în care am adăugat afixele centrelor; aici, ele sunt indexate de la stânga spre dreapta, de jos în sus (fields[1] este afixul centrului colţului stânga-jos).

Rescriem funcţia convert() din [1], prevăzând acum şi un parametru în care să putem specifica o funcţie de transformare a reţelei de puncte:

convert <- function(id_fld=1:64, fun=NULL,
                    npoints=200, file=NULL, title=NULL, ...) {
  s = fields[1] - fields[2]  # lungimea câmpului
  mesh <- sapply(fields[id_fld], function(cg) make_grid(cg, len=s, np=npoints))
  if(!is.null(fun))  # aplică transformarea indicată
      mesh <- fun(mesh)
  if(!is.null(file))
    png = png(filename = paste(file, ".png", sep=""), bg="transparent")
  opar <- par(mar=c(0, 0, ifelse(is.null(title), 0, 2), 0),
              bty="n", xaxt="n", yaxt="n")
  plot(mesh, type="n", asp=1)
  for(i in 1:length(id_fld))  # plotează câmpurile transformate (alternând culorile)
    points(mesh[, i], pch=19, cex=0.2, col = set_col(i, ...))
  if(!is.null(title))  # adaugă eventual, un titlu
    title(main=title)
  par(opar)
  if(!is.null(file)) dev.off()
}

Apelul convert() plotează tabla de şah, culorile câmpurilor fiind stabilite prin funcţia set_col() din [1] §3. Dăm alte câteva exemple de apelare, selectând eventual numai anumite câmpuri (pentru a ţine cont de particularităţile unor transformări, încât să evităm suprapunerea sau confundarea unor regiuni ale imaginii finale):

sq5 <- seq(5, 61, by=8)  # coloana a cincea a tablei
sq58 <- c(sqb, sqb+1, sqb+2, sqb+3)  # jumătatea din dreapta a tablei
convert(id = sq58, fun = exp, title="exp() pe semitabla dreaptă", file="exp58")
convert(id = sq58, fun = cos, title="cos() pe semitabla dreaptă", fi="cos58")
convert(fun = sqrt, title="sqrt()", fi="sqrt")
convert(fun = function(u) exp(sqrt(u)), title="exp(sqrt())", fi="exp.sqrt")
convert(id=c(19,22,43,46), fun=function(u) u^3, title="^3, c3-f6", fi="to3.c3f6")
convert(id=c(19,22,43,46), fun=function(u) u^5, title="^5, c3-f6", fi="to5.c3f6")
convert(id=1:16, fun=function(u) u^3.85, title="^3.85 1:16", fi="to3.85", alpha=10)

Primele două imagini reprezintă transformarea semitablei din dreapta (cele 32 de câmpuri de pe coloanele e..h) prin exp() şi respectiv, cos(); următoarele două reprezintă transformarea întregii table prin sqrt() şi respectiv, exp(sqrt()). Penultimele două reprezintă transformarea colţurilor careului c3-f3-f6-c6 prin funcţiile de ridicare la puterea a 3-a şi respectiv, a 5-a, iar ultima - transformarea primelor două linii de câmpuri prin ridicarea la o putere "extravagantă", ca 3.85; apare aici (printr-o alegere convenabilă de câmpuri) un efect care pare să fie "meritoriu", de suprapunere parţială a unor regiuni (dar alegerea culorilor lasă de dorit).

Lucrurile sunt "simple" câtă vreme transformăm o reţea de puncte "fictive" (generată printr-o funcţie ca make_grid()); cum am opera însă, dacă am vrea să transformăm o imagine reală, constând dintr-o matrice în care fiecare număr reprezintă într-un anumit mod, culoarea câte unuia dintre pixeli?