Ambiţiile Cavalerului
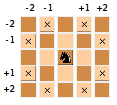 Jocul de şah prevede o piesă denumită Cal (Конь în rusă, dar Cavalier şi Knight - "cavaler", nu "cal" - în franceză şi engleză). Regula de mutare este explicitată în diagrama alăturată şi poate fi sintetizată astfel: calul poate sări de pe câmpul de coordonate
Jocul de şah prevede o piesă denumită Cal (Конь în rusă, dar Cavalier şi Knight - "cavaler", nu "cal" - în franceză şi engleză). Regula de mutare este explicitată în diagrama alăturată şi poate fi sintetizată astfel: calul poate sări de pe câmpul de coordonate (L1, C1) pe câmpul (L2, C2) dacă făcând diferenţa în valoare absolută a liniilor L1 şi L2 şi respectiv, a coloanelor C1 şi C2, se obţine sau 2 şi respectiv 1, sau 1 şi respectiv 2. O definiţie echivalentă angajează "tabloul salturilor": calul poate sări pe unul dintre cele maximum 8 câmpuri de coordonate (L1 + x, L2 + y) unde (x, y) = (-1, -2), sau (x, y) = (-2, -1), etc. (dacă acel câmp nu este în afara tablei). Vom vedea între altele că unele rezultate depind de folosirea uneia sau alteia dintre aceste definiţii echivalente.
Problema pe care o abordăm este binecunoscută (Knight_tour): calul pleacă de pe un câmp precizat şi trebuie să viziteze fiecare dintre câmpurile tablei exact o dată. Modelăm problema în termenii teoriei grafurilor şi folosim javascript şi backtracking (compus în final, cu algoritmul euristic al lui Warnsdorff).
Modelarea problemei (ca graf şi ca obiect de memorie)
Alegem un colţ al tablei; dar nu contează care, fiindcă prin rotirea tablei oricare colţ poate fi adus în poziţia stânga-sus.
Indexăm câmpurile începând din colţul stânga-sus şi continuând pe fiecare linie de la stânga la dreapta.
Indexăm de la 0 şi nu de la 1, în primul rând pentru că este firesc să asociem indecşii i = 0..n*n-1 corespunzători câmpurilor, cu intrările respective într-un tablou unidimensional T[], în care T[i] conţine o anumită informaţie privind câmpul de rang i (de exemplu, dacă există sau nu cal pe acel câmp; sau pentru alt exemplu, T[i] = numărul de ordine al acelui câmp în cadrul unui anumit traseu al calului).
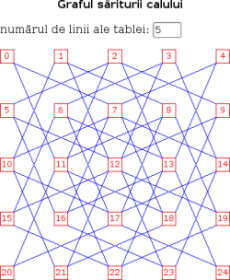
Astfel, obţinem un graf cu nodurile 0..n×n-1, în care vârfurile i şi j sunt adiacente (adică legate printr-o muchie) în acel caz în care calul poate sări de pe câmpul i pe câmpul j. De exemplu în figura alăturată, adiacenţii vârfului 0 sunt 7 şi 11; nodul 12 are 8 adiacenţi.
Problema formulată la început revine la determinarea unui drum hamiltonian în acest graf; dacă există şi dacă nodul final este adiacent celui iniţial (cel indicat în prealabil) - atunci obţinem chiar un ciclu hamiltonian.
De exemplu, pentru graful de 25 de noduri redat în figura de mai sus avem un drum hamiltonian care pleacă de pe câmpul de index 0 şi-l putem reda astfel:
tour = [ 1, 10, 15, 20, 3, 16, 21, 2, 9, 14, 11, 8, 23, 4, 19, 22, 17,
6, 13, 24, 7, 12, 25, 18, 5 ]
1 10 15 20 3 (primele 5 elemente din tabloul "tour")
16 21 2 9 14 (următoarele 5 elemente din tour[], ş.a.m.d.)
11 8 23 4 19
22 17 6 13 24
7 12 25 18 5
Pentru fiecare vârf i = 0..24, tour[i] este numărul de ordine 1..25 al săriturii calului pe câmpul de index i. Iniţial, calul este pe câmpul 0, deci tour[0] = 1; avem tour[7] = 2, deci prima săritură este de pe câmpul 0 pe câmpul 7; apoi calul mută pe câmpul 4, fiindcă avem tour[4] = 3; ş.a.m.d.

Alăturat avem o reprezentare a unui alt drum hamiltonian, de data aceasta indexând nodurile prin tabelul tour[].
Observaţie. Pentru poziţia iniţială a calului "numărul de ordine al săriturii" ar fi de fapt 0 (nu 1)… Totuşi, vom numerota săriturile începând cu 1 (pentru câmpul pe care este aşezat iniţial calul) - pentru vârfurile i prin care trece drumul vom avea tour[i] >= 1, iar pentru cele neincluse în drumul cerut vom avea tour[i] == 0.
Însă pe graful de mai sus nu există şi un drum hamiltonian care să plece din vârful 1, sau din vârful 3… Sunt 13 vârfuri cu index par (câmpuri albe) şi numai 12 vârfuri impare (negre), iar o săritură schimbă paritatea; astfel că, pe o tablă de dimensiune impară nu există drumuri hamiltoniene care să plece de pe un câmp impar (negru).
Reprezentarea vizuală a grafului în fereastra browserului
Pentru abordarea computerizată a problemelor pe grafuri, esenţială este gândirea reprezentării în memorie a grafului (prin matrice sau liste de adiacenţă, etc.). Reprezentarea nodurilor prin cerculeţe şi a muchiilor prin linii trasate pe hârtie sau pe ecran - este de obicei lipsită de importanţă pentru rezolvarea propriu-zisă, dar poate fi utilă pentru înţelegerea şi conceperea reprezentării în memorie şi poate chiar a rezolvării.
Graful săriturii calului reprodus mai sus a fost obţinut prin scripturile încorporate în pagina knight_graph.html din knight.zip. Pentru desenare în fereastra browserului am folosit funcţii (drawRect(), drawLine(), etc.) ale obiectului jsGraphics() modelat în biblioteca "wz_jsgraphics.js" (JavaScript Vector Graphics Library, a lui Walter Zorn), inclusă şi aceasta în arhiva menţionată. Următoarea funcţie este cea apelată pentru desenarea grafului săriturii calului pe o tablă N×N:
function draw_knight_graph(N) { // pentru o tablă de şah N×N var list_adj = adjacency(N); // list_adj[SQ] referă tabloul nodurilor adiacente cu SQ var cnv = document.getElementById("myCanvas"); cnv.innerHTML = ''; var jg = new jsGraphics(cnv); // obiectul care oferă funcţiile necesare desenării pe "canvas" // (from the Walter Zorn's graphics library) var dist_px = 80; // distanţa (orizontală sau verticală) între noduri vecine (default to 80px) jg.setColor("#FF0000"); // culoarea pentru desenul nodurilor (roşu) for(var i = 0; i < N; i++) { // desenează nodurile 0, 1, ..., N*N-1 for(var j = 0; j < N; j++) { jg.drawRect(i*dist_px, j*dist_px, 20, 20); // or use jg.drawEllipse(...) var vertex = j*N + i; // înscrie înăuntru indexul nodului jg.drawStringRect(""+vertex, i*dist_px, j*dist_px+1, 20, "center"); } } jg.setColor("#0000FF"); // culoarea muchiilor (albastru) for(var i=0; i < N; i++) { for(var j=0; j < N; j++) { var sq1 = i*N + j; // pentru conversia index<=>coordonate - vezi funcţia adjacency() var l1 = parseInt(sq1 / N); var c1 = sq1 % N; var la = list_adj[sq1]; for(var k=0; k < la.length; k++) { // trasează muchii spre adiacenţi ai nodului sq1 var sq2 = la[k]; var l2 = parseInt(sq2 / N); var c2 = sq2 % N; if(l1 < l2) { // numai adiacenţii aflaţi dedesubt (e suficient, datorită simetriei) if(c1 < c2) jg.drawLine(l1*dist_px+20, c1*dist_px+20, l2*dist_px, c2*dist_px); else jg.drawLine(l1*dist_px+20, c1*dist_px, l2*dist_px, c2*dist_px+20); } } } } jg.paint(); // în final "descarcă" grafica produsă, în cnv.innerHTML }
Apelurile drawRect(X, Y, 20, 20) au "desenat" pătrăţele cu latura de 20 pixeli, având colţul stânga-sus în punctul de coordonate (X, Y) (X şi Y depind de linia şi respectiv coloana pe care se află câmpul, precum şi de distanţa dist_px fixată între nodurile vecine pe orizontală sau pe verticală):
(X, Y) ———— (20+X, Y)
| |
| |
(X, 20+Y) ———— (20+X, 20+Y)
Pentru a marca adiacenţa cu un nod aflat dedesubt şi la dreapta am "unit" (folosind lineDraw()) colţul "dreapta-jos" (20+X, 20+Y) al câmpului de plecare, cu colţul "stânga-sus" al câmpului de sosire (analog pentru legătura cu un nod aflat dedesubt şi la stânga).
Observaţie. Funcţia redată mai sus nu angajează formulele caracteristice săriturii calului, adiacenţii nodurilor fiind preluaţi la debutul ei, prin var list_adj = adjacency(N); prin urmare, ea poate folosi pentru "desenarea" în fereastra browserului nu numai a grafului săriturii calului, dar a oricărui graf care are n×n vârfuri şi pentru care s-a scris o funcţie adjacency() care să returneze listele de adiacenţi corespunzătoare.
Listele de adiacenţi
În principiu, formularea rezolvării ar trebui să fie independentă de structura intrinsecă a grafului - astfel încât formularea respectivă să poată fi aplicată pe diverse structuri şi nu numai pe una specifică. În cazul de faţă, izolăm chestiunea prezentării iniţiale a grafului (prin furnizarea listelor de adiacenţă) faţă de rezolvarea propriu-zisă - programul va primi listele de adiacenţă din exterior şi va determina un drum hamiltonian în graful respectiv, chiar şi în anumite cazuri când acest graf nu este cel specific săriturii calului.
Listele de adiacenţi pentru graful desenat mai înainte pot fi reprezentate prin următorul "tablou de tablouri":
var Lists = [ [7, 11], // Lists[0] referă tabloul [7,11] - adiacenţii nodului 0 [10, 12, 8], // Lists[1][0] = 10; Lists[1][1] = 12; - adiacenţii nodului 1 [5, 11, 13, 9], // adiacenţii vârfului 2; avem Lists[2][3] = 9 // ş.a.m.d. [17, 13] // Lists[24] referă tabloul adiacenţilor nodului 24 ];
Această manieră de construcţie directă este adecvată pentru a reda un graf oarecare prin listele de adiacenţă corespunzătoare. În cazul când aceste liste trebuie generate prin program (şi nu "citite de la tastatură"), putem prefera următorul procedeu:
var Lists = new Array(); // începem cu un "tablou vid" for(var i = 0; i < 25; i++) Lists[i] = new Array(); // extinde Lists cu încă un element (anume, "tablou vid") // acum Lists.length are valoarea 25; Lists "conţine" 25 de "tablouri vide" // urmează să se determine adiacenţii şi să se adauge corespunzător în liste Lists[0].push(7); // adaugă 7 în tabloul referit de Lists[0] Lists[0].push(11); // acum Lists[0].length are valoarea 2; avem Lists[0] = [7, 11]
Pentru graful săriturii calului pe o tablă n×n reprezentat conform celor convenite mai sus, următoarea funcţie generează listele de adiacenţi:
function adj_rows(n) { // tabla de şah are dimensiunea n×n var L = new Array(); for(var i = 0, N = n*n; i < N; i++) { // n*n este calculat numai la începutul ciclului L[i] = new Array(); // pentru adiacenţii vârfului i var r1 = parseInt(i / n); // linia 0..n-1 pe care se află câmpul i var c1 = i % n; // coloana câmpului i for(var j = 0; j < N; j++) { var r2, c2, a1, a2; r2 = parseInt(j / n); // linia câmpului j c2 = j % n; // coloana câmpului j a1 = r1 > r2 ? r1 - r2 : r2 - r1; // valoarea absolută a diferenţei liniilor a2 = c1 > c2 ? c1 - c2 : c2 - c1; // valoarea absolută a diferenţei coloanelor if(((a1 == 2) && (a2 == 1)) || ((a1 == 1) && (a2 == 2))) L[i].push(j); // calul poate sări de pe câmpul i pe câmpul j } } return L; // furnizează listele de adiacenţi }
Se observă că nu s-a ţinut cont de simetria grafului nostru şi se investighează toate perechile (i, j)… Următoarea variantă este mai eficientă (pentru fiecare câmp se investighează cel mult 8 alte câmpuri, datorită implicării unui tablou constant jumps[] al celor 8 salturi posibile într-o direcţie sau alta):
function adj_jumps(n) { // tabla de şah are dimensiunea n×n var L = new Array(); var jumps = [[1,2], [2,1], [-1,2], [2,-1], [-2,1], [1,-2], [-1,-2], [-2,-1]]; for(var i = 0; i < n; i++) for(var j = 0; j < n; j++) { var ind = i*n + j; // indexul câmpului aflat pe linia i şi coloana j L[ind] = new Array(); // pentru lista adiacenţilor nodului for(var k = 0; k < 8; k++) { // pentru toate săriturile posibile var i1 = i + jumps[k][0]; // linia câmpului pe care sare calul if((i1 >= 0) && (i1 < n)) { // dacă linia destinaţie este interioară tablei var j1 = j + jumps[k][1]; // coloana câmpului destinaţie if((j1 >= 0) && (j1 < n)) // când coloana este interioară tablei L[ind].push(i1 * n + j1); } } } return L; // furnizează listele de adiacenţi }
Am formulat mai sus două variante pentru determinarea listelor de adiacenţi, dar nu pentru a compara complexitatea calculului - oricum funcţia va fi executată o singură dată (la debutul programului de găsire a unui drum hamiltonian). Ambele funcţii sunt utile pe parcursul experimentelor, pentru motivul că ordinea în care sunt găsiţi şi memoraţi adiacenţii diferă între cele două variante; ori, tratând problema prin backtracking, ordinea abordării succesorilor determină atât viteza cu care se obţine soluţia, cât şi constituţia soluţiei.
Modelarea căutării unui drum hamiltonian
În general, o aplicaţie pentru browser este compusă din fişiere HTML, CSS şi Javascript - în ideea de a separa prezentarea (pentru care folosim de obicei HTML şi CSS) de funcţionalitatea specifică (pentru care folosim JS). Fişierul HTML trebuie să conţină (eventual) elementele necesare introducerii datelor şi să apeleze funcţiile de prelucrare existente în fişierul JS; simplificând probabil la maximum, specificaţia unui fişier HTML care la încărcarea în browser să rezolve problema noastră, poate arăta astfel:
<head> <script src = "knight-lib.js"></script> <!-- încarcă fişierul de funcţii JS --> </head> <body> <script> var prob1 = new knightPath(5, 0); // instanţiază şi rezolvă pe tabla 5×5, din câmpul 0 var prob2 = new knightPath(6, 3); // instanţiază şi rezolvă pe tabla 6×6, din câmpul 3 </script> </body>
Fişierul HTML redat mai sus conţine de fapt numai două elemente <script> (şi desigur <head> şi <body>, dar nu alte elemente), având deci numai rolul de a încărca şi lansa funcţiile JS; primul <script> determină browserul să încarce de pe server fişierul knight-lib.js, iar cel de-al doilea instanţiază (apelând la operatorul nativ new) obiectul knightPath() - obiect care (nefiind unul nativ, precum Array()) se presupune că este definit în cadrul fişierului JS tocmai încărcat.
Obiectul JS care "rezolvă problema" cum am zis mai sus poate fi definit începând cu şablonul următor:
function knightPath(rows, start_node, func_adj) { // func_adj referă o funcţie externă care this.rows = rows; // returnează tabloul listelor de adiacenţi this.size = rows * rows; this.lists = func_adj(rows); // preia listele de adiacenţă (aplicând funcţia indicată la apel) this.path = new Array(this.size); // path[i] = d <=> nodul i este atins la pasul d this.find_path(start_node, 1); // paşii consecutivi pe un drum hamiltonian };
La instanţiere (vezi mai sus var prob1 = new knightPath), obiectul îşi execută în final funcţia proprie find_path() (vezi ultima linie din definiţia obiectului). Adăugăm acum această funcţie, prin intermediul proprietăţii prototype (prevăzută de Javascript în scopul extinderii unui obiect cu noi proprietăţi sau metode):
knightPath.prototype.find_path = function(square, depth) { this.path[square] = depth; // pe square se ajunge la al depth-lea pas if(depth == this.size) { // dacă s-a găsit un drum hamiltonian this.dump(); // afişează drumul găsit throw "done"; // "exit(1)" - abandonează căutarea unei alte soluţii } var lad = this.lists[square]; // lista adiacenţilor nodului curent var ln = lad.length; // numărul de adiacenţi for(var i = 0; i < ln; i++) { // pentru fiecare adiacent var next_sq = lad[i]; if(!this.path[next_sq]) // dacă nu s-a trecut anterior prin adiacentul curent this.find_path(next_sq, depth + 1); // încearcă extinderea de la acest adiacent } this.path[square] = 0; // În cazul când extinderea prin adiacenţii nodului curent a eşuat // (întâlnind un nod care nu mai are adiacenţi ne-vizitaţi) // disponibilizează din nou nodul (marcându-i 0 în path[]) şi revine // la un nod anterior, în vederea încercării unui alt traseu. };
În cazul când se găseşte un drum hamiltonian (vezi linia a 3-a), obiectul nostru îşi apelează metoda dump(); aceasta trebuie să afişeze cumva, drumul găsit în path[]. De dorit ar fi desigur, ca dump() să înscrie în documentul HTML din care s-a instanţiat obiectul nostru, chiar o tablă de şah "veritabilă", pe care să plimbe o imagine de cal conform drumului găsit; dar cel puţin până punem la punct funcţionarea, ne putem mulţumi să procedăm ca într-un program C obişnuit: afişăm pe ecran (în speţă, într-o boxă de mesaj-text, folosind alert()):
knightPath.prototype.dump = function() { var html = ''; //'path = ['+ this.path + ']\n\n'; var n = this.rows; for(var i = 0; i < this.size; i += n) { // parcurge path[] din n în n, for(var j = 0; j < n; j++) // "afişând" câte n valori pe fiecare linie html += this.path[i+j] + '\t'; html += '\n'; } alert(html); };
Pentru aplicaţii este recomandabil să se folosească fişiere separate (pentru funcţiile Javascript, pentru eventuale definiţii de stiluri CSS şi respectiv pentru HTML). Dar pentru o aplicaţie de mică dimensiune poate fi comod să încorporăm toate părţile într-o singură pagină; e drept că aici, raţiunea principală a acestei unificări nu este "comoditatea"; dacă aplicaţia respectivă (şi mică) trebuie accesată oarecum independent, dintr-un site care deja are multe asemenea aplicaţii, atunci acelaşi principiul separării (de data aceasta - între aplicaţii) induce soluţia unificării componentelor acelei aplicaţii.
Studiul rezultatelor
În cazul nostru, rezultatele depind de dimensiunea tablei (nu neapărat "proporţional"), de câmpul de start al calului şi - cum am evidenţiat anterior - de funcţia de adiacenţă folosită; prin urmare, pagina HTML trebuie să conţină trei elemente <input>, pentru specificarea acestor trei parametri.
În continuare, redăm şi interpretăm câteva rezultate ale aplicaţiei de pe pagina knight-test2.html care se găseşte în arhiva knight.zip referită mai sus.
tabla 6×6, câmp iniţial 3,
cu adj_rows(): cu adj_jumps():
22 13 4 1 24 15 34 25 16 1 32 23
5 2 23 14 7 36 17 30 33 24 15 2
12 21 6 3 16 25 26 35 18 31 22 13
31 28 19 10 35 8 29 10 27 14 3 6
20 11 30 33 26 17 36 19 8 5 12 21
29 32 27 18 9 34 9 28 11 20 7 4
Am obţinut drumuri diferite, iar în primul caz am obţinut chiar un ciclu hamiltonian (de pe câmpul final 36 se poate sări pe cel iniţial). Explicaţia obţinerii de drumuri diferite constă în faptul că în listele constituite ordinea respectivilor adiacenţi diferă într-un caz faţă de celălalt; ca urmare, ordinea abordării succesorilor în mecanismul backtracking diferă şi ea, determinând extinderi diferite ale traseului şi în final - soluţii diferite.
Timpii de lucru depind foarte mult de câmpul de start şi - iarăşi - de funcţia de generare a adiacenţilor:
tabla n×n câmp iniţial adiacenţă timp aprox. (Firefox)
8×8 0 adj_rows() 30s
adj_jumps() 80s
31 adj_rows() 5s
adj_jumps() enorm
7×7 0 adj_rows() 1s
adj_jumps() 120s
9×9 0 adj_rows() 120s
Se constată că dintre cele două funcţii de generare a listelor de adiacenţă, mai avantajos de folosit este prima, adj_rows() - cea care investiga toate perechile de câmpuri. A doua funcţie - întâlnită într-o formulare sau alta în diverse alte locuri - determină direct (în fond, mai eficient decât considerarea tuturor perechilor de vârfuri) cele maximum 8 câmpuri pe care poate sări calul, folosind în acest scop un tablou constant de salturi; ordinea indusă în lista adiacenţilor unui vârf este fixată de ordinea dată a componentelor tabloului de salturi.
În adj_jumps() tabloul de salturi jumps[] are componentele date într-o ordine arbitrară; putem interveni şi să schimbăm ordinea urmând de exemplu această regulă: indicăm cele 8 salturi în sensul orar, începând cu cel mai din stânga câmp pe care poate sări calul:
function adj_jumps(n) { var L = new Array(); // var jumps = [[1,2],[2,1],[-1,2],[2,-1],[-2,1],[1,-2], // [-1,-2],[-2,-1]]; // tabloul original de salturi var jumps = [[-1,-2],[-2,-1],[-2,1],[-1,2],[1,2],[2,1], [2,-1],[1,-2]]; // iar acum, ordonate în sens orar ... }
Pare aceasta o diferenţă minoră, între prima şi a doua variantă de jumps[] - dar executând aplicaţia după ce am făcut modificarea tocmai indicată, putem constata în unele cazuri, diferenţe uriaşe de timp:
1 30 39 28 25 18 21 // cu versiunea jumps[] originală
38 49 2 19 22 27 24 // (ordine arbitrară a salturilor)
31 40 29 26 3 20 17 // Timp (Firefox): 130s
48 37 32 41 16 23 4
45 42 47 34 7 10 13
36 33 44 15 12 5 8
43 46 35 6 9 14 11
1 18 15 8 3 12 49 // cu jumps[] modificat
20 7 2 17 14 9 4 // (salturi ordonate în sens orar)
31 16 19 6 11 48 13 // Timp (Firefox): 2s (!)
40 21 30 47 24 5 10
29 32 41 22 37 46 25
42 39 34 27 44 23 36
33 28 43 38 35 26 45
Însă diferenţele de timp pot fi şi în favoarea celeilalte variante; de exemplu, pe tabla 8×8 şi câmpul de plecare 0 varianta jumps[] originală (cu salturi arbitrare) dă soluţia în circa 80s, iar varianta modificată (salturi ordonate în sens orar) o dă într-un timp enorm (o fi răbdarea un atribut necesar muncii de testare, dar…).
Obs. Timpii menţionaţi (orientativ) mai sus, corespund Firefox-ului de prin 2008-2009.
Până în acest punct, aplicaţia noastră este nesatisfăcătoare: obţinem un drum hamiltonian, dar într-un timp de lucru care pentru unele câmpuri de plecare este "enorm" (chiar pentru table 6×6, nu mai zicem de 8×8 sau mai mari); în plus, ca să obţinem rezultatul în unele cazuri, mai trebuie şi să încercăm pe rând una dintre cele trei funcţii de generare a listelor de adiacenţă.
Observaţia cea mai importantă pe care am făcut-o (şi pe care - mânat de raţiuni didactice, desigur - am şi strecurat-o anticipativ mai sus, în mai multe locuri) este aceasta: atât drumul final (aspect mai puţin important acum) cât şi timpul de lucru depind esenţial de funcţia folosită pentru generarea listelor de adiacenţă — mai precis, depind de ordinea adiacenţilor în lista corespunzătoare unui nod.
Funcţia adj_rows() înregistra adiacenţii în lista unui nod în aceeaşi ordine în care s-ar parcurge linia acelui nod în matricea de adiacenţă a grafului, urmărind de la stânga la dreapta valorile "1"; funcţia adj_jumps() înregistra adiacenţii în lista unui nod în ordinea preexistentă a salturilor înscrise în tabloul constant jumps[].
În ambele cazuri este vorba de o ordonare de natură statică; backtracking-ul a fost formulat artificial şi operează "mecanic": angajează mereu acel succesor pe care i l-a fixat din capul locului, funcţia de adiacenţă (încât totul depinde de aceasta). Ori o formulare decentă a metodei backtracking trebuie să rezerve ceva loc şi pentru o eventuală euristică, prin care să se poată alege în mod dinamic succesorul cel mai potrivit dintre cei existenţi (procesul devenind aproape "independent" de funcţia de generare iniţială a adiacenţilor; "aproape", pentru că pot exista succesori "la fel de buni" şi atunci ordinea lor rămâne aceea iniţială).
Există câteva principii euristice care se pot folosi fie ca atare (independent de vreun mecanism backtracking), fie ca parte a unei formulări backtracking. Cel mai elementar este acesta: continuă pe acel drum din care vei avea cât mai puţine ramificaţii; acest principiu decurge iterând această recomandare evidentă (sau înţeleaptă): dacă ai de ales între a face un ultim pas până la destinaţie şi respectiv a ocoli, atunci încearcă mai întâi prima variantă.
Backtracking compus cu algoritmul lui Warnsdorff
Warnsdorff în 1823 a anticipat cu mult principiul euristic tocmai amintit mai sus, formulându-l astfel (pentru tabla de şah): alege de fiecare dată acel câmp de pe care calul ar avea cel mai mic număr de noi sărituri posibile. Această idee singură (fără backtracking - a vedea programul C prezentat în Knight_tour), dă rezultate excelente pe tabla obişnuită 8×8 (şi pe multe alte cazuri); dar se pot evidenţia situaţii (chiar şi pe o tablă mică, 6×6) când drumul returnat este incomplet (există câmpuri prin care calul nu a trecut), iar aceasta se datorează faptului că la un moment dat este posibil ca mai multe câmpuri să aibă o aceeaşi valoare a "celui mai mic număr de noi sărituri" şi pe de altă parte - tocmai fiindcă nu s-a implicat şi backtracking - nu există reveniri.
Prin urmare, tot ce rămâne de făcut pentru a trece aplicaţia noastră de la "nesatisfăcător" la "onorabil" este să rescriem partea de backtracking, încorporându-i principiul euristic al lui Warnsdorff:
knightPath.prototype.grad = function(node) { // "gradul" unui nod încă nevizitat var count = 0; for(var i = 0, n = this.lists[node].length; i < n; i++) if(!this.path[this.lists[node][i]]) count++; return count; // numărul de câmpuri nevizitate, adiacente cu nodul dat }; knightPath.prototype.find_path = function(square, depth) { this.path[square] = depth; // pe square se ajunge la al depth-lea pas if(depth == this.size) { // dacă s-a găsit un drum hamiltonian this.dump(); // afişează drumul găsit throw "done"; // "exit(1)" - abandonează căutarea unei alte soluţii } var lad = this.lists[square]; // lista adiacenţilor nodului curent var ln = lad.length; // numărul de adiacenţi ai nodului curent for(var x = 0; x < ln - 1; x++) // ordonează adiacenţii, crescător după grad() for(var y = x+1; y < ln; y++) if(this.grad(lad[x]) > this.grad(lad[y])) { var aux = lad[x]; lad[x] = lad[y]; lad[y] = aux; } for(var i = 0; i < ln; i++) { // pentru fiecare adiacent var next_sq = lad[i]; if(!this.path[next_sq]) // nu s-a trecut anterior prin adiacentul curent this.find_path(next_sq, depth + 1); // încearcă extinderea de la acest adiacent } this.path[square] = 0; // în cazul când extinderea prin adiacenţii nodului curent a eşuat };
În loc să furnizăm direct "acel câmp de pe care calul ar avea cel mai mic număr de noi sărituri posibile", a fost parcă mai simplu să ordonăm "crescător după grad()" tabloul adiacenţilor; iar pentru ordonare a fost iarăşi mai simplu, să folosim "bubble-sort" decât metoda sort() a obiectului JS Array(). Sortarea va fi operată de multe ori (dar pe tablouri foarte mici), însă acest fapt n-ar avea de ce să fie important de vreme ce vrem să obţinem un singur drum (nu pe toate).
Pagina creată astfel knight-test3.html se găseşte în arhiva "knight.zip" referită mai sus. Drumurile rezultate depind de funcţia de adiacenţă folosită (pentru motivul că sortarea specificată mai sus nu schimbă ordinea iniţială a adiacenţilor, dacă aceştia au acelaşi "grad()). Drumul nu se poate obţine pentru table mai mari decât 50×50 (depinzând şi de browser) - va rezulta eroarea too much recursion.
Timpii de execuţie depind de asemenea, de funcţia de adiacenţă: când se foloseşte prima definiţie de adiacenţă (cea care simula ordinea din matricea de adiacenţă) obţinem - sub Firefox - 5 secunde pentru tabla 30×30, 10 secunde pentru 40×40, 20 secunde pentru 50×50; în schimb, folosind funcţia a treia (bazată pe tabloul salturilor ordonate în sens orar) - timpul este de una-două secunde cam indiferent de tipul tablei (pe 50×50, câmp iniţial 1249, funcţia 3: circa 2 secunde).
Vizualizarea drumului
În final, se pune şi problema de a vizualiza drumul obţinut. Pentru aceasta, procedăm ca la "Reprezentarea vizuală a grafului în fereastra browserului":
knightPath.prototype.draw = function() { var cnv = document.getElementById("myCanvas"); cnv.innerHTML = ''; // "şterge" precedentul grafic (dacă există) var jg = new jsGraphics(cnv); var rows = this.rows; var n = this.path.length; // lungimea drumului var dist_px = 80; // 80px între noduri (orizontal, vertical) jg.setColor("#FF0000"); for(var i = 0; i < rows; i++) // desenează pătrăţelele for(var j = 0; j < rows; j++) jg.drawRect(i*dist_px, j*dist_px, 20, 20); var tu_sq = {}; // pentru "inversarea" funcţiei path[câmp] = numărul săriturii for(var i = 0; i < n; i++) tu_sq[this.path[i]] = i; // rangului săriturii i se asociază câmpul pe care sare var sq1, l1, c1, sq2, l2, c2; for(var i = 1; i < n; i++) { jg.setColor("#0000FF"); sq1 = tu_sq[i]; // câmpul de pe care se execută săritura a i-a l1 = parseInt(sq1 / rows); c1 = sq1 % rows; sq2 = tu_sq[i+1]; // câmpul pe care se sare a (i+1)-a oară l2 = parseInt(sq2 / rows); c2 = sq2 % rows; // trasează muchia care uneşte cele două câmpuri jg.drawLine(l1*dist_px+10, c1*dist_px+10, l2*dist_px+10, c2*dist_px+10); // înscrie indexul câmpului în pătrăţelul al i-lea jg.setColor("#000000"); jg.drawStringRect(""+i, l1*dist_px, c1*dist_px+1, 20, "center"); } sq1 = tu_sq[1]; l1 = parseInt(sq1 / rows); c1 = sq1 % rows; sq2 = tu_sq[n]; l2 = parseInt(sq2 / rows); c2 = sq2 % rows; // înscrie indexul ultimei sărituri în patrăţelul final al drumului jg.drawStringRect(""+n, l2*dist_px, c2*dist_px+1, 20, "center"); // marchează pe desen nodul de start şi nodul final ("bold") jg.setColor("#0000FF"); jg.setStroke(2); jg.drawRect(l1*dist_px, c1*dist_px, 20, 20); jg.drawRect(l2*dist_px, c2*dist_px, 20, 20); jg.paint(); };
Desigur că, în cadrul funcţiei find_path() invocăm fie funcţia iniţială dump(), fie funcţia draw() - depinzând de dimensiunea tablei:
if(depth == this.size) { // dacă s-a găsit un drum hamiltonian if(this.rows > 10) this.dump(); // "alert" drumul găsit, pe table mai mari ca 9×9 else this.draw(); // chiar desenează drumul, pe table mai mici ca 10×10 throw "done"; // "exit(1)" - abandonează căutarea unei alte soluţii }
Cu această ultimă completare (plus alte câteva ajustări care se pot vedea pe sursă), pagina respectivă knight-test4.html se găseşte în arhiva knight.zip.
vezi Cărţile mele (de programare)