În [1] am ajuns (treptat) la o gramatică de recunoaştere a expresiilor aritmetice şi - parametrizând neterminalii prin constructori de arbori - am obţinut arborele sintactic corespunzător unei expresii date; în [2] am procedat "pe dos" - am constituit un model de arbore sintactic şi bazat pe acesta, am generat arbori aritmetici (expresii) de un anumit tip (de valoare dată):

?- expr(Tree, [6, /, '(', 1, -, 3, /, 4, ')'], []). % expresia dată: 6/(1-3/4) (Prolog)
Tree = div(6, sub(1, div(3, 4))) . % arborele sintactic al expresiei date

Tree t = Tree('/', 6, Tree('-', 1, Tree('/',3,4))); // instanţă C++ de arbore (sintactic)
(6/(1-(3/4))) = 24 // expresia şi valoarea arborelui instanţiat de utilizator

Reluăm modelarea arborilor aritmetici, vizând acum nu numai (ca în [2]) furnizarea expresiei care corespunde arborelui deja instanţiat într-o funcţie a utilizatorului, dar şi invers - instanţierea acelui arbore care corespunde unei expresii date; dar această "inversare" nu are aplicaţii semnificative - servind numai pentru a prelua din exterior o expresie în format obişnuit şi a o transforma într-o structură de date (aceasta - Tree - ar servi eventual pentru aplicaţii, ca în [2]), structură care de fapt putea fi instanţiată direct, în programul respectiv.

Spre deosebire de [1], acum vom explicita şi exploata în mod direct proprietăţile operatorilor - în mecanismele gramaticale tipice, acestea sunt internalizate şi figurează în mod implicit, iar în partea finală din [1] am evidenţiat defectul de eficienţă rezultat astfel şi am învederat ca soluţie tocmai explicitarea priorităţii şi asocierii.

Exemplificare (arbore aritmetic şi format de afişare)

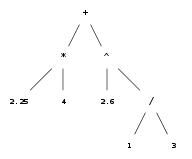
Am vizualizat aici un "arbore aritmetic", să-i zicem T. Rădăcina lui este operatorul +, având ca fii un sub-arbore T1 de rădăcină * (care are ca fii operanzii 2.25 şi 4) şi un sub-arbore T2 de rădăcină ^.

    + * 2.25 4 ^ 2.6 / 1 3   // formatul prefixat
    ((2.25 * 4) + (2.6 ^ (1 / 3)))  // infixat (şi parantezat)
    2.25 4 * 2.6 1 3 / ^ +  // postfixat
    10.3751  // valoarea numerică a arborelui

După ordinea în care citim, avem formatul prefixat T = (+, T1, T2), cu T1 = (*, 2.25, 4) şi T2 = (^, 2.6, T3 = (/, 1, 3)); sau avem format postfixat T = (T1', T2', +), sau infixat T = (T1'', +, T2'').

Abstractizarea nodurilor arborelui

Pentru a obţine formatul textual şi valoarea numerică asociată arborelui - înzestrăm fiecare nod al arborelui cu metodele print() şi eval(); dar acestea vor trebui să opereze după caz: pentru un nod "frunză" (care corespunde unui operand numeric), print() va trebui să afişeze valoarea respectivă - dar pentru un nod intern (rădăcină de sub-arbore, corespunzând unui operator) print() va trebui (pe lângă afişarea ca atare a operatorului respectiv) să apeleze metodele print() ale celor doi fii.

Este firesc ca urmare, să considerăm un şablon abstract tNode, pentru nodurile arborelui ArTree:

#include <ostream>
#include <memory>  // std::shared_ptr ("smart pointers", C++11)
class ArTree; // va modela "arborii aritmetici"
class tNode { // şablon pentru nodurile arborelui aritmetic (operanzi, operatori)
    // ArTree (metodele interne şi "<<") trebuie să acceseze tNode
    friend class ArTree;
    friend std::ostream& operator<<(std::ostream&, const ArTree&);
protected:
    virtual double eval() const =0;
    virtual void print(std::ostream&) const =0;
};

Vom prevedea ca fiecare arbore (sub-arbore) T - instanţă a clasei ArTree - să conţină ca dată internă, un pointer _root la obiectul tNode corespunzător rădăcinii arborelui; T._root -> print() va invoca metoda print() specifică nodului respectiv - iar aceasta va apela mai departe metodele print() ale subarborilor stâng şi drept, prin intermediul pointerilor existenţi în fiecare subarbore.

Bineînţeles că pentru afişare, vom supraîncărca operatorul <<; relaţia "friend" nu este tranzitivă, aşa că această re-definire trebuie declarată friend şi în clasa tNode (nu numai în ArTree) - pentru ca << să poată accesa metodele print() ale nodurilor (acestea nefiind "publice"). La fel, ArTree trebuie declarată friend în tNode - pentru ca _root -> eval() să poată apela metodele eval() ale nodurilor.

Dacă am folosi pointeri obişnuiţi (folosind explicit new()), ar trebui să completăm clasa tNode cu un destructor virtual (apelând explicit delete); însă preferăm să folosim smart pointers (din C++ 11) - incluzând deci <memory>.

Înscriem secvenţa redată mai sus în fişierul arithtree.h. Ar urma să adăugăm definiţiile nodurilor propriu-zise - derivate din clasa de bază tNode tocmai constituită; dar dintre cele două tipuri de noduri, Operator implică obiecte ArTree (construind cei doi subarbori) - astfel că este obligatoriu să formulăm întâi ArTree (şi după aceea, să adăugăm Operator).

Constituţia arborelui aritmetic

Un arbore este reprezentat de rădăcina sa: câmpul privat _root pointează obiectul tNode aferent nodului rădăcină. Un arbore poate să fie "vid" - rădăcina este nullptr (pointer nul), neindicând nicio instanţă tNode; poate să fie constituit dintr-un singur nod, reprezentând un "operand" - _root referă atunci obiectul tNode prin care este reprezentat operandul; sau poate să aibă doi fii, care sunt şi ei arbori - integrând astfel un "operator":

class ArTree {  // arbori (şi sub-arbori) aritmetici
public:
    ArTree(): _root(nullptr) {}

    ArTree(double); // construieşte un Operand numeric
    ArTree(char, ArTree, ArTree); // integrează un Operator (sub-arbore)

    double eval() const { return _root -> eval(); }

    static int format; // prefixat, infixat, postfixat
    static void set_format(int f) { format = f; }

private:
    std::shared_ptr<tNode> _root; // pointer la rădăcina (sub)arborelui

friend std::ostream& operator<<(std::ostream&, const ArTree&);
};

inline std::ostream& operator<<(std::ostream& out, const ArTree& T) {
    T._root -> print(out);
    return out;
}

Dintr-un obiect ArTree aferent unui operand, eval() va returna valoarea numerică a operandului respectiv; însă dintr-o instanţă de operator, eval() va constitui valoarea corespunzătoare arborelui din valorile obţinute prin apelarea metodelor eval() ale celor doi subarbori ai săi ("recursivând" astfel, până la nivelul operanzilor).

La fel decurg lucrurile, în privinţa afişării (regizată în modul obişnuit, supraîncărcând operator<<) - folosind metodele print() ale nodului-rădăcină şi ale subarborilor. Câmpul format este declarat static, încât odată stabilit un format de afişare - acesta va fi cel avut în vedere de metodele print() ale tuturor nodurilor constituente.

Modelarea operanzilor şi operatorilor

După cum ne alegem "operanzii" şi "operatorii" pe care îi are în vedere la nivel generic ArTree - vom avea o categorie sau alta, de arbori sintactici. Ca idee - am putea considera cuvinte obişnuite, iar ca operatori - anumite funcţii de câte două argumente, adecvate contextului acestor cuvinte.

Pentru expresiile aritmetice, operanzii sunt valori numerice imediate:

class Operand: public tNode { // operanzi numerici
public:
    Operand(double number) : number(number) {}
private:
    double number;
    double eval() const { return number; }
    void print(std::ostream& out) const { out << number; }
};

La prima vedere, această definiţie nu are de-a face cu ArTree… Constructorul fiind declarat "public" - vom putea folosi de exemplu Operand x(3.14);. Dar obiectul x construit astfel va fi inaccesibil, dat fiind că membrii săi sunt instituiţi cu "private" - iar în această situaţie construcţia respectivă nu mai are sens şi era chiar cazul de a o interzice, declarând şi constructorul cu "private".

Însă în principiu, operanzii şi operatorii trebuie văzuţi în contextul arborelui (ca noduri ale acestuia); anticipând puţin, construcţia ca ArTree a unui nod foloseşte metoda (din <memory>) make_shared() (de exemplu, make_shared<Operand>(3.14)), metodă care va construi ea însăşi obiectul de tipul indicat - impunând astfel prevederea de constructori "public" (de Operand şi de Operator).

Este pe deplin suficient, să considerăm numai operatori binari:

class Operator: public tNode { // operatori aritmetici binari
public:
    Operator(char binop, ArTree left, ArTree right)
        : binop(binop), left(left), right(right) {}
private:
    char binop;
    ArTree left, right;
    double eval() const;
    void print(std::ostream&) const;
};

Desigur, n-avem decât să imităm definiţia de mai sus (adăugând o clasă "UnaryOperator") dacă am vrea să considerăm şi vreun operator "unar"… Este drept că aceasta ar putea fi necesar, de exemplu pentru expresii ca -(...), sau +(...) - dar o simplă schimbare de semn nu prea merită atenţie.

Am evidenţiat deja că nu are sens să instanţiem ca atare, operanzi şi operatori; în schimb, vom putea să-i construim şi să-i folosim ca obiecte ArTree - de exemplu astfel:

ArTree x(3.14), y(2); // construieşte operanzii x, y
ArTree div('/', x, y); // construieşte operatorul '/' (fracţia x/y)
ArTree::set_format(1); // setează formatul infixat
std::cout << div << " = " << div.eval(); // (3.14 / 2) = 1.57

Constructorii de arbori; metodele operatorilor

Implementăm constructorii prevăzuţi de clasa ArTree, precum şi metodele print() şi eval() ale operatorilor, într-un fişier arithtree.cpp:

#include "arithtree.h"
#include <cmath> // pow() (pentru operatorul '^')

ArTree::ArTree(double number)
    : _root(std::make_shared<Operand>(number)) {}

ArTree::ArTree(char binop, ArTree left, ArTree right)
    : _root(std::make_shared<Operator>(binop, left, right)) {}

int ArTree::format = 0; // iniţializează formatul de afişare (anume, "prefixat")

make_shared<T>(listă_parametri) gestionează alocarea dinamică a memoriei (în cursul execuţiei) pentru un obiect de tip T (pentru Operand, respectiv Operator): va aloca memorie (apelând operatorul new()) şi va lansa constructorul T(listă_parametri), presupus a fi unul public; va returna un obiect de tip shared_ptr<T>, care păstrează un pointer la obiectul alocat şi un contor intern use_count() al referirilor la acel obiect. use_count este iniţializat cu 1 în momentul construcţiei obiectului şi este incrementat de exemplu când se creează o "copie" temporară a obiectului (ca variabilă locală unei funcţii), fiind decrementat apoi când blocul în care a fost referit este distrus; iar când "use_count" devine 0 - obiectul respectiv este dealocat (implicând operatorul delete).

Câmpul format a fost declarat static, în clasa ArTree - el nu este membru propriu-zis (precum _root) al vreunei instanţe şi deci, nu este şi alocat în memorie în momentul construirii unui obiect ArTree; din acest motiv - am iniţializat (în exteriorul clasei) int ArTree::format = 0.

În sfârşit, adăugăm în arithtree.cpp definiţii pentru metodele operatorilor:

void Operator::print(std::ostream& out) const { 
    switch(ArTree::format) {
        case 1: // infixat
            out << '(' << left << ' ' << binop << ' ' << right << ")"; break;
        case 2: // postfixat
            out << left << ' ' << right << ' ' << binop << ' '; break;
        default: // prefixat
            out << binop << ' '<< left << ' ' << right << ' ' ;
    }
}
double Operator::eval() const {
    double val_1 = left.eval(); // evaluează subarborele stâng
    double val_2 = right.eval(); // evaluează subarborele drept
    switch(binop) {  // sintetizează valoarea finală
        case '+': val_1 += val_2; break;
        case '-': val_1 -= val_2; break;
        case '*': val_1 *= val_2; break;
        case '/': val_1 /= val_2; break; // ignoră excepţia val_2==Zero
        case '^': val_1 = pow(val_1, val_2); break; // ignoră unele excepţii
    }
    return val_1;
}

Pentru cazul "infixat" (în print()) a trebuit să parantezăm expresia aferentă arborelui (sub-arborelui): pentru a fi evitat parantezele inutile, era necesar să avem în vedere în mod explicit priorităţile operatorilor - complicând inutil lucrurile (nu acest format comun interesează…).

În eval() am preferat să ignorăm cazurile de excepţie tipice (precum "Divide By Zero"); în funcţie de compilatorul folosit, în aceste cazuri va rezulta "runtime error", sau dimpotrivă - expresia va fi totuşi evaluată, ca inf ("infinit").

Arborele (obiect ArTree) corespunzător unei expresii date

Nu mai dăm aici un exemplu de exploatare, a claselor constituite mai sus în fişierele arithtree.h şi arithtree.cpp; acestea diferă totuşi nesemnificativ, faţă de cele specificate în [2] - unde am ilustrat deja folosirea acestor clase: am generat folosind ArTree ("Tree", în notaţiile din [2]) toate expresiile aritmetice care angajează patru operanzi daţi şi trei operatori (putând apoi filtra din fişierul rezultat, de exemplu acele expresii care se evaluează pe o valoare dată).

Având modelarea de mai sus pentru arborii sintactici - să punem acum şi problema oarecum inversă: preluând o expresie aritmetică în formatul infixat obişnuit, să obţinem obiectul ArTree corespunzător acesteia.

Parametrizarea construcţiei arborilor, după proprietăţile operatorilor

Să considerăm câteva expresii aritmetice tipice şi să vedem cum putem construi obiectele ArTree corespunzătoare lor. Cazurile semnificative angajează măcar trei operanzi.

Expresia a - b + c angajează doi operatori de acelaşi nivel de prioritate şi ambii au asociere-stânga. Analiza care conduce la obiectul ArTree corespunzător ar decurge astfel: citim primul operand, a şi invocăm constructorul ArTree de "Operand" - ArTree t1(a); citim operatorul '-', apoi şi operandul b, pentru care creem ArTree t2(b); citim apoi următorul operator, '+' şi fiindcă acesta nu are prioritate mai mare decât precedentul (însemnând că 'b' trebuie "legat" de 'a' şi nu de 'c') - construim ArTree t3('-', t1, t2), pentru subexpresia a - b; în final - citim c şi creem ArTree t4(c), iar apoi construim rezultatul ArTree T('+', t3, t4).

Pentru a - b * c, după ce se creează t1 şi t2 - se citeşte '*', de prioritate mai mare decât precedentul operator ('b' trebuie "legat" de 'c' şi nu de 'a'); în acest caz, trebuie să amânăm construcţia arborelui de rădăcină '-' (precedentul operator), salvând cumva contextul respectiv; citim c, creem ArTree t3(c) şi ArTree t4('*', t2, t3) - apoi restaurăm contextul arborelui de rădăcină '-' şi definitivăm construcţia acestui arbore prin ArTree T('-', t1, t4).

Pentru a ^ b ^ c lucrurile decurg la fel ca pentru "a-b*c", dar nu din cauza diferenţei de prioritate între operatori, ci fiindcă '^' asociază la dreapta: ArTree('^', t1, t4), cu Artree t4('^', t2, t3).

Având de ţinut seama de prioritatea operatorilor şi având de salvat temporar anumite contexte de lucru - să ne imaginăm o funcţie recursivă parse(level), având ca parametru prioritatea curentă; caracterul recursiv asigură în mod implicit, salvarea şi restabilirea datelor locale (prin "cadrele stivă" corespunzătoare apelurilor respective).

În principiu (sau "în fugă"…), parse(P) va fi apelată pentru fiecare operator întâlnit prin parcurgerea expresiei şi putem avea două situaţii: dacă acesta are prioritatea mai mică decât P ("prioritatea curentă" a apelului), atunci putem încheia construcţia subarborelui - revenind din apelul curent la cadrele-stivă anterioare, unde regăsim (din cursul apelurilor petrecute) primul operand şi operatorul corespunzător nivelului P (al doilea operand fiind obţinut la debutul apelului curent).

În schimb, dacă prioritatea operatorului întâlnit este cel puţin P, atunci nu mai putem încheia construcţia subarborelui: s-ar putea ca operandul tocmai citit să trebuiască "legat" la dreapta (şi nu de contextul apelurilor anterioare) - cum este cazul expresiilor a + b*c, sau ca în a^b^c; în acest caz, va trebui reapelată parse(P1), unde P1 este fie chiar prioritatea operatorului tocmai întâlnit dacă acesta este '^' (trebuind să verificăm dacă după primul '^' urmează şi un al doilea '^', dat fiind că '^' asociază la dreapta) - fie, cu 1 mai mare decât prioritatea operatorului tocmai întâlnit (trebuind să verificăm dacă după acesta urmează sau nu, un operator de prioritate mai mare ca a lui).

Modelarea analizei ghidate de proprietăţile operatorilor

Din ArTree derivăm o clasă Climb (într-un fişier infix.h), care "exportă" metoda get_tree() (unica "public" explicitată) - aceasta trebuind să returneze obiectul ArTree corespunzător expresiei infixate indicate ca parametru:

#include "arithtree.h"
#include <sstream> // std::istringstream  (operator<<, .str() şi .putback())
#include <string>

class Climb: public ArTree {
public:
    ArTree get_tree(const std::string& expression) { 
        infix.str(expression); // reţine expresia într-un "buffer" intern, de lucru
        return parse_climb(1); // returnează obiectul ArTree corespunzător expresiei
    }    

private:
    std::istringstream infix; // "buffer" pentru expresia dată
    
    ArTree parse_climb(int); // metoda "precedence climbing"
    ArTree parse_primary();

    char look_ahead() { // caracterul următor (fără a avansa în buffer)
        char c; infix >> c; 
        infix.putback(c); // reînscrie caracterul citit, în buffer-ul expresiei
        return c;
    }
};

De exemplu, secvenţa Climb Q; ArTree T = Q.get_tree(" 2 + 3* 4 "); va furniza obiectul ArTree pentru expresia 2+3*4; spaţiile existente nu contează - şi nu fiindcă le-am elimina la preluarea expresiei, ci fiindcă operator<< le "sare" în mod implicit.

Avem nevoie desigur, de funcţii care furnizează priorităţile operatorilor şi caracterul de asociere; le constituim tot în fişierul infix.h, declarându-le ca "inline":

inline int priority(char op) { // priorităţi
    switch(op) {
        case '+': case '-': return 1;
        case '*': case '/': return 2;
        case '^': return 3;
    }
    return 0;
}
inline bool right_ass(char op) { return op == '^'; } // asociere la dreapta

Metodele "private" parse_climb() (apelată direct din get_tree()) şi parse_primary() - pe care le dezvoltăm în fişierul infix.cpp - modelează împreună metoda de analiză precedence climbing, folosind metoda look_ahead() şi funcţiile definite inline mai sus, priority() şi right_ass():

#include "infix.h"
ArTree Climb::parse_climb(int level) {
    ArTree tree = parse_primary(); // operandul curent
    while(priority(look_ahead()) >= level) { // când urmează operator prioritar
        char op; infix >> op;
        // pentru asociere-stânga, măreşte prioritatea curentă
        int next_level = right_ass(op)? priority(op): priority(op) + 1;
        // reapelează parse_climb(), pentru a constitui subarborele drept
        tree = ArTree(op, tree, parse_climb(next_level)); 
    }
    return tree;
}

Am ilustrat deja logica acestei metode, în cursul exemplificărilor precedente (legate de "parse()"). parse_primary() trebuie să se ocupe nu numai de operanzi propriu-zişi (dacă ar fi fost aşa, puteam şi renunţa la aceasta), dar şi de subexpresii parantezate - caz în care apelează parse_climb(1) pentru subexpresia respectivă (fireşte, aceste două metode sunt mutual dependente):

ArTree Climb::parse_primary() {
    char c; infix >> c; // ar trebui să fie sau '(', sau o cifră
    switch(c) {
        case '(': // începe o subexpresie parantezată
            {
              ArTree tree = parse_climb(1); // analizează subexpresia
              
              char p; infix >> p; // sare peste ')' (final subexpresie)
              if(p != ')') throw "Error: paranteze nebalansate";
              
              return tree; // sub-arborele subexpresiei parantezate
            }
        default: // operand numeric (prima cifră a sa)
            {
              if(!(c>='0' && c <='9')) throw "Error: operand nenumeric";
              
              infix.putback(c); // reînscrie cifra şi citeşte numărul
              double number; infix >> number;
              
              return ArTree(number); // construieşte "Operand" şi-l returnează
            }
    }
}

parse_primary() este eventual şi cadrul în care se pot trata diverse erori de sintaxă - dar aici avem o tratare parţială (pentru "paranteze nebalansate" şi pentru "operand nenumeric"); de exemplu, nu am tratat depistarea sfârşitului expresiei: 2*(3-4)^(5-6))*7ab va putea fi tratată ca 2*(3-4)^(5-6).

Rezultatul…

O manieră "decentă" de folosire implică o construcţie try - catch (fără de care, eventualele erori lansate ca mai sus prin throw nu vor fi tratate cum am intenţionat):

vb@vb:~$ ./ast "6 / (1 - 3/4)"
/ 6 - 1 / 3 4 prefix (0)  
(6 / (1 - (3 / 4))) infix (1)
6 1 3 4 / - / postfix (2)
24 valoarea expresiei

vb@vb:~$ ./ast "6 /\ (1 - 3/4)"
Error: operand nenumeric

vb@vb:~$ ./ast "6 /2 (1 - 3/4)"
0: / 6 2 restul este incorect!
1: (6 / 2) 
2: 6 2 / 
3

// g++ --std=gnu++0x -o ast  infix_main.cpp infix.cpp arithtree.cpp
#include "infix.h"
#include <iostream>
int main(int argc, char** argv) {
    Climb infix;
    try {
        ArTree T = infix.get_tree(argv[1]);
        for(int i=0; i < 3; ++i) {
            ArTree::set_format(i);
            std::cout << i << ": " << T << '\n';
        }
        std::cout << T.eval() << '\n';
    } catch(const char* error) {
        std::cout << error << '\n';
    }
}

Rezultatul - afişarea în anumite formate, a unei expresii - este banal (cum şi anticipasem, de la bun început) şi se putea obţine şi direct (fără clasele ArTree şi Climb de aici - instrumentând în schimb un algoritm shunting yard); dar nu rezultatul ca atare ne-a interesat (şi spre deosebire de [2], nu vedem alte aplicaţii semnificative), ci procedeul de analiză bazat pe proprietăţile operatorilor ("precedence climbing" - metodă ingenioasă, compactă şi eficientă de analiză sintactică) - împreună desigur, cu modelarea în C++ a acestuia (plecând de la modelul de arbori aritmetici ArTree).