În studiul obişnuit ("manual") al unei funcţii elementare folosim elemente de "calculul diferenţial"; practic, sintetizăm lucrurile într-un "tabel de variaţie" (reflectând domeniul de definiţie, semnul derivatei şi deducerile de monotonie corespunzătoare, etc.), care ne serveşte apoi pentru a schiţa graficul funcţiei pe întregul domeniu de definiţie.

Modelarea procedeului "teoretic" ar implica metode pentru determinarea domeniului de definiţie, a derivatei şi a rădăcinilor acesteia, a limitelor şi asimptotelor şi eventual, o metodă care să printeze "tabelul de variaţie" final, urmând apoi să-l "transformăm" în graficul propriu-zis al funcţiei date.

Dar este şi necesar să facem "ca la matematică"? Majoritatea programelor procedează pur şi simplu direct (fără nicio "teorie"), conducând la grafice suficient de "corecte" - mizând pe ceea ce nouă ne lipseşte (şi suplinim prin instrumentele teoretice de "analiză matematică"): posibilităţile uriaşe de calcul "brut" şi de reflectare dinamică a calculelor, oferite de calculator.

Anume, dată funcţia f şi capetele unui interval din domeniul ei de definiţie - se consideră o divizare Δ (cât vrem de fină) a acestui interval şi se calculează valorile funcţiei pe nodurile acestei divizări; apoi se parcurge Δ şi se plotează punctele (x∈Δ, y = f(x)).

Problemele trasării graficului

Avem de reprezentat grafic o funcţie elementară (continuă şi derivabilă pe tot domeniul definiţiei). Teoretic, graficul funcţiei este mulţimea punctelor (x, f(x)), x parcurgând (continuu) domeniul de definiţie; această mulţime este infinită, dar ideea programului este de a determina şi a plota un număr rezonabil de mare, de puncte ale graficului - rezultând o aproximaţie a graficului propriu-zis, care se va putea îmbunătăţi mărind numărul de puncte.

Graficul "real" vizează întregul domeniu de definiţie, având eventual mai multe "ramuri" (separate fie prin asimptote verticale, fie prin intervale pe care funcţia nu este definită); dar în program avem de evitat punctele x pentru care "nu se poate calcula" valoarea f(x) - astfel încât trebuie să pretindem ca parametri capetele unui interval aflat (în întregime) în domeniul de definiţie şi vom obţine graficul (aproximativ) pe acest interval, nu dintrodată pe întregul domeniu de definiţie.

Problema principală derivă din modelarea internă a "pânzei" pe care se desenează. Şi pe hârtie şi în cazul unei ferestre din memoria-ecran, desenul "curge" de sus în jos şi de la stânga la dreapta; altfel spus, fiecare punct sau "pixel" este identificat sau adresat prin distanţa la marginea stângă a "pânzei" (ca "abscisă") şi distanţa la marginea de sus (ca "ordonată") - cu valori între zero şi lăţimea/înălţimea fixate ale "pânzei".

Pentru a mapa biunivoc un interval numeric `[S_0, S_1]` obişnuit, pe un domeniu de reprezentare grafică `[T_0, T_1]` putem folosi o funcţie liniară T`(S; S_0, S_1; T_0, T_1) = alpha S + beta` satisfăcând condiţiile T`(S_0) = T_0` şi T`(S_1) = T_1` - ceea ce conduce la această funcţie generală "de scalare":

function scale(s, S0, S1, T0, T1) { // s ∈ [S0, S1]
    return (T1 - T0)/(S1 - S0) * (s - S0) + T0;
}

Astfel, punctul "teoretic" `(X, Y) in [A, B]xx[C, D]` va fi reprezentat prin pixelul care are distanţa la marginea stângă T`(X; A, B; 0, W)` şi are distanţa la marginea de sus egală cu `H - `T`(Y; C, D; 0, H)`, unde `W` este lăţimea şi `H` este înălţimea "pânzei".

Pentru a scala pe verticală va fi necesar calculul prealabil al valorilor funcţiei în punctele divizării Δ considerate - pentru a determina intervalul valorilor lui Y, [C="minim", D="maxim"].

Pe de altă parte, ar trebui să asigurăm o aceeaşi unitate de scalare - iar pentru aceasta, cel mai simplu ar fi să redefinim dimensiunile "pânzei", alegând W = (B - A)*FS şi H = (D - C)*FS, unde FS este un (acelaşi) factor de scalare convenabil. Într-adevăr, conform definiţiei de mai sus am avea imediat T`(X; A, B; 0, W) = W/(B-A)(X-A) = `FS`*(X-A)` şi la fel T`(Y; C, D; 0, H) = `FS`*(Y-C)`.

Schema unui document HTML pentru obţinerea graficelor

Următorul fişier HTML enunţă intenţiile de dezvoltare a codului care - având în vedere cele de mai sus - va crea graficele funcţiilor:

<!DOCTYPE html>
<head><!-- "include" jQuery şi fişierul care defineşte Grafic() --></head>
<body> 
<div id="wrapp">
    <span style="color:red">sin x</span>
    <span style="color:navy">2 cos x + sin x</span>
    <span style="font-size:0.8em">x&in;[-pi, 2 pi + 1], step = 0.01</span>
    <br> <!-- aici va fi adăugat <canvas>-ul graficelor -->
</div>

<script>
function func(x) {
    return 2*Math.cos(x) + Math.sin(x);
}
$(function(){
    var graf = new Grafic([Math.sin, func], [-Math.PI, 2*Math.PI+1], 0.01, 'wrapp');
    // graf.to_canvas();      
});
</script>
</body>

Constructorul Grafic() primeşte ca parametri un tablou cu referinţe la funcţiile de reprezentat, un interval din domeniul comun de definiţie, o valoare numerică mică servind pentru determinarea consecutivă a punctelor pe care să se calculeze valorile funcţiilor, precum şi identificatorul HTML al diviziunii în care să fie adăugat elementul <canvas> care va conţine în final, graficele funcţiilor.

Pe imaginea finală (asociată fişierului HTML redat mai sus) se poate anticipa, cam cum am rezolvat diversele probleme care s-au pus:

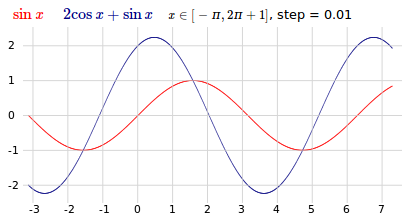
Se vede aici că avem "aceeaşi unitate" şi pe orizontală şi pe verticală; în loc de obişnuitele axe Ox şi Oy am preferat un "grid", marcând dedesubt punctele întregi din intervalul de definiţie şi la stânga - punctele întregi din domeniul maxim al valorilor funcţiilor.

Constructorul Grafic()

Reprezentarea grafică va rezulta prin instanţierea (cu new()) următorului obiect javaScript, care sintetizează parametrii şi metodele necesare:

function Grafic(func, dom_def, step, id_dest) {
    this.func = func; // tablou de referinţe la funcţii: [Math.sin, myFunc1, myFunc2]
    this.step = step; // 0.01 (calculează valorile din sutime în sutime)
    this.def = dom_def; // tablou cu capetele intervalului: [a, b]
    this.y = this.values(); // tablouri de valori ale funcţiilor; this.ymin şi this.ymax

    this.create_canvas(id_dest); // alege un factor comun de scalare şi creează <canvas>
    this.to_canvas(); // reprezentarea grafică propriu-zisă, pe <canvas>
}

Următoarea metodă constituie tabloul this.y=[ [...], [...], ...] conţinând pentru fiecare funcţie indicată în this.func, tabloul valorilor acesteia (pe intervalul this.def, divizat din "step" în "step"):

Grafic.prototype.values = function() {
    var func = this.func, n = func.length,
        a = this.def[0], b = this.def[1], step = this.step;
    var y = [], m = [], M = [];     
    for(var i=0; i < n; i++) { // pentru fiecare funcţie din func[]
        var x = a, fy = [];
        while(x <= b) { // valorile funcţiei curente, din "step" în "step"
            fy.push(func[i](x));
            x += step;
        }
        y.push(fy); // reţine tabloul valorilor funcţiei curente
        m.push(Utils.min_from(fy)); // reţine minimul şi maximul, pentru funcţia curentă
        M.push(Utils.max_from(fy));
    }
    this.ymin = Utils.min_from(m); // minimul şi maximul tuturor valorilor funcţiilor
    this.ymax = Utils.max_from(M);
    return y;
}

Utils() este un pachet de "funcţii utilitare" (vezi "Construim o histogramă"), conţinând min_from() şi max_from() (apelate deja mai sus) şi metoda scale().

Crearea <canvas>-ului

Odată determinate tablourile din this.func[] cu valorile funcţiilor, precum şi valorile this.ymin şi this.ymax - totul este pregătit pentru realizarea reprezentării grafice dorite. Izolăm însă crearea elementului <canvas> de reprezentarea grafică propriu-zisă, pentru eventualitatea punerii la punct a unui procedeu de alegere a factorului de scalare (acelaşi pe ambele axe) şi a dimensiunilor <canvas>-ului în corelaţie cu mărimea valorilor funcţiilor şi a intervalului de definiţie.

Deocamdată să folosim cea mai directă metodă de creare a <canvas>-ului necesar:

Grafic.prototype.create_canvas = function(id_dest) {
    var FS = 35; // un "factor de scalare" comun celor două axe
    this.canvas = document.createElement('canvas');
    this.canvas.setAttribute('width', (this.def[1]-this.def[0])*FS + 30);
    this.canvas.setAttribute('height', (this.ymax-this.ymin)*FS + 30);
    var dest = document.getElementById(id_dest);
    dest.appendChild(this.canvas);
}

Am rezervat pe lăţime şi pe înălţime câte 30 pixeli, intenţionând să trasăm graficele în interiorul <canvas>-ului, lăsând o margine stângă şi una dreaptă, respectiv una sus şi una jos (aceste margini vor servi pentru marcarea absciselor şi ordonatelor de ghidare).

Aşa scrisă, create_canvas() nu asigură decât faptul că vom avea "aceeaşi unitate" pe cele două axe; dacă maximul dintre lungimea intervalului this.def şi respectiv, distanţa this.ymax - this.ymin este prea mare - atunci fie lăţimea, fie înălţimea <canvas>-ului creat va fi inconvenabil de mare. Deocamdată, într-un asemenea caz - utilizatorul va putea să reia, micşorând factorul FS, sau îngustând intervalul de definiţie, sau eventual scalând valorile funcţiei (de exemplu, furnizând ca funcţie nu direct "Math.exp", ci definind o funcţie "myExp" care să returneze 0.01*Math.exp(x)).

Trasarea graficelor

Întâi localizăm - pentru accesare internă mai rapidă - variabilele necesare: capetele intervalului de definiţie, tabloul care conţine subtablourile valorilor funcţiilor, valorile "ymin" şi "ymax" şi obiectul "canvas" (creat anterior prin metoda create_canvas()); instanţiem (apelând Utils.colors()) un tabel de culori contrastante - câte una pentru fiecare funcţie - şi fixăm marginile (stânga, dreapta, sus, jos) şi calculăm dimensiunile W, H ale graficului propriu-zis.

Apoi, pentru fiecare funcţie desenăm punctele graficului său: determinăm abscisa curentă "px" şi o scalăm faţă de W, determinăm ordonata "py" (scalată faţă de H, folosind Utils.scale()) şi plotăm la abscisa şi ordonata respectivă - folosind metoda fillRect(), din contextul "2d" al obiectului "canvas" - un pătrăţel de dimensiune foarte mică (0.75 px) - repetând aceste operaţii pentru fecare punct.

În final, trasăm liniile orizontale şi marcăm ordonatele, apoi pe cele verticale, marcând abscisele.

Grafic.prototype.to_canvas = function() {
    var a = this.def[0], b = this.def[1], step = this.step, 
        Y = this.y, N = Y[0].length,
        ymax = this.ymax, ymin = this.ymin;
    var canvas = this.canvas,
        ctx = canvas.getContext("2d"),
        colors = Utils.colors(Y.length);
    var i, j, px, py,
        top = 10, bottom = 20, left = 20, right = 10,
        H = canvas.height - bottom - top,
        W = canvas.width - left - right;
    for(j=0, nf=Y.length; j < nf; j++) {
        ctx.fillStyle = colors[j]; // schimbă culoarea, pentru noua funcţie    
        var y = Y[j];
        for(i=0, px=a; i < N; i++) { // graficul funcţiei curente
           var py = H + top - Utils.scale(y[i], ymin, ymax, 0, H);
           ctx.fillRect(left + Utils.scale(px, a, b, 0, W), py, 0.75, 0.75);
           px += step;
        }
    }
    ctx.strokeStyle = "rgba(200, 200, 200, 0.75)"; // pentru grid
    ctx.font = 'normal 8pt monospaced'; // pentru marcarea coordonatelor
    ctx.fillStyle = "black";
    var sy = Math.ceil(ymax - ymin);
    for(i=-sy+1; i < sy; i++) { // orizontalele grid-ului
        py = H + top - Utils.scale(i, ymin, ymax, 0, H);
        ctx.moveTo(15, py+0.5); 
        ctx.lineTo(W + left + right, py+0.5);
        ctx.fillText(i, 0, py+4); // marchează ordonatele 
    }
    var sx = Math.ceil(b-a);
    for(i=-sx+1; i < sx; i++) { // verticalele grid-ului
        px = left + Utils.scale(i, a, b, 0, W);
        ctx.moveTo(px, H + bottom); 
        ctx.lineTo(px, 0);
        ctx.fillText(i, px-4, H + top + bottom); // marchează abscisele
    }
    ctx.stroke();
}

Desigur, reprezentarea "prin puncte" (folosind fillRect()) are defectele ei; dacă "step"-ul ales este de ordinul zecimilor (adică, prea mare), sau dacă valorile uneia dintre funcţiile date cresc foarte repede - atunci "graficul" care va rezulta este format din puncte clar distanţate între ele. Alternativa (foarte obişnuită) constă în poziţionarea iniţială a trasării în primul punct al graficului (cu moveTo()) şi apoi trasarea unei "linii" de la punctul curent către cel următor (folosind lineTo()).

Grila instituită peste grafice (şi marcarea absciselor şi a ordonatelor, folosind fillText() - dar în cel mai simplu mod) poate să fie nepotrivită în unele cazuri, pentru că sunt vizate numai punctele întregi din intervalul de definiţie şi respectiv, din intervalul valorilor funcţiilor; ori uneori este utilă şi o grilă pentru un domeniu ca [0.1, 0.9] ("din zecime în zecime", sau pe multipli de zecimi).