O histogramă este o funcţie care partiţionează un set de date numerice într-un anumit număr de clase şi asociază fiecărei clase o valoare care reflectă numărul de date înregistrate pe acea clasă.

Criteriul de partiţionare depinde de contextul datelor. De exemplu, pentru mediile obţinute de elevi în urma unui examen - ne-ar interesa repartizarea mediilor între anumite valori; pentru o imagine digitală - tot "un set de date numerice", reprezentând culorile pixelilor - poate fi relevantă proporţia sau densitatea fiecărei culori în cadrul imaginii (histograma servind apoi pentru retuşarea imaginii).

Pentru realizarea histogramelor se pot folosi după caz, Microsoft Excel, GNU gnumeric, Google Spreadsheet, sau procesoare de imagine precum GIMP; pachete ca matplotlib sau OpenCV; diverse applet-uri Java (www.shodor.org, nlvm.usu.edu); biblioteci javaScript precum jqplot, Raphael, etc.

Aici vom aborda metodic (iarăşi - ca un exerciţiu de elaborare a unei aplicaţii) construcţia unei histograme folosind elementele unui browser (javaScript, <canvas>).

Un pachet de funcţii utilitare

Sunt de prevăzut întâi, câteva funcţii generice: vom avea de calculat suma numerelor dintr-un tablou sau altul, de iniţializat un tablou cu anumite valori, de aflat minimul sau maximul dintr-un Array(), etc. Prevăzându-le ca o entitate separată, vom putea să le punem la punct - să le testăm, să le rescriem - mai uşor şi vom putea refolosi "biblioteca" respectivă în alte aplicaţii.

În fond, chiar javaScript oferă asemenea "pachete de funcţii utilitare" - de exemplu, Math grupează şi modelează diverse funcţii matematice, accesibile din propriul cod prin "operatorul punct"; astfel, Math.max(1,2,3,4) furnizează valoarea maximă dintr-o listă obişnuită (nu array) de numere.

Putem defini astfel un obiect ("dicţionar" de funcţii) conţinând funcţiile de care vom avea nevoie:

var Utils = {

    init_array: function (len, val) {
        // returnează un "array" cu lungimea şi valoarea iniţială date
    },

    sum: function(array) {
        // returnează suma numerelor din "array"
    }
    
    // alte componente ale obiectului "Utils", separate prin virgulă

};

Fiindcă vor fi de parcurs elementele unui "array" (şi de exemplu, histograma unei imagini digitale implică "array" de sute de mii de pixeli) - ar fi de avut în vedere unele "trucuri" de optimizare a codului (google javascript optimization techniques):

1
2
3
4
5
6
7
8
9

var Utils = {
    init_array: function (len, val) {
        var array = [val];
        while(--len)
            array[len] = val;
        return array;
    }
    //, 
};

var myArr = Utils.init_array(1000, 5.3);
alert(myArr[123]);

În cazul parcurgerii obişnuite for(var k=0; k < len; k++) {...}, la fiecare iteraţie s-ar evalua condiţia "k < len" şi apoi s-ar incrementa contorul (repetând blocul de calcul dacă testul dă "true"); în schimb, while(--len) {...} este mult mai rapid, fiindcă - fără să mai fie nevoie de o variabilă suplimentară - decrementează "len" şi totodată testează dacă s-a ajuns la zero (când "se iese" din ciclu).

De fapt, un tablou iniţializat cu o anumită valoare poate fi obţinut şi "direct", îmbinând metode existente în obiectele predefinite Array() şi String() - cum se vede pe acest exemplu:

var arr = new Array(4); // Tablou cu 4 elemente, nedefinite: arr=[,,,]
                        // (alert(arr) afişează virgulă între elementele consecutive)

var str = myArr.join('5.3,'); // Alipeşte cele 4 elemente (şiruri vide), intercalând 
                              // între oricare două şirul "5.3," - rezultând un şir în
                              // care se repetă "5.3," de 3 ori: str="5.3,5.3,5.3"

var myArr = str.split(','); // Desparte şirul la "," rezultând un tablou cu 3 elemente,
                            // egale toate cu şirul "5.3": myArr = ["5.33", "5.33", "5.33"] 

În final obţinem un tablou de şiruri, iar aici vom avea de lucrat cu valori numerice; în acest caz este de preferat funcţia init_array() concepută mai sus.

Ideea tocmai ilustrată este adecvată în alt scop. Vom dori să redăm o histogramă şi în formă textuală, reprezentând o clasă de valori de exemplu printr-un şir de caractere "*" (de lungime proporţională cu volumul acelei clase) - iar pentru o funcţie care să producă un astfel de şir putem "înlănţui" ca şi mai sus, constructorul Array() şi metoda join():

var Utils = {
    /* ... */
    rep_str: function(str, n) {
        return Array(n+1).join(str);
    }
};

Astfel, apelul Utils.rep_str('*', 4) va returna şirul "****".

Scalarea liniară a valorilor

Vom dori să redăm histograma şi în mod grafic - reprezentându-i clasele prin dreptunghiuri alăturate orizontal într-o fereastră de ecran, având fiecare o anumită lăţime şi cu înălţimea proporţională cu numărul de valori înregistrate în clasa respectivă.

Ar fi două posibilităţi pentru vizualizarea dreptunghiurilor: fie implicăm elemente <div> pentru care setăm "float: left" pentru alăturare pe orizontală şi apoi "width" şi "height" corespunzător lăţimii şi înălţimii (şi desigur, "background" sau "border") - fie folosim un element <canvas> şi metodele aferente acestuia.

În oricare caz, va fi nevoie de o "măsură în pixeli" care să păstreze proporţiile, pentru valorile date. Am avea de stabilit o funcţie liniară F: [S₀, S₁] −> [T₀, T₁], F(v) = α*v + β care să exprime în pixeli (între T₀ pixeli şi cel mult T₁ pixeli) o valoare obişnuită v.

Determinăm parametrii α şi β rezolvând condiţiile F(S₀) = T₀, F(S₁) = T₁ şi putem formula:

var Utils = {
    /* ... */
    scale: function(Val, s0, s1, t0, t1) {
        return (t1-t0)/(s1-s0)*(Val-s0) + t0;
    }
};

De exemplu, dacă valorile date sunt cuprinse în intervalul [a, b] şi vrem să le repartizăm în N clase echidistante, atunci "lăţimea" fiecărui subinterval va fi Δ = (b - a)/N iar lăţimea dreptunghiului corespunzător pe ecran va fi Δ_px = Utils.scale(Δ, 0, b-a, 0, W), unde W este valoarea proprietăţii "width" a <div>-iziunii destinate redării grafice a histogramei.

Ne putem aştepta la unele probleme de rotunjire (cu javaScript) a rezultatelor unor asemenea calcule; deocamdată putem ignora acest aspect.

Schema unui document HTML pentru obţinerea histogramei

Înscriem Utils() - care conţine "funcţii utilitare" precum cele descrise mai sus - în fişierul "utils.js" şi creem un fişier "histogram.js" în care urmează să constituim codul pentru realizarea histogramei. Următorul fişier HTML enunţă intenţiile de dezvoltare a codului histogramei:

<!DOCTYPE html>
<head>
    <meta charset="utf-8">
    <title>Histogram</title>
<script src="http://ajax.googleapis.com/ajax/libs/jquery/1.9.1/jquery.min.js"></script>
    <script src="utils.js"></script>
    <script src="histogram.js"></script>
</head>
<body> 
    <div id="hist-info" style="font-size:0.9em;"></div>
    <div id="hist-string" style="font-family:monospace"></div>
    <div id="hist-canvas"></div>
<script>
    $(function(){
        var probe = [4.37,3.87,4.00,4.03,3.50,4.08,2.25,4.70,1.73,4.93,1.73,4.62
            /* , ... */ ];
        var histogram = new Histogram(probe, 12);
        $('#hist-info').html(histogram.info());
        histogram.to_string('hist-string');
        histogram.to_canvas('hist-canvas', {'width': 400, 'height':250});
    });
</script>
</body>

Este deja banal, că am inclus jQuery - simplificând accesarea din cod javaScript a obiectelor documentului; de exemplu putem folosi $('#id') în loc de document.getElementById('id'), sau $('#id').html(cod_html) în loc de document.getElementById('id').innerHTML = cod_html. La fel - ambalarea într-o construcţie finală $(function(){...}) a codului care va trebui executat de către browser după ce va constitui în memorie arborele obiectelor documentului ("DOM"-ul).

În <script>-ul din finalul fişierului - Histogram(probe, 12) va trebui să partiţioneze tabloul "probe" într-un număr de 12 clase de valori, punând la dispoziţie metodele this.info(), this.to_string() şi this.to_canvas() unde this referă obiectul construit de Histogram() (indicat în cazul de faţă prin variabila "histogram").

Şirul HTML returnat de histogram.info() (şi înscris ca atare în diviziunea identificată prin "hist-info") va conţine informaţii precum: numărul de date, valoarea medie, dispersia, numărul de clase.

histogram.to_string() va înscrie în diviziunea indicată formatul-text al histogramei, iar to_canvas() va crea şi va înscrie în diviziunea indicată un element <canvas> conţinând formatul-grafic.

Desigur, după ce vom fi pus la punct aceste intenţii, vom putea dori mai mult decât preconizează fişierul HTML considerat mai sus; de exemplu - datele să fie preluate direct de la utilizator (prin intermediul unui element <textarea>), iar rezultatele să fie redate fără să fie necesară invocarea explicită a metodelor indicate mai sus.

Constructorul histogramei

Vrem să partiţionăm în intervale (denumite "bin", adică "dulap") de o aceeaşi lungime Δ - deci Δ = (_max - _min) / _clase, unde _clase este numărul dorit de "bin"-uri, iar _max şi _min sunt valoarea cea mai mare şi respectiv cea mai mică, dintre valorile numerice date.

Primul "bin" va trebui să înregistreze valorile cuprinse între _min şi _min + Δ şi această regulă ar rămâne valabilă pentru toate "bin"-urile, dacă de fiecare dată am exclude valorile deja înregistrate şi am determina _min dintre valorile rămase. Putem însă evita marcările "deja înregistrat" şi găsirea repetată a _min dintre valorile neînregistrate - ordonând în prealabil valorile date; nu-i neapărat "cel mai bine", dar aici aşa vom proceda: ordonăm din start în sens crescător, tabloul valorilor date (încât _min şi _max sunt respectiv prima şi ultima valoare din acest tablou).

Să observăm însă că nu este vorba de "partiţionare" propriu-zisă şi nici de "înregistrarea valorilor cuprinse între"; nu ne interesează să colectăm în "bin"-uri valorile ca atare - ci să reţinem numărul acestor valori (sau proporţia acestora, în cadrul setului dat). Prevedem metoda _bin_range() care să determine câte valori corespund fiecărui "bin", păstrând rezultatele în tabloul intern this.bins[]; iar this.ranges[] va păstra limita superioară pentru fiecare "bin".

function Histogram(data, n_clase) {
    this.samples = data.sort(function(a, b) {return a-b;});
    this.n_bins = n_clase || this.number_of_bins();   
    this.bins = Utils.init_array(this.n_bins, 0); 
    this.ranges = Utils.init_array(this.n_bins + 1, 0);
    this._bin_range();
}

Dacă utilizatorul nu specifică şi parametrul "n_clase" (numărul de "bin"-uri), atunci constructorul redat mai sus apelează metoda _number_of_bins():

Histogram.prototype.number_of_bins = function() {
    return 12;
    // return Math.ceil(1 + Math.log(this.samples.length)/Math.LN2); // (formula lui Sturges)
    // return Math.ceil(Math.sqrt(this.samples.length)); // (folosită de Excel)
    // - a vedea http://en.wikipedia.org/wiki/Histogram pentru alte formule
}

Dacă numărul de "bin"-uri este prea mic, atunci histograma nu va putea reflecta "corect" distribuţia datelor; iar dacă este prea mare - ea va conţine prea multe fluctuaţii ("amănunte"), îngreunând caracterizarea sintetică a distribuţiei valorilor respective.

Construcţia histogramei este finalizată apelând metoda:

Histogram.prototype._bin_range = function() { 
    var sample = this.samples, bins = this.bins, ranges = this.ranges;
    var np = sample.length, nb = this.n_bins, 
        _min = sample[0], _max = sample[np-1];
    var delta = this.delta = (_max - _min) / nb; // Δ va servi pentru scalări
    var i = 0, j = 0,  // bin[i] = numărul valorilor din sample[]
        _vr = ranges[0] = _min; // cuprinse între _vr şi _vr + Δ (pentru _vr curent)
    while(j < np && i < nb) { 
        _vr += delta;
        ranges[i+1] = Math.round(_vr*100)/100; // "limita superioară" a "bin"-ului
        while(sample[j] <= _vr && j < np) {
            bins[i]++; // contorizează valorile corespunzătoare "bin"-ului
            j++;
        }
        i++; // "bin"-ul următor
    }
}

Logica acestei metode este destul de banală: tabloul valorilor fiind deja ordonat crescător, se consideră o variabilă _vr cu valoarea iniţială _min şi se traversează tabloul - contorizând în "bin"-ul curent - cât timp valoarea curent întâlnită este mai mică decât vr + Δ; când se întâlneşte prima valoare mai mare decât această limită - se măreşte _vr cu Δ şi se continuă traversarea menţionată, de data aceasta contorizând în contul următorului "bin".

Dar această "simplitate" este oarecum înşelătoare. Pentru cazul unor valori neîntregi apropiate între ele, este posibil ca unele dintre aceste valori să fie "sărite" (compararea unor valori în "virgulă mobilă" necesitând de regulă precauţii care aici lipsesc); astfel, într-un experiment cu metoda enunţată mai sus, numărul de valori (de genul 4.38) a fost 428, în timp ce suma contorilor bin[] a fost 424 - adică au fost "scăpate" 4 valori (neglijabil totuşi, într-un studiu statistic).

Reprezentarea textuală a histogramei

Următoarea metodă creează un element <table> - pe care îl va insera în diviziunea indicată - în care fiecare rând reprezintă un "bin" prin: numărul de valori şi limitele încadrării acestora, proporţia lor în cadrul întregului set de date şi un şir de "*" a cărui lungime corespunde acestei proporţii.

Histogram.prototype.to_string = function(id_div) {
    var dom = $('#' + id_div);
    var table = ['<table>'];
    var bins = this.bins,
        ranges = this.ranges,
        N = this.samples.length,
        sp = 0; // suma "probabilităţilor" bins[i]/N (ar trebui să fie 1)
    for(var i=0, n=bins.length; i<n; i++) {
        var prob = Math.ceil(bins[i]/N*10000)/100;
        sp += prob;
        var rect = Utils.rep_str('*', Math.round(prob));
        table.push('<tr><td>', bins[i], '&nbsp;&nbsp;</td><td>', 
                   ranges[i], ' - ', ranges[i+1], '&nbsp;&nbsp;</td><td>', 
                   prob,'%&nbsp;&nbsp;</td>');
        table.push('<td>', rect, '</td></tr>');
    }
    table.push('<tr><td style="border-top:1px solid #666;">', Utils.sum(bins), 
               '</td><td align="center" style="border-top:1px solid #666;">', 
               Math.round(this.delta*100)/100, '</td>',
               '<td style="border-top:1px solid #666;">Δ = ', 
               Math.round(sp*100)/100,'%</td><td></td></tr>');
    table.push('</table>');
    dom.html(table.join(''));
}

Precedând tabelul furnizat cu rezultatul apelării metodei:

Histogram.prototype.info = function() {
    this.statistics(); // determină stats={media, dispersia} valorilor
    var hist = [];
    hist.push('<p>', 'probe: ',this.samples.length, 
              '; media: ',this.stats['mean'],
              '; dispersia: ', this.stats['disp'], 
              '; intervale: ', this.n_bins, '</p>');
    return hist.join(''); 
}

avem această exemplificare de reprezentare textuală a histogramei:

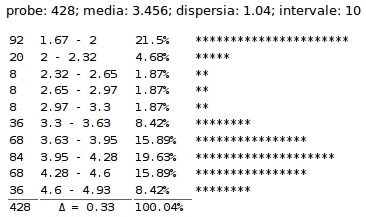
În calculul practic intervin erori de rotunjire, încât este de acceptat să obţinem o valoare suficient de apropiată de 100%, pentru suma "probabilităţilor" din ultima coloană.

Reprezentarea grafică a histogramei

Histograma redată textual mai sus poate fi reprezentată grafic astfel:

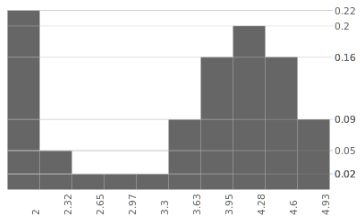
Cotele din dreapta indică înălţimile "bin"-urilor, determinate ca bins[i] / (N*Δ) - astfel că suma ariilor dreptunghiurilor (acestea având lăţimea Δ) este egală teoretic, cu 1 - ceea ce permite eventual (cu Δ potrivit) estimarea "densităţii de probabilitate" (pentru care integrala este 1).

Pentru investigaţiile statistice un scop al histogramei ar fi acela de a estima probabilitatea ca o nouă valoare să "cadă" într-un anumit "bin": s-au colectat date privitoare la accesarea anumitor pagini ale unui site de către diverse categorii de utilizatori şi pe baza histogramei colectate şi prelucrate se evaluează probabilitatea ca (în viitor) un utilizator să ajungă la o anumită pagină.

Metoda următoare creează un element <canvas> (ale cărui dimensiuni pot fi transmise eventual prin parametrul "options") şi îl adaugă în final, în diviziunea indicată. În interiorul acestui <canvas> - lăsând anumite margini, setabile şi acestea prin "options" - se constituie reprezentarea grafică a histogramei, pe baza tablourilor this.bins[] şi this.ranges[] şi a valorii this.delta - rezultate anterior prin apelarea metodei _bin_range() de către constructorul histogramei.

Histogram.prototype.to_canvas = function(id_dest, options) {
    var bins = this.bins, nb = bins.length, N = this.samples.length, 
        dx = this.delta;
    var width = options.width || 500,
        height = options.height || 500,
        top = options.top || 20,
        bottom = options.bottom || 30,
        right = options.right || 40;
    canvas = document.createElement('canvas');
    canvas.setAttribute('width', width);
    canvas.setAttribute('height', height);
    ctx = canvas.getContext("2d");
    ctx.font = 'normal 8pt monospaced';
    ctx.fillStyle = '#666'; 
    ctx.strokeStyle = "rgba(200, 200, 200, 0.15)";

    var h_bins = [], i, px, py;
    for(i=0; i<nb; i++)
        h_bins.push(bins[i]/(N*dx)); // înălţimile "bin"-urilor
    var ymax = Utils.max_from(h_bins),
        H = height - bottom - top,
        W = width - right,
        xmin = this.ranges[0],
        xmax = this.ranges[nb],
        delta = Utils.scale(dx, 0, nb*dx, 0, W); 
    for(i=0, px=0; i<nb; i++) {
        var py = H+top - Utils.scale(h_bins[i], 0, ymax, 0, H);
        ctx.fillRect(px+0.5, py+0.5, delta, H+top - py);
        // scrie înălţimea "bin"-ului, la marginea din dreapta
        if(bins[i]) {
            ctx.moveTo(0, py+0.5);
            ctx.lineTo(W+4, py+0.5);
            ctx.stroke();
            ctx.fillText(Math.ceil(bins[i]/N*100)/100, W+5.5, py + 4.5);
        }
        px += delta;
        // scrie limita din ranges[], la marginea de jos (dar rotind textul cu 90°)
        ctx.save();
        ctx.translate(px, H+top+bottom);
        ctx.rotate(-Math.PI/2);
        ctx.fillText(this.ranges[i+1], 1.5, dx-0.5);
        ctx.restore();
    }
    var dest = document.getElementById(id_dest);
    dest.appendChild(canvas);
}

Cea mai simplă "îmbunătăţire" ţine de gestionarea dicţionarului (cum i-am zice în Python) "options". Metoda nu poate fi apelată prin histogram.to_canvas('id_dest') - eroare: "undefined options" - trebuind neapărat indicat şi "options", eventual vid "{}"; aceasta se poate corecta la o adică, scriind options && options.width || 500 în loc de var width = options.width || 500, etc.

Metodele obiectului "canvas" sunt documentate în numeroase locuri, iar altfel programul redat mai sus nu are nimic deosebit: pentru fiecare "bin" se ridică un dreptunghi folosind metoda fillRect(), cu un vârf în pixelul de coordonate (px, py), de lăţime Δ şi cu înălţimea corespunzătoare "bin"-ului - toţi aceşti parametri având valorile "în pixeli" determinate prin Utils.scale(); totodată, cu fillText() se scriu dedesubt şi la ordonata bazei de sus a dreptunghiului, valorile specifice "bin"-ului respectiv.