1. Provocări prealabile

Folosind aplicaţia din [3], am experimentat cu diverse polinoame (de două variabile) de grad 3, reduse faţă de un anumit modul; de exemplu, pentru (a*b2 + b*a2) % 20:

În javaScript, operatorul "modulo" păstrează semnul deîmpărţitului (de exemplu, (-19) % 5 dă -4); funcţia abs() (vezi eventual codul sursă de la [3]) corectează aceasta, adunând când este cazul, valoarea din "Mod" - astfel încât rezultă indecşi de culoare 0..mod - 1.

Pentru imaginea din dreapta am exclus abs(). Fiindcă originea este luată în centrul pânzei (iar height < width), rezultă că pentru punctele (a, b) din al doilea cadran valorile polinomului sunt negative - încât netrecându-le prin abs(), acestor valori le-ar fi asociată o culoare "undefined", interpretată eventual ca 0 (adică "negru"). Imaginea rezultată astfel evidenţiază ramurile curbei "de bază" a ei, f(x, y) = xy2 + x2y sau simplificând, (x + y)xy.

De altfel, debifând 'Use "anti-alias colors"' obţinem o imagine (prima de mai jos) care sugerează ca "bază" două curbe simetrice faţă de origine (apărute împreună fiindcă acum, am pus funcţia respectivă sub abs()) - fiecare cu câte trei ramuri:

Am mai constatat că adăugarea unor termeni de grad cel mult doi (ca a², a*b, etc.) nu modifică esenţial, imaginea respectivă - exceptând cazuri precum cel reflectat mai sus pe imaginea din dreapta, când îi şi scalăm suficient de mult (de exemplu, cu 100*a*b).

Avem diverse versiuni şi completări (mai "colorate"), folosind funcţia decorate() din [1]:

cub <- function(x, y) abs(x*y*(x + y))
col <- RColorBrewer::brewer.pal(6, "Spectral")  #             
decorate(W=200, FUN=function(u, v) round(cub(u, v) / 1000), col=col, v=73)
# conturează eventual, "curbele de nivel" (panoul din mijloc):
contour(0:400, 0:400, outer(-200:200, 200:-200, 
                            function(u, v) round(cub(u, v) / 50000) %% 73 %% 6), 
        add=TRUE, drawlabels=FALSE, col="dimgray")

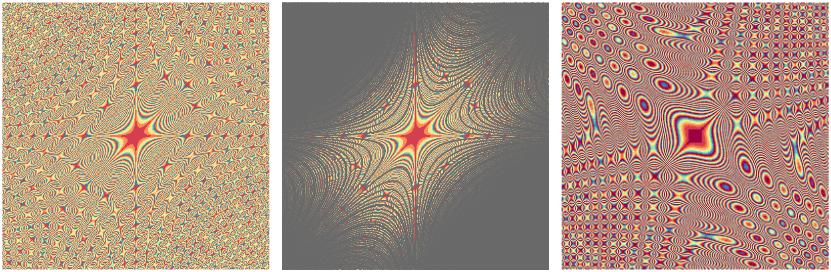
În al treilea panou am angajat sub abs() valorile (x + y)(2x2 - 3xy + 2y2), scalate prin 10^-3 (fiindcă iniţial, "valoarea orientativă" a reducerii stabilite în decorate() era totuşi, prea mare), rotunjite şi reduse apoi % 11, fiind în final colorate % 10. Paleta de culori folosită ("Spectral", din pachetul "RColorBrewer") prevede culori mai închise spre capete şi mai palide în centru; de exemplu pentru prima dintre cele trei imagini, resturile finale (după reducerea modulo 6) 0, 1 şi 5, 4 sunt colorate dinspre roşu, respectiv albastru, iar valorile 2 şi 3 sunt colorate spre gălbui.

Titlul "provocări" nu este chiar gratuit: în [1] şi [2] avem "decoraţiuni", în care - în general - un anumit model grafic se repetă în tot planul - ori în cazul polinoamelor de grad 3, modelul din jurul centrului este irepetabil (şi ar fi de explicat formarea acestuia)…

2. Aproximarea curbelor de nivel

În panoul din mijloc am suprapus imaginii din primul panou, "curbele de nivel" produse pentru datele respective de funcţia contour() (v. ultima comandă din secvenţa redată mai sus). Teoretic, o curbă de nivel pentru funcţia dată f(x, y) conţine toate punctele (x, y) pentru care f(x, y) = L (= constant); dar contour() nu cunoaşte funcţia respectivă, primind ca argument doar un set de valori ale acesteia (şi doi vectori de coordonate pentru punctele în care vrem să fie reliefate valorile respective).

Primind în argumentul "levels" o valoare L, contour() va determina (şi va trasa) "curba de nivel" corespunzătoare folosind un algoritm numeric complicat, din gama Marching_squares; ca idee - se pleacă de la o imagine binară a valorilor (asociind 0 valorilor mai mici decât L şi 1 celorlalte), se identifică apoi fiecare bloc de 2×2 pixeli într-un set de şabloane posibile pentru segmentele de trasat în interiorul unui astfel de bloc şi în final se interpolează faţă de valorile iniţiale, corectând cât mai bine poziţia acestor segmente.

Ilustrăm lucrurile (mai "pe deasupra"), considerând un număr mic de date:

cubic <- function(x, y) x*y*(x+y)
x <- y <- -4:4  # abscise şi ordonate
K <- outer(x, y, cubic)
contour(x, y, K, levels=c(2, 4, 6, -4, -9)) 
> rownames(K) <- colnames(K) <- -4:4
> K
     -4  -3  -2  -1 0  1  2  3   4
-4 -128 -84 -48 -20 0 12 16 12   0
-3  -84 -54 -30 -12 0  6  6  0 -12
-2  -48 -30 -16  -6 0  2  0 -6 -16
-1  -20 -12  -6  -2 0  0 -2 -6 -12
0     0   0   0   0 0  0  0  0   0
1    12   6   2   0 0  2  6 12  20
2    16   6   0  -2 0  6 16 30  48
3    12   0  -6  -6 0 12 30 54  84
4     0 -12 -16 -12 0 20 48 84 128

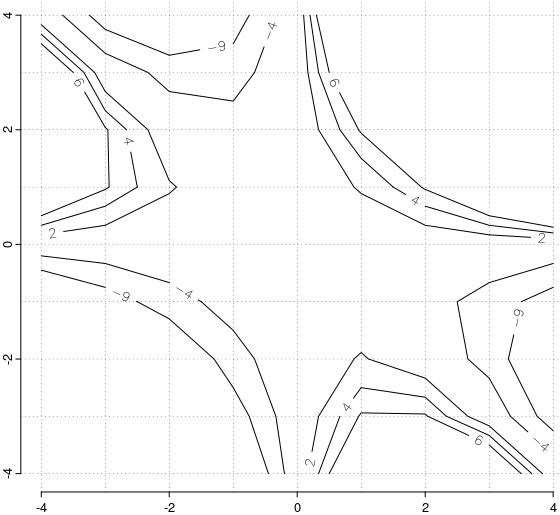
Matricea K conţine valorile funcţiei cubic(), pentru abscisele şi ordonatele indicate în vectorii x şi y; după redenumirea liniilor şi coloanelor avem de exemplu, K["-2", "1"] = 2 (= cubic(-2, 1)) - şi pe graficul alăturat se vede că punctul (-2, 1) este foarte aproape de ramura din al doilea cadran al curbei de nivel marcate cu "2" (care are trei ramuri - în primul, al doilea şi al patrulea cadran).

Să observăm că în K nu apare valoarea 4; să facem o mică verificare: vedem pe grafic că ramura din al patrulea cadran a curbei de nivel 4 trece puţin mai jos de punctul (1, -2.5), iar calculul direct ne dă cubic(1, -2.5) = 3.75 ("aproape" de 4); coborând puţin, avem cubic(1, -2.6) = 4.16 şi interpolând între aceste valori avem 3.955, ajungând "foarte aproape" de nivelul 4. Sondând în acest mod, ne putem încredinţa că într-adevăr, cele câte trei contururi segmentate la fel marcate constituie împreună aproximări acceptabile ale curbelor de nivel aferente etichetelor respective.

Desigur, putem obţine curbe de nivel mai "netede" - înscriind în matricea K un număr mai mare de valori ale funcţiei:

x <- y <- seq(-12, 12, length=240)  # 240×240 puncte (din pătratul [-12,12]×[-12,12])
K <- outer(x, y, cubic)  # valorile funcţiei 'cubic' în punctele reţelei
plot.new()
contour(x, y, K, levels=0, col="black", lwd=0.5, lty="dashed", labcex=0.9)
contour(x, y, K, levels=c(5, 10, 20), col=c('red', "darkgreen", "blue"), 
        lwd=0.9, labcex=0.9, add=TRUE)
contour(x, y, K, levels=10*-20:-1, drawlabels=FALSE, col="lightpink4", 
        lty="dotted", add=TRUE)

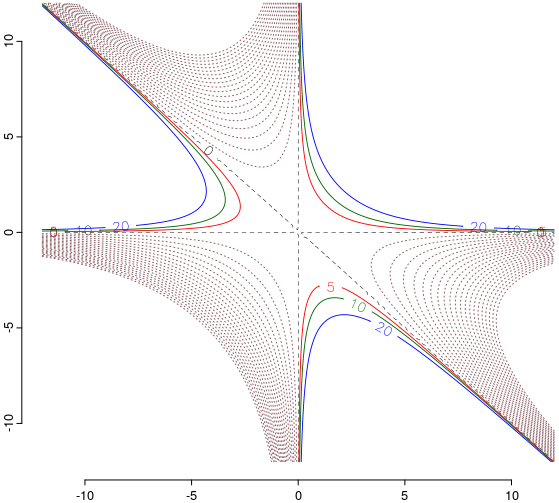
Am conturat întâi curba de nivel 0; teoretic, aceasta este formată din punctele axelor şi cele ale bisectoarei a doua (fiindcă xy(x+y)=0 implică x=0, sau y=0, sau x=-y). Apoi am conturat trei curbe de nivel pozitiv (5, 10 şi 20) şi în final, 20 de linii punctate, de nivele negative.

Forma polară şi graficul cubicei de ecuaţie implicită xy(x+y)=λ

Cele trei ramuri colorate cu roşu din imaginea rezultată mai sus prin contour(), constituie în fond o reprezentare suficient de bună a graficului funcţiei implicite cubic(x, y) = 5. Totuşi - cum am programa direct, plotarea curbei Γ ≡ Γ_λ de ecuaţie xy(x + y) = λ (constant)?

Desigur, putem face în prealabil unele observaţii directe: dacă (x, y) ∈ Γ atunci (y, x) ∈ Γ - adică Γ este simetrică faţă de prima bisectoare (pe care o şi intersectează, în punctul x = y = (λ/2)^1/3). Putem exclude cazul banal λ = 0, când Γ "degenerează" în reuniunea a trei drepte: cele două axe şi a doua bisectoare a sistemului de axe.

Dacă (x, y) ∈ Γ atunci x şi y trebuie să aibă sau semne contrare, sau acelaşi semn cu λ (de exemplu, dacă λ > 0 şi x < 0 atunci nu putem avea y < 0 fiindcă ar rezulta xy(x + y) < 0 < λ). Rezultă că Γ nu are puncte în cadranul opus celui în care coordonatele au acelaşi semn cu λ.

Un calcul simplu ne poate arăta că există o vecinătate a originii în care Γ nu are puncte; de exemplu, considerând ecuaţia curbei ca ecuaţie de gradul doi în variabila x (analog, în variabila y), avem Δ = y(y³ + 4λ) şi avem Δ > 0 (deci putem determina x) numai pentru valorile y dinafara intervalului de capete 0 şi rădăcina cubică a valorii (-4λ).

Să mai observăm că Γ_λ şi Γ_-λ sunt simetrice una celeilate atât faţă de originea axelor, cât şi faţă de a doua bisectoare (fiindcă (x, y) ∈ Γ_λ implică (-x, -y) ∈ Γ_-λ şi (-y, -x) ∈ Γ_-λ).

În vederea regizării reprezentării grafice, putem încerca să parametrizăm ecuaţia iniţială - dată în formă implicită - a curbei Γ. Fie x = ρ cos(θ) şi y = ρ sin(θ), cu ρ > 0 şi θ ∈ [0, 2π); un calcul relativ simplu transformă ecuaţia iniţială în "forma polară": ρ3 = 20.5λ / (sin(2θ) sin(θ + π/4)) - iar aceasta se poate "programa" relativ uşor:

sqrt3 <- function(x) {  # rădăcina cubică (inclusiv, din valori negative)
  sign(x) * abs(x) ^ (1/3)
}  # (-8) ^ (1/3) are ca rezultat "NaN"; sqrt3(-8) dă -2

# setează panoul grafic şi trasează axele şi a doua bisectoare
plot(0, 0, type="n", xlim=c(-15, 15), ylim=c(-15, 15), xlab="", ylab="", bty="n", 
     cex.axis=0.8, mgp=c(3, 0.25, 0), cex.lab=0.6, tcl=NA)
abline(v=0, h=0, lwd=0.3, col="dimgray", lty="dashed")
abline(0, -1, lwd=0.3, col="dimgray", lty="dashed")

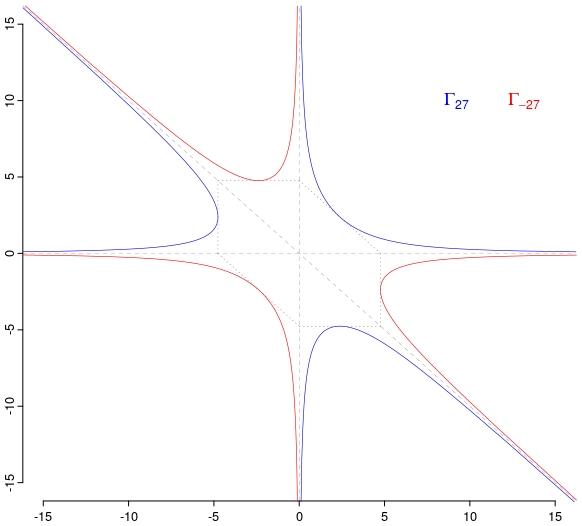
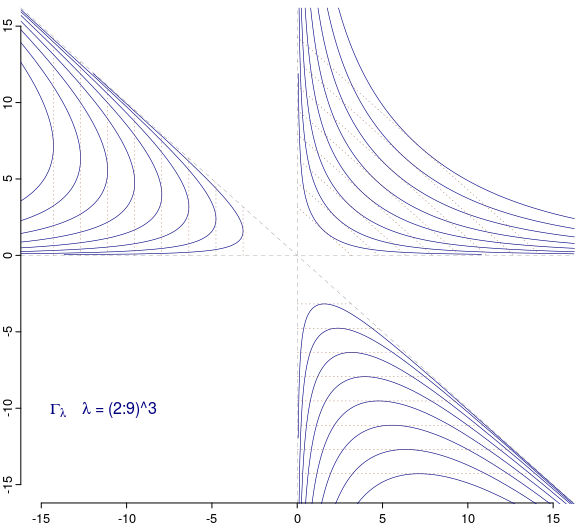
# funcţia care trasează Γλ (în forma polară) şi (ca segmente) liniile importante
plot_cubic <- function(L, col="blue") {
  t <- seq(0, 2*pi, len=1000)
  r <- sqrt3(L*sqrt(2)) / (sin(2*t)*sin(t + pi/4)) ^ (1/3)
  lines(r*cos(t), r*sin(t), lwd=0.6, col=col)
  v1 <- sqrt3(4*L); v2 <- 2*sqrt3(L/2)
  segments(c(-v1, 0, 0), c(0, -v1, v2), c(-v1, v1, v2), c(v1, -v1, 0), 
           lwd=0.4, lty="dotted", col="sienna4")
}

# Γ27 şi Γ-27
plot_cubic(27); plot_cubic(-27, col="red")
legend("topright", legend=c(expression(Gamma[27]), expression(Gamma[-27])), 
       text.col=c("blue", "red"), cex=1.1, horiz=TRUE, inset=c(0.05, 0.15), bty="n")

# Γλ, λ = 23, 33, ..., 93 (a doua imagine)
for(L in (2:9)^3)
  plot_cubic(L, col="navy")

Rădăcina cubică - de care am avut nevoie în câteva rânduri în funcţia plot_cubic() - se modelează de obicei prin "^(1/3)"; dar pentru numere negative, acest operator dă rezultate ca 'NaN' ("Not a Number") - iar în R aceasta nu stopează execuţia (cu vreun mesaj de eroare): funcţiile de plotare (ca lines() şi segments(), folosite mai sus) ignoră valorile 'NaN' (şi 'NA'). Tocmai de aceea, am introdus mai sus funcţia sqrt3() - dar am folosit-o numai pentru valori individuale, nu şi pentru calculul vectorului care apare ca "deîmpărţit" în expresia de calcul a razei polare 'r' (v. a doua linie din corpul funcţiei plot_cubic()); nu înţeleg exact de ce, dar am constatat că folosind sqrt3() (în loc de "^(1/3)") şi pentru acest "deîmpărţit", lines() interpretează cumva rezultatul respectiv şi plotează (pe lângă graficul funcţiei) şi liniile axelor şi celei de-a doua diagonele.

Pe graficele obţinute, constatăm (fără calculul cuvenit) că Γ_λ are trei asimptote concurente: axele de coordonate şi a doua bisectoare; un calcul direct (pe baza coordonatelor specificate mai sus în apelul segments()) confirmă intuiţia faptului că originea (punctul comun al asimptotelor) este chiar centrul de greutate al triunghiului format de "vârfurile" celor trei ramuri (punctele acestora care sunt cel mai apropiate de origine, în care sunt tangente segmentele punctate din figura de mai sus); a vedea eventual, cubica lui Tucker.