Daţi-mi un exemplu...
Dacă tot facem Excel pe la clasa a X-a şi algebră liniară pe la clasa a XI-a - hai să dăm un exemplu de sistem de ecuaţii liniare. Bineînţeles că sunt păţit: cerând elevilor de-a IX-a să-ţi zică despre mulţimea zilelor săptămânii, obţii mereu "luni, marţi, ..."; extrem de rar, dacă tot ceri răspunsuri - vei obţine poate "joi, luni, duminică, ..." sau poate "lundi, mardi, jeudi, ...". Cineva mi-a dat "exemplu" de sistem de ecuaţii "2x = 4, 2y = 4" şi a rămas foarte nedumerit: este un exemplu ingenios, putem adăuga la nesfârşit ecuaţii "2z = 4, 2t = 4, etc." - dar… nu prezintă interes; culmea este că i-am cerut să încerce un alt exemplu şi ingenios cum este, mi-a dat "3x=6, 3y=6, 3z=6"…
Poate că înţelegerea lucrurilor ar necesita un mic act de judecată. Cum adică "să dăm un exemplu…"? Ce "să dăm"? Ce este de dat într-o ecuaţie a sistemului: nişte coeficienţi - care pot fi aleşi oricum - şi un termen liber, care poate fi eventual dedus având dată o soluţie. Desigur (mai ales că am amintit de Excel, în cerinţa noastră), ar fi de bun simţ să evităm alegerile banale - recunoscând totuşi că putem reduce orice sistem liniar la o formă "banală", precum "2x=4, 2y=5, 2z=6".
Imaginea de mai jos redă o alegere pentru coeficienţii a trei ecuaţii cu câte trei necunoscute: celulele A1, B1 şi C1 conţin coeficienţii din prima ecuaţie, celulele A2, B2 şi C2 conţin coeficienţii din a doua ecuaţie, ş.a.m.d.; celulele din coloana A conţin coeficienţii primei necunoscute, celulele din coloana B conţin coeficienţii celei de-a doua necunoscute, ş.a.m.d.
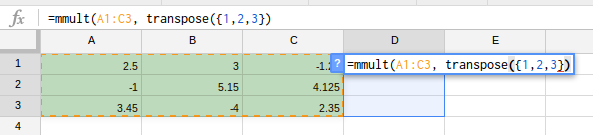
Să zicem că am vrea (1, 2, 3) drept soluţie a sistemului; termenii liberi necesari pot fi găsiţi înmulţind matricea A1:C3 cu vectorul-coloană al soluţiei (transpusul vectorului (1, 2, 3)). Am selectat celulele D1:D3 şi am tastat formula care se vede pe imagine, angajând funcţiile MMULT() care produce rezultatul înmulţirii a două matrice şi TRANSPOSE(), care furnizează transpusa unei matrice; în final tastăm combinaţia de două taste CTRL + ENTER (nu simplu ENTER, fiindcă rezultatul are de ocupat celulele grupate anterior D1:D3). Cu notaţia uzuală, sistemul rezultat este:
Cum am (re)găsi acum, soluţia acestui sistem? Selectăm de exemplu celulele A6:A8 şi tastăm =Mmult(Minverse(A1:C3), D1:D3), iar apoi CTRL + ENTER:
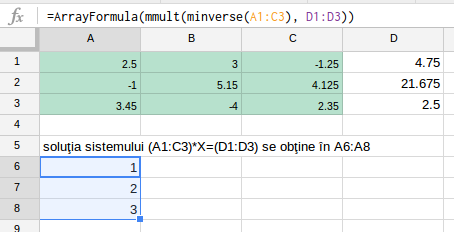
Putem avea diverse alte ilustrări ale faptului că am putea folosi Excel (sau Google Sheets de pe care am luat imaginile de mai sus, sau altă aplicaţie de calcul tabelar) drept suport pentru abordarea unor teme şi subiecte de matematică; dar este îndoielnic dacă este şi potrivit să procedăm astfel, de vreme ce dispunem de variante mai fireşti. De exemplu, putem folosi Octave:
octave:1> A = [2.5, 3, -1.25; -1, 5.15, 4.125; 3.45, -4, 2.35] A = 2.5000 3.0000 -1.2500 -1.0000 5.1500 4.1250 3.4500 -4.0000 2.3500 octave:2> B = A*[1; 2; 3] B = 4.7500 21.6750 2.5000 octave:3> X = linsolve(A, B) X = 1.00000 2.00000 3.00000
Am introdus matricea A (pe care o reprezentam în Excel prin celulele A1:C3), folosind ',' pentru a separa elementele unei linii şi ';' pentru separarea liniilor; apoi am calculat un vector coloană B şi am rezolvat ecuaţia A*X=B, invocând funcţia linsolve().
Putem imagina uşor (cu Octave, nu cu Excel) şi un exemplu ceva mai sofisticat:
octave:1> A = 100*(rand(4, 4) + i*rand(4, 4)) A = 47.2028 + 69.6538i 92.5993 + 81.6753i 68.6215 + 80.8788i 69.6419 + 20.6108i 66.6598 + 48.7040i 49.1259 + 31.5402i 4.6764 + 48.9171i 69.0974 + 42.1461i 10.8707 + 1.0906i 56.9541 + 49.2274i 93.7018 + 17.4943i 58.3932 + 38.2811i 21.9795 + 20.3255i 76.9878 + 22.1635i 45.9363 + 50.2709i 11.9255 + 10.3146i octave:2> B = 1000*(rand(4, 1) + i*rand(4, 1)) B = 511.635 + 442.013i 69.472 + 333.953i 586.874 + 48.402i 820.507 + 940.027i octave:3> X = A \ B X = -14.1068 - 3.7809i 4.4817 + 18.6102i 7.7250 - 13.2349i 4.7343 - 4.3140i
Am generat aleatoriu matricea complexă A (cu numere complexe ca elemente) şi un vector complex B; apoi am obţinut soluţia ecuaţiei matriceale AX=B (pe care o şi putem verifica: rezultatul A*X trebuie să coincidă cu vectorul B).
vezi Cărţile mele (de programare)