Faţă de [1], ne-a rămas încercarea (cam tulbure) de a investiga legăturile dintre orientarea iniţială a listei profesorilor, ordinea în care sunt abordate pe rând clasele şi numărul de ferestre de pe orarul obţinut; dacă am găsi ceva relevant, atunci vom putea şi să îmbunătăţim funcţia mountHtoDay() (prin care generăm orarele) sau măcar, ne vom da seama cum să o exploatăm cât mai bine, în situaţii concrete.

1. Cui putem impune, o anumită ordine?

În [1], generarea de orare pentru lecţiile <prof>|<cls> ale unei zile se petrece după următorul scenariu:

1. ordonăm, într-un fel sau altul, lista profesorilor (în setul lecţiilor zilei, <prof> este transformat în factor ordonat);
2. splităm setul tuturor lecţiilor zilei, pe clase (pentru fiecare clasă, lecţiile acesteia păstrează ordinea dictată de factorul comun <prof>);
3. pentru fiecare clasă, una după alta, încercăm să alocăm lecţiile acesteia pe orele 1..7 ale zilei; alocarea poate să eşueze, dacă intră în conflict cu alocarea pe ore făcută anterior unei alte clase (un profesor intră într-o aceeaşi oră la ambele clase);
4. dacă la un anumit moment, (III) eşuează pentru clasa curentă – atunci stopăm (III), schimbăm ordinea claselor şi reluăm (III) pentru noua ordine de clase.

Aplicând (III)+(IV) de un număr suficient de mare de ori (de ordinul zecilor, dar poate ajunge şi la ordinul miilor sau zecilor de mii), vom reuşi să alocăm toate lecţiile pe orele 1..7 ale zilei; dacă numărul de ferestre din orarul rezultat este prea mare, putem repeta (I)..(IV), obţinând un alt orar, poate cu mai puţine ferestre (amintim din [1], că pe orarele rezultate prin mountHtoDay(), profesorii au fie zero ferestre, fie una singură, fie două ferestre consecutive).

Să observăm că putem schimba cum dorim, ordinea profesorilor (la pasul (I)); dar ordinea claselor (la pasul (IV)) trebuie lăsată la voia întâmplării (angajând sample()) – altfel nu se poate garanta că repetând (III)+(IV), ajungem la un orar.
Desigur, dacă prin (I)..(IV) obţinem (în 10-20 minute) un orar cu „puţine” ferestre, atunci putem relansa programul indicând din start nu numai ordinea profesorilor, dar şi ordinea claselor (reconstituită din orarul rezultat iniţial) – reobţinând orarul respectiv, de data aceasta direct (fără (IV)), în doar o fracţiune de secundă (aşa am ajuns la exemplul cu 25 de ferestre (pentru 241 de lecţii) din [1]).

2. Ce rezultă, în cazul unei ordini arbitrare a profesorilor?

Prima investigaţie (v. şi programul "cedulas.R" din [1]) asupra orarelor care se pot obţine prin mountHtoDay() decurge cam aşa: repetăm (I)..(IV) de un anumit număr de ori (pe cât se poate, de mare) – fixând de fiecare dată, la pasul (I), o ordine arbitrară a profesorilor (prin sample()) şi apoi, repetând (II)..(IV) de un anumit număr de ori:

source("schedulesDay.R")
tbPC <- csv2tidy(3)  # lecţiile repartizate în ziua a 3-a
task <- setProfBits(tbPC)  # pasul (I) (cu ordine aleatorie a profesorilor)
trM <- map_df(1:100, function(i) {   cat(i, " ");
    TB <- task[[1]] %>% split(.$cls)  # pasul (II)
    Bits <<- task[[2]]
    NTRY <<- 0  # reiniţializează contorizarea încercărilor
    orZ <- mountHtoDay(TB)  # paşii (III)+(IV)
    ngaps <- sum(unlist(lapply(orZ[[2]], holes)))  # numărul total de ferestre
    data.frame(gaps = ngaps, ntry = NTRY)
})

Obs. De regulă, funcţiile map_() nu trebuie să producă „efecte laterale”; am folosit totuşi operatorul de atribuire globală, '<<-', fiind necesar aici să resetăm vectorul Bits al octeţilor de alocare (pe orele zilei) ai profesorilor (v. [1]).

Am rulat acest program de mai multe ori, obţinând (într-un timp care variază de la vreo 10-15 minute, până la una-două ore) 12 fişiere "trM{1-12}.RDS" cu câte 100, 200, 300 sau 400 de linii (sau „observaţii”) – fiecare consemnând numărul de ferestre $gaps şi numărul de încercări $ntry (v. (IV)) prin care s-a ajuns la orarul respectiv:

> trm <- readRDS("trM12.RDS")
> str(trm)
'data.frame':	400 obs. of  2 variables:
 $ gaps: num  51 53 46 50 47 51 39 49 53 53 ...
 $ ntry: num  51 32 313 32 10 33 57 40 133 49 ...

Reunim fişierele obţinute şi producem o histogramă a numărului de ferestre:

trm <- map_df(1:12, function(i) readRDS(paste0("trM", i, ".RDS")))
hist(trm$gaps)  # în total, avem 2700 orare

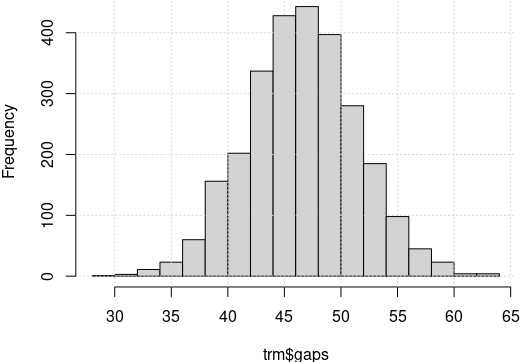
Putem concluziona astfel: dacă lăsăm la voia întâmplării ordinea profesorilor, orarele obţinute prin mountHtoDay() au cel mai adesea, un număr de 45-50 de ferestre (şi foarte rar, sub 35 sau peste 57 de ferestre); iar summary(trm$ntry) ne arată că numărul de încercări (IV) este cel mai adesea sub 300 (în 75% din cazuri).

3. Cazurile în care profesorii sunt ordonaţi după numărul de ore

Rescriem programul de mai sus, prevăzând în argumentul FUN din setProfBits() o funcţie care ordonează profesorii – crescător într-un caz, descrescător în celălalt – după numărul de ore pe care le au în ziua respectivă:

# traceMount3
source("schedulesDay.R")
tbPC <- csv2tidy(3)  # lecţiile repartizate în ziua a 3-a
prfOrd <- function(vp)  {  # ordonează profesorii după numărul de ore
    names(sort(table(tbPC$prof)))  # crescător
#   names(sort(table(tbPC$prof), decreasing=TRUE))  ## descrescător
}
task <- setProfBits(tbPC, FUN = prfOrd)  # pasul (I)
print(strftime(Sys.time(), format="%H:%M:%S"), quote=FALSE)
trM <- map_dbl(1:100, function(i) {     cat(i, "-", NTRY, " ", sep="");
    TB <- task[[1]] %>% split(.$cls)  # pasul (II)
    Bits <<- task[[2]]
    orZ <- mountHtoDay(TB)  # paşii (III)+(IV)
    sum(unlist(lapply(orZ[[2]], holes)))  # numărul total de ferestre
})
print(strftime(Sys.time(), format="%H:%M:%S"), quote=FALSE)
save(trM, NTRY, file="trM20.Rdata")

Obs. De data aceasta (cu map_dbl()), obţinem într-un vector, numărul de ferestre din orarele generate – mai simplu, decât să constituim cu valorile respective un obiect data.frame, cum făceam în programul din §2.

Iată cam ce obţinem în cazul când lecţiile fiecărei clase sunt aranjate conform ordinii crescătoare a numărului de ore pe zi ale profesorilor respectivi:

> source("traceMount3.R")  # ordonând profesorii crescător după numărul de ore
[1] 15:04:30
1-0  2-4  3-135  4-193  5-208  6-291  7-347  8-429  9-472  10-540  11-616  12-631
13-791  14-810  15-940  16-983  17-986  18-1006  19-1023  20-1026  21-1130  22-1204
## ... ##
86-5978  87-6009  88-6011  89-6043  90-6060  91-6093  92-6122  93-6228  94-6300 
95-6369  96-6432  97-6501  98-6510  99-6711  100-6904  
[1] 15:20:48  # durata execuţiei: 16 minute
> table(trM)
trM  # frecvenţa orarelor obţinute, după numărul de ferestre
37 38 40 41 42 43 44 45 46 47 48 49 50 51 52 53 
 3  1  4  8  1  9 11 10 13  6 12  5  6  5  3  3 
> NTRY
[1] 6925  # numărul total de încercări (IV)

S-a ajuns la primul orar după numai 4 încercări; la al doilea, după 135-4=131 de încercări; la al treilea, după 193-135=58 de încercări, etc. Pentru cele 100 de orare (obţinute în 16 minute) s-au făcut în total, 6925 de încercări (III)+(IV). 25% dintre orare (dar deocamdată, nu avem decât 100) au între 37 şi 43 de ferestre.

Bineînţeles că dacă repetăm execuţia programului vom obţine alte 100 de valori (se păstrează (I), dar ordinea claselor în (III) este mereu alta) – dar tot în vreo 15 minute şi cam cu aceeaşi distribuţie după numărul ferestrelor ca în cazul redat mai sus (vom vizualiza ceva mai jos această distribuţie, pentru 500 de orare).

Cazul în care lista profesorilor din (I) este orientată descrescător după numărul de ore ale acestora, se dovedeşte a fi cazul „cel mai rău”:

> source("traceMount3.R")  # ordonând profesorii descrescător după numărul de ore
[1] 22:56:51
1-0 2-7985 3-8284 4-8509 5-13060 6-13693 7-19735 8-21130 9-22281 10-23390 11-26196
12-44719 13-45511 14-48265 15-56825 16-62860 17-67802 18-70424 19-71704 20-75288
## ... ##
86-252357 87-258031 88-260499 89-262619 90-266666 91-272296 92-273549 93-275374
94-278254 95-278419 96-282561 97-282796 98-287047 99-293425 100-296825 
[1] 10:20:17  # durata execuţiei: peste 11 ore!
> table(trM)
trM  # frecvenţa orarelor obţinute, după numărul de ferestre
39 41 42 43 44 46 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 64 67 
 1  1  2  1  1  5  5  1  9 11 11 10  7  8  6  5  7  3  1  1  2  1  1 
> NTRY
[1] 297774  # numărul total de încercări (IV)

În acest caz, numărul de încercări (III)+(IV) prealabile constituirii unui orar este de ordinul miilor şi zecilor de mii, cu o durată medie de 6-7 minute pentru fiecare orar, iar numărul de ferestre este în foarte puţine dintre orarele obţinute, mai mic de 46.

Ne explicăm cât de cât această situaţie, astfel: dacă orele 1..7 sunt montate fiecărei clase începând cu profesorii care au cel mai multe ore în ziua respectivă, atunci vor rămâne din ce în ce mai puţine „portiţe” pentru lecţiile profesorilor de la sfârşit (care, având puţine ore în acea zi, apar la cel mult trei clase) – încât vor fi necesare foarte multe reveniri la pasul (III), până ce se va nimeri o ordine a claselor în care să nu mai apară conflicte între alocările succesive ale lecţiilor claselor, pe orele zilei.

Prin urmare, dintre cele două posibilităţi de ordonare explicită a listei profesorilor vizate mai sus, preferabilă este (fără nicio îndoială) prima – ordinea crescătoare a numărului de ore. Executând pentru cazul „crescător” "traceMount3.R", acum cu 1:500 în map_dbl(), rezultă (cam într-o oră şi ceva) această histogramă – reprezentativă pentru numărul de ferestre din orarele obţinute în cazul când profesorii sunt în ordinea crescătoare a numărului lor de ore:

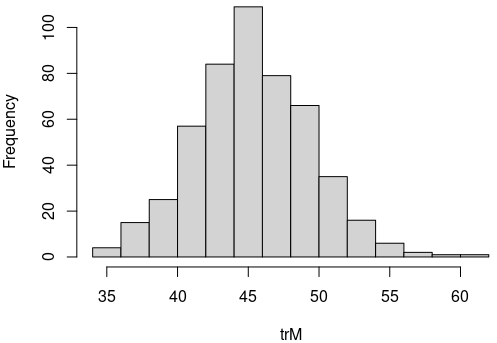
Putem confrunta cu §2 (unde ordinea profesorilor era una arbitrară), ţinând seama însă de faptul că în §2 aveam 2700 de orare, iar acum avem numai 500; pare clar că impunând în (I) ordinea crescătoare a numărului de ore, în loc de una aleatorie – avem mai mari şanse să obţinem orare cu mai puţin de 40 de ferestre (dar cel mai adesea, vom obţine orare care au în jur de 45 de ferestre).

4. Spre o „cea mai bună” ordine a profesorilor

În [1], listând orarul cu 25 de ferestre pe care-l obţinusem, exprimam bănuiala că pentru o obţine prin mountHtoDay() orare cu „puţine” ferestre, ordinea profesorilor trebuie să corespundă (în general) „cu aceea în care fiecare să aibă cât mai puţine clase în comun, cu cei care îl preced”; faptul evidenţiat la §3, că este de preferat ordinea crescătoare după numărul de ore – sprijină cumva această bănuială.

Dar în loc să investigăm cum sugeram în programul "cedulas.R" din [1] – generăm un număr suficient de mare de orare (folosind în (I) câte o ordine aleatorie a profesorilor) şi apoi, verificăm în ce măsură orarele cu „puţine” ferestre, dintre cele rezultate, satisfac bănuiala noastră – este preferabil să procedăm „pe dos”, astfel: la (I) ordonăm profesorii după un principiu precum cel exprimat în bănuiala menţionată şi apoi generăm prin (II)..(IV) un anumit număr de orare – rămânând să constatăm dacă orarele obţinute tind să aibă „puţine” ferestre.

Dar care „principii” de ordonare a listei profesorilor ar fi de testat, urmărind să obţinem orare „mai bune” decât cele din §3 (unde am avut în vedere ordonarea crescătoare după numărul de ore ale profesorilor)?
Ne-am putem inspira desigur, din teoria grafurilor…

Putem asocia setului iniţial de lecţii <prof>|<cls>, un graf în care vârfurile corespund lecţiilor respective şi muchiile unesc vârfuri care corespund unui aceluiaşi profesor sau unei aceleiaşi clase (deci unesc lecţii care nu se pot desfăşura simultan); orice colorare cu 1..7 a vârfurilor acestui graf (încât vârfurile adiacente să aibă culori diferite) reprezintă un orar al lecţiilor respective (şi invers).

În algoritmii secvenţiali de colorare a unui graf, ordinea stabilită iniţial pentru vârfuri depinde, într-un fel sau altul, de gradele vârfurilor (gradul fiind dat de numărul de adiacenţi ai vârfului respectiv); să observăm că în §3 nu am avut în vedere „gradul”, fiindcă prin „numărul de ore ale profesorului” am vizat numai partea <prof> a fiecărei lecţii – prin urmare, ar fi de văzut dacă luând în seamă acum („într-un fel sau altul”) şi partea <cls>, vom obţine orare „mai bune” decât cele din §3.