Cel mai mare divizor comun

În Excel şi în alte aplicaţii de tip Spreadsheet, avem funcţia GCD; introducând în celula B1 formula =gcd(A:A) obţinem cel mai mare divizor comun al numerelor înregistrate în coloana A:

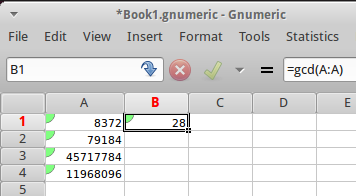
Întâlnim şi în alte locuri câte o funcţie "GCD" - dar desigur, doar pentru două numere (nu pentru o coloană de "oricâte" numere, cum pare firesc să avem într-o foaie de calcul tabelar); de exemplu, în Python avem funcţia fractions.gcd(a, b), iar în C++11 (în stl_algo.h) avem __gcd(__m, __n).

Pentru a obţine apoi GCD pentru o listă de oricâte numere, putem aplica reţeta clasică "divide et impera" (a vedea de exemplu get_cmmdc(T)), sau putem împrumuta schema funcţională fold:

foldl (#) e [x1, x2, ..., xn] = (...((e # x1) # x2) # ...) # xn

unde # reprezintă o operaţie binară asociativă (la stânga), iar e este o valoare iniţială sau eventual, elementul neutru al operaţiei; în Python "fold" apare ca reduce(function, sequence[, initial]) -> value (colapsare la o singură valoare finală, prin aplicarea succesivă a funcţiei binare indicate):

vb@Home:~$ python
>>> from functools import reduce
>>> from fractions import gcd
>>> reduce(gcd, [30, 12, 18, 24, 60])
6
>>> 

În C++ numele adoptat pentru "foldl" (în biblioteca numeric) este accumulate:

#include <iostream>
#include <numeric>
#include <algorithm>
using namespace std;
int main () {
    auto lst = vector<int>{30, 12, 18, 24, 60};
    cout << accumulate(begin(lst), end(lst), 0, __gcd<int>);
}

Funcţiile din libstdc++ (C++ Standard Library) sunt "parametrizate", iar std::__gcd() nu face excepţie, fiind definită pentru un tip de date - denumit _EuclidianRingElement - care permite "împărţirea cu rest" şi binecunoscutul algoritm al lui Euclid; în exemplul de program de mai sus am angajat un vector de numere întregi obişnuite, încât am "specializat" __gcd<int>.

În JavaScript reduce este o metodă proprie obiectului Array():

function gcd(a, b) { // cel mai mare divizor comun a două numere
    while(b) { 
        var t = b; 
        b = a % b; 
        a = t; 
    }
    return a;
};
console.log(
    [30, 12, 18, 24, 60].reduce(gcd)
);

Valoarea polinomului

Schema lui Horner evaluează un polinom (de o singură variabilă) folosind numărul minim posibil de operaţii: anxn + an-1xn-1 + ... + a1x + a0 = (...(anx + an-1)x + ... + a1)x + a0; cu alte cuvinte, asupra listei coeficienţilor - ordonată descrescător după grad - se aplică următoarea operaţie de reducere succesivă, luând rezultat = 0 ca valoare iniţială: rezultat *= x + coeficient_curent.

"Cel mai mare divizor comun" chiar merita scrierea unei funcţii separate gcd(a, b), indicată apoi ca parametru al reducerii; dar acum, operaţia care trebuie implicată în reducerea listei coeficienţilor până la valoarea finală este una extrem de banală - încât o vom modela direct în lista parametrilor reducerii, ca funcţie "anonimă" (sau, "expresie lambda").

În Python am avea următoarea formulare:

from functools import reduce  # Python3 a mutat reduce() în functools

def polinom(coef, x):
    return reduce(lambda a, b: a*x + b, coef)

print(polinom([1,1,1,1,1,1,1,1,1,1], 2)) # x^9 + x^8 + ... + x + 1 pentru x=2 

Deasemenea, putem formula mai interesant astfel:

def polinom1(coef):
    return lambda x: reduce(lambda a, b: a * x + b, coef)

Funcţia polinom1() returnează o funcţie:

pol = polinom1([1,1,1,1,1,1,1,1,1,1])
print( pol )
<function <lambda> at 0x7f93f0938668>

care poate fi invocată apoi pentru valoarea x dorită:

for x in range(3):
    print( pol(x) )
1
10
1023

În C++11 putem exprima astfel:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

#include <iostream>
#include <numeric>
#include <algorithm>
#include <complex>
using namespace std;

template<typename T> T polinom(vector<T> coef, T x) {
    return accumulate(begin(coef), end(coef), 
                      static_cast<T>(0), 
                      [x](T a, T b) { return a*x + b; }
    );
}

int main () {
    auto coef = vector<int>(10, 1); 
    cout << polinom(coef, 2) << endl;  // 1023
    auto ccoef = vector<complex<int>>{{1, 1}, {2, 3}, {3, -3}, {4, 5}};    
    cout << polinom(ccoef, {0, 1}) << endl;  // (6,4) adică 6 + 4i
}

Coeficienţii polinomului şi punctul în care trebuie evaluat acesta sunt de un acelaşi tip T, iar funcţia din liniile 7-12 obţine valoarea polinomului invocând algoritmul accumulate cu funcţia lambda redată în linia 10. În liniile 15-16 exemplificăm pe un polinom cu coeficienţi întregi (T = int), iar în liniile 17-18 am considerat un polinom cu coeficienţi complecşi întregi (T = complex<int>).

Construcţiile lambda din C++11 (dar nu şi cele din Python) pot să conţină diverse instrucţiuni (cu "efect lateral"); astfel, completând linia 10 cu cout << a << endl; (imediat înainte de return a*x+b;) putem trasa rezultatele intermediare - de exemplu, pentru cazul din liniile 17-18:

vb@Home:~$ g++ -std=gnu++11 -o pol polinom.cpp
vb@Home:~$ ./pol
(0,0)  // valoarea iniţială din linia 9, 0 + 0i
(1,1)  // (0,0)*(0,1) + (1,1) = (1,1) adică 1 + i
(1,4)  // (1,1)*(0,1) + (2,3) = (1 + i)*i + (2 + 3i) = (-1 + i) + (2 + 3i) = 1 + 4i
(-1,-2)  // (1,4)*(0,1) + (3,-3) = (1 + 4i)*i + (3 - 3i) = (-4 + i) + (3 - 3i) = -1 -2i
(6,4)  // (-1,-2)*(0,1) + (4,5) = (-1 - 2i)*i + (4 + 5i) = (2 - i) + (4 + 5i) = 6 + 4i

Calculul de mână cu care am acompaniat rezultatele redate mai sus este desigur important: numai stăpânind calculul manual şi convenţiile specifice limbajului are sens să-ţi propui automatizarea lui.

Am putut lucra cu diverse tipuri de polinoame, în programul C++11 de mai sus; vedem astfel unele dintre avantajele conferite de conceptele de programare parametrizată specifice pentru C++11. Pe de altă parte însă, în Python calculul cu orice fel de numere (inclusiv cu numere complexe, sau cu întregi mari) este deja "nativ" - nu necesită neapărat demersuri explicite prealabile. Astfel, reluând funcţia polinom1() de mai sus - chiar şi direct, în modul de lucru interactiv, de la prompt-ul liniei de comandă - putem obţine imediat rezultatul calculului descris mai sus:

vb@Home:~$ python
Python 2.7.6 (default, Jun 22 2015, 17:58:13) 
[GCC 4.8.2] on linux2
>>> def polinom1(coef):
...     return lambda x: reduce(lambda a, b: a*x+b, coef)
... 
>>> polc = polinom1([1+1j, 2+3j, 3-3j, 4+5j])  # coeficienţii din linia 17
>>> print polc(1j)  # {0, 1} (din linia 9) = 0 + i = "1j" (în Python)
(6+4j)  # reprezentarea string Python a numărului complex 6+4i = (6,4)
>>> 

Mai sus am exemplificat cum se face de obicei, prin coeficienţi întregi mici; dar este foarte bine în general, dacă suntem pregătiţi să ne gândim şi la exemple nebanale de lucru. Pentru cazul de faţă, iată o propunere de aplicaţie nebanală (dar nu dificilă): verificaţi că media aritmetică a valorilor unui polinom cu coeficienţi complecşi în vârfurile unui poligon regulat (cu mai puţine laturi decât gradul polinomului) este egală cu valoarea polinomului în centrul poligonului.

Desigur, vom calcula valorile polinomului folosind de exemplu funcţia polinom1(); dar cuvântul-cheie în enunţul de mai sus pare a fi "verificaţi" (având o infinitate de polinoame şi de poligoane). Ne bazăm - de ce nu - pe bunul simţ: dacă vom putea constata valabilitatea proprietăţii respective într-un număr mare de cazuri generate aleatoriu, atunci este foarte plauzibil ca ea să fie valabilă totdeauna.

Am începe cu obţinerea vârfurilor unui poligon regulat, dat find centrul şi unul dintre vârfuri:

  # pol.py
from math import pi, sin, cos
def poligon(n, center, initial):
    return [center + initial*(cos(2*k*pi/n)+sin(2*k*pi/n)*1j) 
            for k in range(n)]

De exemplu, pentru triunghiul echilateral cu un vârf în punctul (1, 1):

>>> from pol import poligon
>>> poligon(3, 0, 1+1j)
[(1+1j), (-1.3660254037844384+0.36602540378443893j), 
         (0.36602540378443793-1.3660254037844388j)]

Apoi trebuie repetată să zicem de 10000 de ori, o procedură precum următoarea: se generează aleatoriu un întreg n (numărul de vârfuri) între 3 şi să zicem, 100; se generează aleatoriu un întreg k (gradul polinomului) cuprins între n şi să zicem, 100; se generează aleatoriu coeficienţii polinomului, ca numere complexe (de tip complex<double>, cum am formula în C++); apoi se calculează valorile polinomului pe vârfurile poligonului şi se compară media aritmetică a lor cu valoarea polinomului în centrul poligonului: dacă diferenţa nu este neglijabilă, atunci stopăm procesul (proprietatea supusă verificării este falsă) - altfel îl reluăm până epuizăm numărul de repetări convenit iniţial.