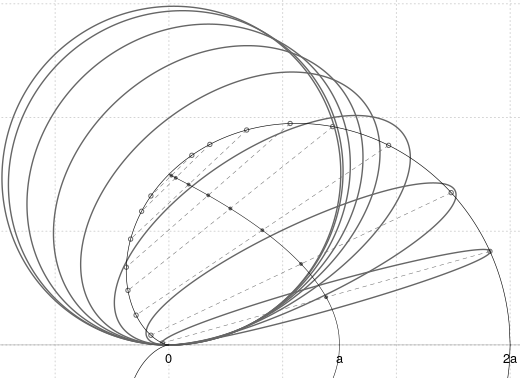
Pentru $a > 0$ şi $t\in(0,\frac{1}{2}]$, fie $b=4at(1-t)$. Având coeficienţii $$\begin{array}{@{}cll} A &=& ab \\ B &=& -2(a-b)\sqrt{ab} \\ C &=& a^2-ab+b^2 \\ E &=& -2ab\sqrt{ab} \\ \end{array}$$ ecuaţia $Ax^2+Bxy+Cy^2+Ey=0$ reprezintă o elipsă (de semiaxe $a$ şi $b$) tangentă în $\mathsf{O}$ axei $\mathsf{O}x$; când $t$ parcurge intervalul $[0,\frac{1}{2}]$, locul centrelor acestor elipse este un arc de parabolă (cu $\mathsf{O}x$ ca axă şi $(a,0)$ ca vârf) şi locul focarelor este o semi-cardioidă cu nodul în $\mathsf{O}$ şi cu $\mathsf{O}x$ ca bază.

Obs. Ecuaţia din enunţ reprezintă o elipsă tangentă în $\mathsf{O}$ axei $\mathsf{O}x$ oricare ar fi $a$ şi $b$ (cu $b\lt a$), fiindcă nu conţine $Dx$ şi termen liber (v. [3]); dar proprietăţile menţionate pentru centru şi focare au loc numai dacă $b=4at(1-t)$ pentru un $t\in[0,\frac{1}{2}]$.

Într-adevăr, în [2] am arătat că au loc proprietăţile menţionate pentru centrele şi focarele elipselor, în cazul când $A=4t(1-t)$, $B=-4(2t-1)^2\sqrt{t(1-t)}$, $C=16t^2(1-t)^2+(2t-1)^2$ şi $E=-16at(1-t)\sqrt{t(1-t)}$ (cu $t\in[0,\frac{1}{2}]$); înlocuind $t(1-t)$ cu $\frac{b}{4a}$ – plecând de la faptul arătat în [1] că pentru acest caz avem $b=4at(1-t)$ – se obţin uşor (dacă eliminăm în final, numitorul $a^2$) expresiile coeficienţilor din enunţul de mai sus (de exemplu, avem: $(2t-1)^2=4t(t-1)+1=1-\frac{b}{a}$).
Mai este de observat că $b=4at(1-t)$ asigură o corespondenţă biunivocă între $t\in[0,\frac{1}{2}]$ şi $b\in[0,a]$ (funcţia $t(1-t)$ fiind strict crescătoare pe intervalul $[0,\frac{1}{2}]$).

Bineînţeles că putem adapta programul din [2] (sau [3]), dar preferăm să scriem unul nou:

draw_ellipse_t <- function(a, t, ...) {
# a = semiaxa mare
# t = valoare între 0 şi 0.5 (determină unic semiaxa mică b, cu b < a)
# ... = parametri grafici de transmis funcţiilor de plotare
    b <- 4*a*t*(1-t)  # asociază biunivoc t din [0, 0.5] cu b din [0, a]
    A <- a*b; 
    C <- a^2 + b^2 - A
    xc <- a - b; yc <- sqrt(A)  # coordonatele centrului
    xlim <- c( -A/(sqrt(C)+xc) - 0.3, A/(sqrt(C)-xc) + 0.3 )
    ylim <- c( -0.3, 2*sqrt(A) + 0.3 )
    plot(0, type="n", asp=1, bty="n", xlab="", ylab="", xaxt="n", yaxt="n",
         xlim=xlim, ylim=ylim); grid()  # setează fereastra grafică
    B <- -2*xc*sqrt(A)
    E <- -2*A*sqrt(A)  #; print(c(A, B, C, E))
    x <- seq(xlim[1], xlim[2], by=0.01)
    y <- seq(ylim[1], ylim[2], by=0.01)
    z <- outer(x, y, function(x,y) A*x^2 + B*x*y + C*y^2 + E*y)
    contour(x, y, z, levels = c(0), drawlabels=FALSE, add=TRUE, ...)  # elipsa
    points(xc, yc, pch=19, cex=0.4, ...)  # centrul elipsei
    s <- sqrt(xc)
    F1 <- xc+s*sqrt(a) + 1i*(sqrt(A)+s*sqrt(b))
    F2 <- xc-s*sqrt(a) + 1i*(sqrt(A)-s*sqrt(b))
    points(c(F1, F2), cex=0.6, ...)  # focarele şi segmentul acestora
    segments(Re(F1), Im(F1), Re(F2), Im(F2), lwd=0.5, lty="dashed", ...)
    abline(h=0, lwd=0.2)  # tangenta în O(0,0)
    draw_pb_card(a)  # plotează arcul de parabolă şi cardioida
    text(1, -0.3, labels=paste("a =", a, "şi t =", t), cex=0.8, col="blue")
}

draw_pb_card <- function(a) {
    x <- seq(0, a, by=0.01)
    y <- sqrt(a*(a-x))
    points(x, y, type="l", lwd=0.6)  # arcul de parabolă (v. [1])
    points(x, -y, type="l", lwd=0.5)
    l <- seq(0, 1, by=0.001)
    x <- 2*a*l*(2*l-1)
    y <- 4*a*l*sqrt(l*(1-l))
    points(x, y, type="l", lwd=0.6, col="firebrick2")  # semi-cardioida (v. [1])
    points(x, -y, type="l", lwd=0.5, col="firebrick2")
}

draw_ellipse_t(a=4, t=0.25, col="blue")

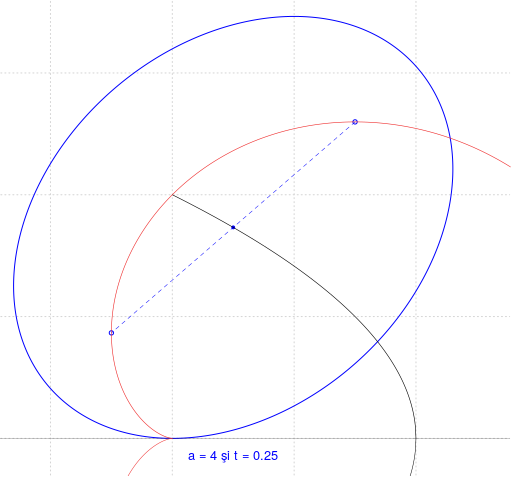
Mai precizăm (ceea ce este deja reflectat şi în programul redat) că centrele elipselor vizate în enunţ au coordonatele $x_c=a-b$ şi $y_c=\sqrt{ab}$, iar focarele au coordonatele $x_f=\pm \sqrt{a-b}\sqrt{a}+a-b$ şi $y_f=\pm\sqrt{a-b}\sqrt{b}+\sqrt{ab}$.

Este importantă pregătirea ferestrei grafice în care urmează să fie plotate punctele; în principal, aceasta înseamnă stabilirea în prealabil a limitelor de încadrare – în program, xlim şi ylim – a absciselor şi ordonatelor. Elipsa noastră este tangentă în $\mathsf{O}$ axei $\mathsf{O}x$ şi este situată deasupra acesteia, deci limita inferioară a ordonatelor punctelor elipsei este $0$; punctul "cel mai înalt" este simetricul lui $\mathsf{O}$ faţă de centrul elipsei (fiindcă în punctele simetrice faţă de centru, tangentele sunt paralele iar marginea de sus a boxei care conţine elipsa este paralelă cu $\mathsf{O}x$), deci limita superioară este $y_{\rm{max}}=2y_c=2\sqrt{ab}$.

Pentru xlim, avem de găsit abscisele punctelor în care elipsa are tangente verticale; aceste puncte sunt cele care anulează derivata în raport cu $y$, adică sunt acele puncte $(x,y)$ ale elipsei pentru care avem şi $Bx+2Cy+E=0$. Rezultă $Ax^2+y(Bx+Cy)+Ey=Ax^2+y(-Cy-E)+Ey=0$, de unde $Ax^2-Cy^2=0$, deci $y=\pm\sqrt{\frac{A}{C}}\,x\,$;   înlocuind în ecuaţia iniţială a elipsei, ajungem la $x=\pm\frac{E}{2\sqrt{AC}\,\mp\, B}$ - de unde rezultă valorile înscrise în program pentru xlim (în program am extins puţin limitele de încadrare - anume, cu $0.3$ - pentru a plota şi puncte suplimentare, ale cardioidei).

În [3] am stabilit "ecuaţia generală" a elipselor tangente în $\mathsf{O}$ axei $\mathsf{O}x$, în funcţia de semiaxele $a$, $b$ şi de unghiul polar $\theta$ al axei mari - găsind $B=-(a^2-b^2)\sin 2\theta$; egalând acum cu $B=-2(a-b)\sqrt{ab}$, obţinem $\sin 2\theta=\frac{2\sqrt{ab}}{a+b}$ şi rezultă că unghiul polar al axei mari este aici $\theta=\mathrm{arctg}\sqrt{\frac{b}{a}}$. Putem roti axa mare (încât unghiul polar al ei să difere de $\mathrm{arctg}\sqrt{\frac{b}{a}}$), păstrând semiaxele şi tangenţa în $\mathsf{O}$ la $\mathsf{O}x$ - dar elipsa obţinută astfel nu mai are proprietatea din enunţ a centrului şi focarelor.