De-a lungul parcursului şcolar de la noi, expresiile aritmetice sunt impuse în două etape mari; la clasele mici, adică vreme de vreo cinci ani (IV..VIII) - se poartă dulcegării de genul:

{ 12 + 3 x [ 20-2 x (7 - 10 : 5 ) ] +13 } x 10    

A vedea să zicem, "Azi, la matematica: Folosirea parantezelor in exercitii" şi probabil, diverse manuale şi culegeri de probleme pentru clasele IV-VIII.

Pe la clasa a IX-a încep corecturile şi standardizările:

(12 + 3(20 - 2)(7 - 10/5) + 13)×10 sau, mai bine (12 + 3*(20 - 2)*(7 - 10/5) + 13)*10

De fapt, corecturile necesare au putut fi intuite cu mult timp înainte, de oricare copil care va fi avut ideea (absolut firească) de a pasta într-o aplicaţie Calculator vreo expresie din manual - cu acolade şi cu paranteze pătrate, cu "x" în loc de caracterul uzual * (sau ×) şi cu ":" în loc de /.

Tot printr-a IX-a - ar putea începe reorientările şi reasimilările… De prin clasa a V-a, se tot deprind mecanisme de analiză sintactică şi morfologică a unui text (la "Limba română", dar şi la orele de "limbi străine"); iar aceste mecanisme servesc şi cazului mai simplu, al expresiilor algebrice (tot "texte", având asociate anumite "înţelesuri").

Propoziţiile corecte sunt constituite din anumite "părţi de vorbire", cu respectarea anumitor "reguli gramaticale" - a vedea programa şcolară pentru Limba şi literatura romănă, clasele V - VIII. Un limbaj oarecare presupune deasemenea, anumite "părţi de vorbire" specifice şi un set de "reguli gramaticale" pe baza căruia se pot produce "propoziţiile" (sau "programele") corecte.

Expresiile aritmetice angajează operatori şi operanzi; de exemplu, în expresia 52.25 + 37 avem operatorul binar "+" (desemnând operaţia de "adunare") şi operanzii numerici 52.25 şi 37. Aici vom considera numai operatori binari, iar drept "operanzi" primari - numai constante numerice.

Ceea ce ne interesează este valoarea expresiei. În limbajul natural, am putea exprima aceasta cam în trei moduri: fie mot à mot, prin Numărul 52.25 adunat cu numărul 37 ne dă … - fie prin Suma numerelor 52.25 şi 37 este … - fie prin Numerele 52.25 şi 37 au ca sumă ….

Prima dintre aceste trei exprimări "echivalente" este de-a dreptul oribilă, dar este practicată continuu la clasele mici…; a doua ar corespunde cel mai bine notaţiei prefixate a expresiei, + 52.25 37, sau chiar notaţiei "funcţionale" suma(52.25, 37); iar a treia reflectă notaţia postfixată 52.25 37 +.

Cele trei convenţii pentru determinarea operanzilor

Considerăm (deocamdată) numai expresii aritmetice în notaţia obişnuită - cea infixată: oricare operator este încadrat de către cei doi operanzi ai săi (vedem eventual mai târziu, că mecanismul de evaluare a expresiei se bazează totuşi pe forma postfixată, a acesteia). Această "încadrare" atrage însă nişte probleme, în cazul când expresia conţine mai mulţi operatori: care sunt operanzii care încadrează pe fiecare operator, în expresia 3+2*5? Operanzii lui + sunt 3 şi 2, sau sunt 3 şi (2*5)? Operanzii lui * sunt 2 şi 5, sau sunt (3+2) şi 5? Într-un caz valoarea expresiei ar fi 25, în celălalt valoarea ei ar fi 13 - ori fiecare expresie ar trebui să aibă o valoare unică.

O soluţionare posibilă constă în parantezarea fiecărei subexpresii (şi chiar, a fiecărui operand), astfel că fiecare operator este încadrat de două subexpresii parantezate a căror evaluare va furniza în mod unic, operanzii necesari; expresiile corecte ar arăta atunci cam urât: fie (3)+((2)*(5)) (cu valoarea 13), fie ((3)+(2))*(5) (cu valoarea 25).

Această supra-parantezare are (azi…) un aspect hilar: adăugăm paranteze (scăpând de dileme), dar trecând ulterior la forma postfixată (baza mecanismului tipic de evaluare) - eliminăm toate parantezele. Putem preciza că totuşi, aşa se proceda în prima versiune de FORTRAN (vezi mai jos).

Dar soluţia standard pentru evitarea echivocităţii se bazează pe câteva convenţii simple; mai întâi, una referitoare la ordinea operaţiilor: ridicarea la putere (pentru care vom folosi aici ^) "leagă" mai tare decât înmulţirea şi împărţirea, iar acestea leagă mai tare decât adunarea şi scăderea. Ţinând cont de această ordine, expresia 3+2*5 devine una "corectă" (având asociată o valoare unică, 13): fiindcă la dreapta operandului 2 figurează *, iar acesta este "mai tare" ca + - rezultă în mod implicit că operanzii lui + sunt 3 şi (2*5) (iar nu 3 şi 2).

Din acest mic exemplu de analiză vedem că nu ajunge să citim (de la stânga spre dreapta) primul operand, apoi operatorul şi apoi al doilea operand - va trebui scanat şi următorul caracter, iar aceasta va fi suficient pentru a decide cum se evaluează corect subexpresia respectivă.

O a doua convenţie amendează ordinea operaţiilor: folosim paranteze (rotunde) pentru a forţa o altă ordine de operare decât cea standard. Astfel, expresia (3+2)*5 are valoarea 25: * are prioritate faţă de +, dar subexpresia sumă 3+2 este parantezată - deci devine operand al înmulţirii cu 5.

Dacă parcurgând expresia, întâlnim "(" - atunci ştim că urmează o "subexpresie", a cărei valoare devine operand fie pentru operatorul care urmează acesteia, fie pentru cel care o precede.

O a treia (şi ultima) convenţie vizează evaluarea subexpresiilor fără paranteze care angajează repetat un acelaşi operator: operanzii se determină prin "grupare la stânga" în cazul operatorilor {+, -, *, /} şi respectiv, prin "grupare la dreapta" în cazul operatorului ^. Astfel, 9-4-3 echivalează cu (9-4)-3 (prin grupare la stânga) şi nu cu 9-(4-3); iar 2^3^2 echivalează cu 2^(3^2) (prin grupare la dreapta, având valoarea 512) şi nu cu (2^3)^2 (care are valoarea 16).

Cele trei convenţii amintite mai sus permit recunoaşterea drept "corectă" sau nu, a oricărei expresii aritmetice (cu format infixat). De exemplu, 5+3+2*3^ nu este corectă (nu i se poate asocia o valoare, fiindcă lipseşte al doilea operand pentru ^); 5+3+2*3^0.5 este corectă (având valoarea aproximativă 11.464101615 - determinată pastând fără nici o jenă, într-o aplicaţie Calculator), ca şi 5+3+(2*8)^0.5 (de valoare 12; de data aceasta, recunoscând că este vorba de radicalul lui 16 - n-a mai fost nevoie de Calculator); expresia ((3)+(2))*(5) deşi conţine paranteze inutile - este corectă, ca şi expresia (3)+((2)*(5)) (în care toate parantezele sunt inutile); expresii ca 3+2)*5, [3+2)*5, [(3+2)*5+10]/5 sunt evident incorecte (trebuie folosite numai paranteze rotunde, iar acestea trebuie să fie balansate).

Să observăm că particularităţile unora dintre operatori conduc totuşi, la o anumită dilemă: este sau nu este "corectă", o expresie ca 7/(3-3), sau ca ((-2)*8)^0.5? Ambele sunt corecte din punct de vedere sintactic, dar asocierea corespunzătoare a unei valori devine o chestiune "de gust"; eventual, putem folosi ∞ (simbolul "infinit") pentru rezultatul împărţirii la zero (trebuind definite şi celelalte operaţii, pentru cazul de operand "infinit") şi eventual, putem extinde domeniul numeric obişnuit la numerele complexe (a doua expresie de mai sus are valoarea 4i). Ar fi de ţinut seama de faptul că ambele "soluţii" fiinţează ca atare în diverse aplicaţii Calculator - încât am putea decide să acceptăm drept "corecte" şi asemenea expresii.

Originile automatizării interpretării expresiilor

Până prin 1950, calculatoarele erau programate folosind codul maşină (şi ceva limbaj de asamblare); realizarea astfel, a unor programe complexe era o sarcină dificilă şi foarte costisitoare. Furnizorul principal de calculatoare era IBM şi aici s-a lansat proiectul realizării unui limbaj de programare "de nivel înalt" - care să fie uşor de însuşit de către programatori, independent de maşină şi adecvat cât mai multor împrejurări de folosire a calculatorului; dar în primul rând, el trebuia să asigure tratarea expresiilor matematice complexe în manieră similară notaţiei algebrice obişnuite (calculatoarele fiind utilizate la acea vreme în special în mediile stiinţifice).

John Backus este cel care a creat primul limbaj de programare de nivel înalt (şi primul compilator) - denumit FORTRAN (IBM Mathematical FORmula TRANslation System). Formalizarea adoptată pentru expresiile algebrice se poate vedea pe acest extras de pe manualul FORTRAN din 1956:

Ansamblul acestor reguli de producere a expresiilor este forma incipientă a notaţiei BNF; aceasta serveşte pentru descrierea consistentă a structurii unui limbaj, într-o formă uşor de translatat în limbaje de programare - încât scrierea codului necesar pentru recunoaşterea şi pentru evaluarea expresiilor corecte devine o sarcină de rutină (automatizată chiar, prin instrumente ca Flex şi Bison; unele interpretoare sau compilatoare şi unele aplicaţii Calculator includ direct, analizorul obţinut în prealabil prin intermediul acestor instrumente generice).

În Prolog (apărut prin 1970) s-a conceput o formalizare analogă cumva notaţiei BNF - anume DCG: regulile gramaticale sunt exprimate printr-un set de axiome (date ca implicaţii logice, sau "clauze") şi a valida o expresie înseamnă a o deduce logic din axiomele respective; iar sistemele Prolog includ un handler DCG care - analog instrumentelor pentru BNF amintite mai sus - transformă direct o definiţie DCG dată, într-un program executabil intern care permite analiza şi eventual generarea expresiilor corecte, în limbajul definit de gramatica respectivă.

Categorii de operanzi, reguli de potrivire şi mecanisme de analiză

Aşadar, expresiile aritmetice sunt formate din operanzi şi operatori, folosind paranteze şi respectând cele trei convenţii amintite ceva mai sus. Dar "operanzii" nu sunt neapărat, constante numerice primare; la stânga sau la dreapta unui operator pot figura şi subexpresii (parantezate sau nu): în expresia 20 - 14 / 5 * 2 ^ 2 ^ 3, operanzii lui * nu sunt 5 şi 2, ci subexpresiile 14/5 (operatorii / şi * au aceeaşi prioritate, iar gruparea decurge de la stânga spre dreapta) şi respectiv 2^2^3.

Am putea deosebi următoarele categorii de operanzi posibili:

— Primar - fie o constantă numerică imediată, fie (Expresie)   (subexpresie parantezată)

— Factor - fie Primar, fie de forma Primar^Factor   ("Factor" fiind la dreapta operatorului ^)

— Termen - fie Factor, fie Termen*Factor, fie Termen/Factor   (termenii fiind grupaţi la stânga)

— Expresie - fie Termen, fie Expresie+Termen, fie Expresie-Termen.

Este de subliniat că această alegere de "părţi de vorbire" constitutive ale expresiilor algebrice are un caracter convenţional - spre deosebire de cazul limbajelor naturale (Limba română, de exemplu), unde părţile de vorbire (substantiv, verb, adjectiv, etc.) sunt concepte de sine stătătoare, studiate ca atare.

Pentru exemplu, să interpretăm cu aceste definiţii 20-(14/5*2)^3, citind de la stânga spre dreapta: 20 este în primul rând Primar; urmează "-", dar nu avem o potrivire cu "Primar-". Putem substitui Primar cu Factor, dar nici aşa nu reuşim o potrivire cu definiţiile de mai sus; la fel, dacă substituim acum Factor cu Termen. Dar putem substitui mai departe Termen cu Expresie - rezultând potrivirea cu regula "Expresie-Termen"; deci expresia iniţială este corectă dacă la dreapta caracterului curent "-", vom depista un Termen.

Urmează "(" şi conform primei definiţii trebuie să urmeze Expresie şi apoi neapărat, ")". Explorarea continuă în această manieră - substituind ierarhic o categorie cu alta pentru a ajunge la o potrivire cu regulile date; dacă reuşim să "consumăm" astfel toate caracterele din expresia iniţială (găsind câte o potrivire la fiecare pas), atunci expresia respectivă este corectă.

Într-o primă aproximare a lucrurilor, definiţiile de mai sus se pot translata imediat în următorul mecanism de funcţii mutual recursive (schiţând un "analizor" de expresii aritmetice):

Primar() {
    IF(nextChar() este '(') { 
        extractNextChar(); Expresie();
        IF(nextChar() este ')') extractNextChar();
        ELSE THROW error("Parantezele nu sunt balansate");
    }
    ELSE {
        IF(nextChar() este cifră) extractNumber();
        ELSE THROW error("Numeric invalid");
    }
}
Factor() {
    Primar();
    IF(nextChar() este '^') { extractNextChar(); Factor(); }
}
Termen() {
    Factor();
    IF(nextChar() este '*' sau '/') { extractNextChar(); Termen(); }
}
Expresie() { // startează validarea expresiei
    Termen();
    IF(nextChar() este '+' sau '-') { extractNextChar(); Expresie(); }
}

nextChar() furnizează caracterul următor celui curent (dar nu modifică starea de "caracter curent"); extractNextChar() extrage caracterul curent (îl "şterge", avansând poziţia caracterului curent); iar extractNumber() consumă cifrele consecutive şi produce valoarea numerică aferentă. Ca pentru o "primă aproximare" - am ignorat posibilitatea unor caractere "spaţiu" intermediare.

Presupunând dată o expresie (într-o "zonă globală"), dacă apelul Expresie() se încheie "normal" - atunci expresia respectivă este corectă; altfel, pentru cazul unei expresii incorecte - THROW va transfera execuţia către o subrutină care produce anumite mesaje de eroare.

Fiindcă validarea trebuie declanşată apelând Expresie() - simbolul Expresie devine primordial între cele patru categorii sintactice definite mai sus (este "simbolul de start" al gramaticii).

Evidenţierea structurii expresiilor, prin parametrizare

Pseudocodul constituit cam "în fugă" mai sus, vizează doar validarea expresiei (este sau nu este corectă, expresia dată). Se pun în mod firesc diverse alte probleme: determinarea efectivă a valorii expresiei, transformarea ei în diverse alte formate (inclusiv, implicând anumite "limbaje de marcare"), evidenţierea structurii expresiei (eventual, chiar şi în mod grafic); toate acestea pot fi atinse, dacă parametrizăm funcţiile de mai sus cu câte o referinţă la o anumită structură de date înlănţuite, convenabilă pentru înregistrarea operatorului curent şi a celor doi operanzi ai săi:

struct Node { // reprezintă o "subexpresie"
    char operator;
    struct Node* operand_1; // pointer la primul operand (tot o structură Node)
    struct Node* operand_2; // pointer la al doilea operand
};

De exemplu, expresia 2+3*4 s-ar reprezenta simplificat prin Node('+', 2, Node('*', 3, 4)) - simplificarea constând în faptul că valorile "primare" (constantele numerice) sunt reprezentate ca atare şi nu printr-o construcţie Node(). O exemplificare de construcţie a unei astfel de reprezentări prin arbori binari se poate vedea şi în [1].

Angajând o asemenea parametrizare, funcţiile de mai sus s-ar rescrie cam aşa:

Expresie(Node& tree) { // zonă în care se va construi arborele expresiei
    Node tmp; // pentru arborele unei subexpresii
    Termen(tree);
    IF(nextChar() este '+' sau '-') {
        char operator = getNextChar();
        Expresie(tmp); // construieşte subarborul
        buildNode(operator, tree, tmp); // arborele expresiei
    }    
}

Obţinând reprezentarea internă (în memorie) ca Node() - orice prelucrare a expresiei date iniţial revine la parcurgerea arborelui respectiv (în preordine, în postordine, etc.), prelucrând după caz nodul curent vizitat.

Date interne ('struct' în C) versus notaţie (termeni Prolog)

Ca notaţie, construcţia (de structură C++ internă) de mai sus " Node('+', 2, Node('*', 3, 4))" aminteşte de ceea ce se cheamă "termeni compuşi" în Prolog (vezi eventual [2]):

vb@vb:~/clasa11/TREES$ prolog  /* SWI-Prolog (http://www.swi-prolog.org) */
?- assert(node(Operator, Operand1, Operand2)).
true.    % s-a adăugat în baza de date Prolog, termenul "node"
?- listing(node).
node(_, _, _).    % predicat de 3 variabile (anonime), totdeauna "true"
true.
?- node('+', 2, node('*', 3, 4)).
true.    % cele 3 variabile sunt substituite cu +, cu 2 şi respectiv cu node('*', 3, 4)
?- Tree = node('+', 2, node('*', 3, 4)).
Tree = node(+, 2, node(*, 3, 4)).    % Arborele sintactic al expresiei 2+3*4

Dar în Prolog, "orice este un termen" - inclusiv, expresiile aritmetice (term este singurul tip de date, cu câteva subtipuri); iar un termen Prolog este deja o structură precum Node (şi nu mai trebuie să o "definim", cum am făcut mai sus pentru C++).

În limbajele "obişnuite", 3 * 4 este o expresie care are o valoare - dar în Prolog este pur şi simplu termenul *(3, 4), compus din "functorul" (un nume atomic) * şi două argumente numerice (pe rol de "subtermeni"); iar "=" are sensul de "potrivire" - A = B fiind de fapt termenul =(A, B):

?- X = 2 + 3 * 4, write_canonical(X), is(Y, X).
+(2,*(3,4))    % forma "canonică" a expresiei 2 + 3*4 (ca termen Prolog)
X = 2+3*4,    % "unifică" variabila X şi termenul din partea dreaptă
Y = 14.    % unifică variabila Y şi termenul reprezentat de valoarea expresiei
?- is(20, 2+3*4).    % sau infixat:  20 is 2+3*4
false.    % termenii numerici 20 şi 2+3*4 NU se potrivesc
?- is(14, 2+3*4).
true.    % termenii numerici 14 şi 2+3*4 se potrivesc (14 este valoarea expresiei)

Argumentele sunt ataşate operatorilor, în ordinea crescătoare (inversă faţă de limbajul C: ^, apoi * şi /, apoi + şi -) a priorităţilor acestora:

2 + 3 * 4    % expresia dată
2 + *(3, 4)    % ataşează * (prioritate 400)
+(2, *(3, 4))    % ataşează + (prioritate 500)

Predicatul predefinit write_canonical(Term) afişează în formă prefixată (ca functor(arg1, arg2,...,argn)) termenul furnizat ca argument; iar is(Val, Expr) - care se poate scrie şi infixat, Val is Expr - evaluează numeric termenul Expr şi testează "potrivirea" variabilei Val cu valoarea rezultată (în cazul în care Val a fost instanţiată anterior cu un anumit termen), sau asigură unificarea acestora.

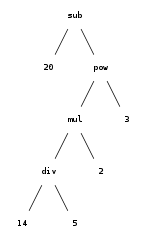
Pentru expresia 20-(14/5*2)^3 analizată parţial anterior, obţinem:

?- write_canonical(20-(14/5*2)^3).

-(20,^(*(/(14,5),2),3))  % arborele sintactic pentru 20-(14/5*2)^3
% sau cu alţi termeni:  sub(20, pow(mul(div(14, 5), 2), 3))

write_canonical/1 ne-a dat în fond, o exprimare textuală a arborelui de sintaxă al expresiei (anume, forma prefixată a expresiei); o redare grafică obişnuită pentru arborii de sintaxă, avem în imaginea alăturată (folosind termeni atomici standard sub, mul, etc. pentru operatori).

Studiul gramaticii expresiilor aritmetice, folosind Prolog

În exemplificările precedente ne-am ghidat după o regulă familiară: "se citeşte de sus în jos şi de la stânga spre dreapta" - intuind un mecanism de analiză LL(1), bazat pe aceste trei principii:

— parcurgem expresia dată de la stânga spre dreapta ("Left-to-right");
— căutăm să "potrivim" termenul curent din expresie cu una dintre definiţiile structurale prevăzute pentru "Expresie Aritmetică", începând cu cel mai din stânga ("Leftmost") element al definiţiei;
— în cazul în care nu putem decide în mod univoc, cărei definiţii se potriveşte termenul curent - ne uităm şi la caracterul următor acestuia în cadrul expresiei ("look ahead" = 1).

În general vorbind, o gramatică trebuie să specifice regulile după care trebuie grupate cuvintele, pentru constituirea propoziţiilor corecte în limbajul respectiv. Mai sus am imaginat o gramatică pentru expresii aritmetice, alegând ca neterminali {Primar, Factor, Termen, Expresie} şi precizând regulile după care poate fi expandat fiecare, astfel încât să obţinem sau să recunoaştem, o expresie formată numai din terminali (operanzi numerici, operatori şi eventual paranteze); am schiţat totodată, cum se pot implementa aceste reguli, într-un limbaj de programare sau altul.

Dar în Prolog nu avem nevoie să creem vreun program de implementare a regulilor gramaticale - Prolog a avut în vedere de la bun început procesări specifice limbajelor naturale, inclusiv regula "citeşte de sus în jos şi de la stânga spre dreapta" (mecanismul LL(1)). Proprietăţile unei gramatici sunt mult mai uşor de investigat folosind Prolog, decât dacă am folosi alte limbaje de programare.

O gramatică incipientă (descrierea sumelor de termeni identici)

Reluăm exact definiţia considerată anterior pentru Expresie, dar reducând-o la o singură operaţie:

% arith.pl
expr --> term | expr, [+], term.  % Expresie: fie Termen, fie Expresie+Termen
term --> [a].                     % Termen: un simbol final - fie a

Am formulat astfel o gramatică - în notaţie DCG ("Definite Clause Grammar") - cu doi neterminali (expr şi term), cu doi terminali ('a' şi '+') şi cu două reguli de expandare. Lansând interpretorul de Prolog, încărcând "arith.pl" şi folosind predicatul predefinit listing(expr) - constatăm că definiţia lui expr a fost transformată deja în următorul program Prolog:

expr(A, B) :-  % expr --> term | expr, [+], term
	(   term(A, B)    % prima alternativă de expandare: term
	;   expr(A, C),   % a doua alternativă: expr + term
	    C=[+|D],
	    term(D, B)
	).

Prolog (handler-ul de DCG existent) a adăugat câte două argumente A, B fiecărui neterminal DCG; aceste argumente sunt liste Prolog: C este unificat cu lista [+|D] (care începe cu '+' şi trebuie să continue cu o altă listă); pe de altă parte, devine obligatoriu ca terminalii să fie reprezentaţi în DCG prin liste (ca [a], [+] şi nu altfel). Prima dintre ele (variabila A, respectiv D) reprezintă secvenţa care trebuie analizată ("input"-ul), iar a doua (B) reprezintă secvenţa rămasă în final ("output"-ul), după încheierea etapei curente de analiză.

Dacă invocăm expr(Expr, []), indicând ca prim argument o variabilă Prolog (al doilea fiind lista vidă [], dat fiind că recunoaşterea unei expresii corecte trebuie să epuizeze toată lista de intrare) - aceasta va fi unificată pe rând cu fiecare expresie recunoscută de gramatica formulată mai sus:

?- expr(Expr, []).
Expr = [a] ;    % a (continuăm, tastând ;)
Expr = [a, +, a] ;    % a + a 
Expr = [a, +, a, +, a] .  %  a + a + a (stopăm aici, tastând .)

Este normal că acest proces continuă la nesfârşit, gramatica dată descriind într-adevăr toate sumele de termeni 'a'; dar iată (trasând execuţia, prin comanda ?- trace.) ce se petrece pentru cazul unei expresii care n-ar trebui să fie acceptate:

[trace]  ?- expr([b], []).    % expresia b ar trebui să fie respinsă (dar în timp finit!)
   Call: (6) expr([b], []) ? creep
   Call: (7) term([b], []) ? creep    % încearcă prima alternativă de expandare
   Fail: (7) term([b], []) ? creep    % b NU este un "term" 
   Redo: (6) expr([b], []) ? creep    % revine şi încearcă a doua alternativă
   Call: (7) expr([b], _G1105) ? creep    % "reapelează" expr() (la nesfârşit!)
   Call: (8) term([b], _G1105) ? creep
   Fail: (8) term([b], _G1105) ? creep

expr a fost expandat întâi prin term. Constatând că term([b], []) eşuează ("Fail": (7)) - s-a încercat a doua alternativă din definiţia pentru "expr"; dar aceasta înseamnă aici expandarea lui expr prin expr - astfel că se intră într-o buclă infinită expr -> term (Fail) -> expr -> term (Fail) -> expr ş.a.m.d., execuţia normală (nu sub "[trace]") încheindu-se cu ERROR: Out of local stack.

Eliminarea recursivităţii la stânga ("left-recursion")

Problema tocmai evidenţiată mai sus n-ar mai apărea, dacă am schimba ordinea neterminalilor din cadrul celei de-a doua alternative a clauzei expr:

% arith.pl
/*
expr --> term | expr, [+], term.  % left-recursion (inacceptabil pentru LL(k))
term --> [a].
*/
expr --> term | term, [+], expr.  % right-recursion (sau tail-recursion)
term --> [a].

În această nouă versiune, dacă term eşuează - atunci eşuează şi conjuncţia "term, [+], expr" (fără a se mai ajunge la momentul re-expandării lui "expr"); prin urmare eşuează ambele clauze din "expr", încât acum expr([b], []) se va încheia corect (cu "false"). Să observăm însă că term apare ca fiind "apelat" de câte două ori (ca prima alternativă şi respectiv la debutul celei de-a doua); metoda tipică pentru evitarea acestei redundanţe constă în înlocuirea alternanţei (marcate cu "|") prin conjuncţia (marcate cu ",") dintre termenul care s-a dovedit redundant şi o clauză suplimentară rest, aferentă părţii neredundante (posibil vidă) - conducând la această versiune "finală":

% arith.pl
/*
expr --> term | term, [+], expr.  % right/tail-recursion
term --> [a].
*/
expr --> term, rest.     % Expresie începe cu Termen, urmat de Rest-ul expresiei
rest --> [+], expr | []. % Rest-ul este +Expresie sau este vid
term --> [a].

Doar că schimbarea ordinii neterminalilor - făcând posibil mecanismul LL(1)) - va determina (cum am şi exemplificat mai la început) schimbarea arborelui sintactic: prima versiune (cu "left-recursion") va asocia termenii la stânga (ca (a+a)+a), în timp ce a doua versiune (cu "right-recursion") îi va asocia la dreapta (ca a+(a+a)); vom vedea acuşi că putem "forţa" totuşi lucrurile, parametrizând termenii.

Capturarea termenilor arbitrari (ideea parametrizării)

Cu o parametrizare foarte simplă, putem forţa gramatica de mai sus să recunoască orice sumă de termeni (nu numai de termeni 'a') - de exemplu a+b+c, sau xy+yz+zx:

% arith.pl
expr    --> term(_), rest.
rest    --> [+], expr | [].
term(X) --> [X].  % term(A, [A|B], B). (X "reţine" primul element din lista de intrare)

Modificarea constă în adăugarea unui parametru, neterminalului term; definiţia term(X) --> [X] spune că term(X) poate fi înlocuit cu lista [X], conţinând ca unic element termenul Prolog cu care este unificată curent variabila X. Prolog va transforma această definiţie în clauza term(A, [A|B], B) - adăugând (cum am precizat deja mai sus) două argumente: lista de intrare [A|B] conţine elementele care mai trebuie analizate la momentul respectiv; capul acestei liste este extras în A - urmând să fie unificat cu variabila anonimă din "apelul" term(_) - şi restul (elementele rămase de analizat) este furnizat în lista de ieşire B:

?- expr([3.14, +, x*y, +, f(x,y)], []).
true .  s-a recunoscut expresia-sumă (de termeni arbitrari): 3.14 + x*y + f(x,y)

?- listing(expr).
expr(A, C) :-  % A = [3.14, +, x*y, +, f(x,y)]
	term(_, A, B),  % unifică _ cu 3.14; rămâne de analizat B = [+, x*y, +, f(x,y)]
	rest(B, C).  % va analiza restul B

Completând comentariile de pe listingul tocmai redat - rest(B, C) va captura [+] din lista [+, x*y, +, f(x,y)] primită ca "input" şi va transmite restul acestei liste lui expr; reintrând acum în expr, term va captura termenul "x*y" şi va transmite lui rest lista rămasă [+, f(x, y)]; urmează extragerea lui [+] şi apoi reluând expr, se va captura şi "f(x,y)" - iar lista vidă rămasă va fi recunoscută de clauza a doua din definiţia lui rest (încât Prolog răspunde "true": expresia respectă gramatica indicată).

Explicitarea semnificaţiei unei expresii (ideea parametrizării)

Mai sus, când am invocat expr(Expr, []) am obţinut Expr = [a, +, a, +, a], trebuind să înţelegem că este vorba de "a + a + a" (sumă de trei termeni). Parametrizând corespunzător, putem să explicităm lucrurile - de exemplu sub forma add(a, add(b, c)), reprezentând chiar un arbore sintactic. Nu avem aici o "funcţie" (în sensul clasic), ci doar o notaţie sintetică - termenul add(T1, T2) desemnează un arbore având ca rădăcină "add" şi ca fii, cele două argumente:

% arith.pl
expr_test(add(T1, T2)) --> term(T1), term(T2).
term(A) --> [A].

?- expr_test(T, [a, b], []).
T = add(a, b).

?- expr_test(add(5.25, 3.14), X, []).
X = [5.25, 3.14].

Clauza DCG expr_test are ca parametru termenul compus add(T1, T2), convenind un anumit înţeles pentru listele formate din doi termeni, [T1, T2]; primul test redat obţine în variabila T semnificaţia atribuită listei de intrare [a, b], iar a doua invocare procedează invers - obţinând în X intrarea care (conform definiţiei DCG date) s-ar traduce prin add(5.25, 3.14).

Aplicând oarecum mecanic această schemă de parametrizare, putem reformula gramatica sumelor de termeni oarecare la care ajunsesem mai sus, astfel:

% arith.pl
expr_test(add(T, R)) --> term(T), rest(R).
rest(E) --> [+], expr_test(E) | [].
term(A) --> [A].

?- expr_test(T, [a,+,b,+,c], []).
T = add(a, add(b, add(c, _G2721))) ; % a observa că termenii sunt grupaţi la dreapta!
false.

?- expr_test(T, [a], []).
T = add(a, _G2691).

Invocările "?-" redate evidenţiază defectele acestei reformulări grăbite; fiindcă am montat add(T, R) chiar în startul procesului recursiv, urmează că ultimul termen al sumei date ca intrare (în speţă 'c', respectiv 'a') va fi înlocuit cu add(c, _G2721), unde _G... reprezintă o variabilă internă care n-a putut fi instanţiată (ea s-ar instanţia prin add pentru următorul termen, care lipseşte).

Parametrul - unic - add(T, R) din clauza expr_test serveşte pentru construcţia recursivă a arborelui sintactic; dar add(T, R) presupune doi "operanzi": unul pentru subarborele deja construit, iar celălalt pentru termenul următor (dacă mai există unul). În principiu, variabila finală neinstanţiată _G... putea fi evitată dacă prevedeam un al doilea argument - sub forma expr_test(add(T, R), Next) - pe care să se instanţieze termenul următor (dacă există).

Construcţia arborelui sintactic - spre dreapta, respectiv spre stânga

În funcţie de locul în care vom monta un asemenea parametru (într-o clauză sau alta, în partea stângă a ei, sau în partea dreaptă) vom putea şi să "alterăm" convenabil arborele sintactic - pentru a-l obţine sub forma add(add(a, b), c) (cu grupare la stânga, ca în cazul "left-recursion"), în loc de - cum am constatat deja mai sus - add(a, add(b, c)).

Având în vedere defectele evidenţiate mai sus pentru expr_test, putem reformula astfel:

% arith.pl
expr_right(E)        --> term_r(T), rest_r(T, E).
rest_r(T, pow(T, E)) --> [^], expr_right(E).
rest_r(End, End)     --> [].  % "condiţia de oprire" (a recursivităţii)
term_r(A)            --> [A].

?- expr_right(T, [a,^,b,^,c], []), !.
T = pow(a, pow(b, c)).  % a^b^c = a^(b^c) (asociere la dreapta)

Am înlocuit "expr_test" cu "expr_right"; am văzut deja că termenii vor fi asociaţi la dreapta - încât "pow" este mai adecvat decât "add". Am montat constructorul pow(T, E) în clauza rest_r (şi nu în cea de start, cum făcusem - defectuos - în "expr_test") şi anume, după parametrul T destinat termenului "următor" (astfel, arborele sintactic va fi construit spre dreapta).

Alternativa rest_r(End, End) --> [] va fi folosită atunci când se va ajunge la ultimul termen al expresiei, încheind construcţia recursivă a arborelui: End va fi unificat cu arborele sintactic construit pe primul parametru, devenind la revenirea din rest_r valoarea finală a argumentului lui expr_right (a trasa execuţia, de exemplu pentru expresia a^b).

Această "reformulare" moşteneşte însă un defect de formulare a recursivităţii: din rest_r se apelează expr_right care după ce capturează încă un termen, apelează înnapoi rest_r. Este cu siguranţă mai eficient, ca rest_r să captureze ea însăşi termenul care urmează după operatorul pe care l-a depistat şi apoi să se reapeleze (fără a mai intermedia prin apelul lui "expr_right"):

expr_right(E)          --> term_r(T1), rest_r(T1, E).
rest_r(T1, pow(T1, E)) --> [^], term_r(T2), rest_r(T2, E). % a^b^c = pow(a, pow(b, c))
rest_r(End, End)       --> [].
term_r(A)              --> [A].

Când rest_r(T1, _Pow1) întâlneşte '^' şi apoi încă un termen T2 - se reapelează rest_r, care în urma unificărilor produse între parametri devine un apel de forma rest_r(T2, _Pow2)); pe linia ascendentă a apelurilor, variabilele interne _Pow "ţin locul" arborelui sintactic curent - aceştia urmând să fie instanţiaţi în ordine inversă apelărilor (la revenirea din apel). De exemplu, pentru a^b^c întâi va fi instanţiată _Pow3 = c (când lanţul de apeluri atinge ultimul termen), apoi (la "Exit"-ul următor) se va instanţia _Pow2 = pow(b, c) şi în final, _Pow1 = pow(a, pow(b, c)) (a trasa eventual, execuţia!).

În cazul operatorilor care asociază termenii spre stânga, arborele sintactic curent trebuie instanţiat imediat ce se va fi capturat termenul din dreapta operandului - deci pe linia ascendentă a apelurilor recursive (astfel încât noul termen să poată fi "alipit" arborelui parţial existent). Pentru aceasta, constructorul add(T1, T2) trebuie montat ca parametru în partea dreaptă a clauzei recursive:

expr_left(E)  --> term_l(T1), rest_l(T1, E).
rest_l(T1, E) --> [+], term_l(T2), rest_l(add(T1, T2), E). % a+b+c = add(add(a, b), c)
rest_l(E, E)  --> [].
term_l(A)     --> [A].

Când expr_left recunoaşte termenul T1 - îl pasează clauzei rest_l; aici - dacă după T1 urmează un termen T2, atunci se construieşte arborele add(T1, T2) şi acesta este pasat mai departe ca primul parametru al următoarei reapelări rest_l. Astfel, primul argument din expr_l este mereu arborele curent construit; clauza "de oprire" rest_l(E, E) va unifica E cu arborele sintactic rezultat în primul argument şi acesta va fi "returnat" apelului de start expr_left(E).

O gramatică finală, pentru expresiile algebrice uzuale

Prolog investighează clauzele "de sus în jos"; aceasta ne scuteşte de vreo explicitare de priorităţi - formulăm definiţiile corespunzătoare în ordinea priorităţilor. Pentru +, -, *, / avem deja şablonul expr_left, iar pentru ^ vom folosi modelul expr_right. În Prolog, variabilele sunt locale clauzei (E dintr-o clauză nu are de-a face cu E din alte clauze) - încât putem evita să nuanţăm mai mult decât trebuie, denumirile folosite pentru variabile:

% arith_dcg.pl
expr(E)       --> term(T), rest_1(T, E).
rest_1(E0, E) --> [+], term(T), rest_1(add(E0, T), E).
rest_1(E0, E) --> [-], term(T), rest_1(sub(E0, T), E).
rest_1(E, E)  --> [].

term(E)       --> power(P), rest_2(P, E).
rest_2(E0, E) --> [*], power(P), rest_2(mul(E0, P), E).
rest_2(E0, E) --> [/], power(P), rest_2(dvi(E0, P), E).
rest_2(E, E)  --> [].

power(E)               --> factor(F), rest_3(F, E).
rest_3(E0, pow(E0, E)) --> [^], factor(P1), rest_3(P1, E).
rest_3(E, E)           --> [].

factor(A) --> [A].
factor(E) --> ['('], expr(E), [')'].

Ca exemplu, pentru 20-(14/5*2)^3 (al cărei arbore sintactic l-am şi desenat anterior) obţinem:

?- expr(T, [20,-,'(',14,/,5,*,2,')',^,3], []).
T = sub(20, pow(mul(dvi(14, 5), 2), 3)).

Pentru a formula această gramatică "finală" - după atâtea demersuri iterative anterioare - n-am făcut altceva, decât să rescriem - aproape copiind - expr_left şi expr_right (pentru primele patru operaţii şi respectiv pentru "pow").

Dar astfel (însăilând copii ale celor două şabloane) avem în mod inerent o derulare care ar putea provoca îndoieli: expr(E) implică term(T) şi apoi rest_1 recursiv; dar clauza term(E) invocată astfel, implică power(P) şi apoi rest_2 recursiv; mai departe, clauza power(E) implică factor(F) şi apoi rest_3 recursiv - iar după aceasta, urmează revenirile succesive.

Abia ajungând la clauza factor, are loc instanţierea lui F şi după aceasta, se intră în rest_3; dacă după "factorul" capturat în F nu urmează '^' - se iese din rest_3, încheind power(E) cu unificarea E = F (transmiţând mai departe, "factorul" depistat); la revenirea în term(E), se unifică P = F şi se lansează rest_2. Presupunând că nu urmează nici '*', nici '/' - se iese din rest_2, transmiţând mai departe F; abia acum, revenind în expr - se unifică T = F şi apoi se intră în rest_1, rezolvând situaţiile rămase ('+', '-', sau "termen final").

Dar nu-i cazul să încercăm să îmbunătăţim formularea gramaticii de mai sus; în fond, "defectul" tocmai semnalat este comun mecanismelor care angajează funcţii mutual recursive, iar pe de altă parte, gramatica la care am ajuns aici nici nu este una nouă - figurând în forme apropiate printre exemplificările uzuale ("clasice") de gramatici LL(1).

În principiu, soluţionarea acestui "defect" trebuie să aibă în vedere tocmai ceea ce gramatica de mai sus a figurat în mod implicit (prin ordinea clauzelor): priorităţile operatorilor. Dacă odată cu fiecare termen s-ar "captura" şi operatorul care îi urmează, atunci s-ar putea decide deodată - pe baza priorităţii acestuia (eventual, în raport cu a operatorului precedent) - care clauză trebuie aplicată mai departe; dar aceasta ţine mai degrabă de implementare (de care Prolog ne-a scutit, prin handler-ul său de DCG), decât de formularea gramaticii respective.