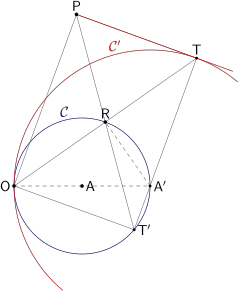Fixăm punctele $O$ şi $A$ şi fie $\mathcal{C}$ cercul de centru $A$ cu raza $AO$; notăm cu $A'$ simetricul lui $O$ faţă de $A$.

Fie $R$ un punct oarecare pe $\mathcal{C}$ şi fie $T$ simetricul lui $O$ faţă de $R$, iar $T'$ cealaltă intersecţie cu $\mathcal{C}$ a dreptei $TA'$; fie $P$ simetricul lui $T'$ faţă de $R$.

Ce curbe descriu $T$ şi $P$, când $R$ parcurge cercul $\mathcal{C}$?

Din construcţia indicată – care simplifică pe cea redată în [1], unde vizam "puterile" punctelor – rezultă uşor că $OT'TP$ este un dreptunghi: $T'R$ este mediană în triunghiul dreptunghic $OT'T$ (avem $\measuredangle OT'A'=90^\circ$, fiindcă $OA'$ este diametru în $\mathcal{C}$), deci $T'R=OR$ – prin urmare, diagonalele $T'P$ şi $OT$ sunt egale.

În plus, $TA'=2\,OA$ (fiindcă $AR$ este linie mijlocie în $\Delta OA'T$, iar $AR=AO$); deci locul lui $T$ (când $R$ parcurge $\mathcal{C}$) este cercul $\mathcal{C}'$ de centru $A'$ şi rază $A'O=2\,OA$.

Obs. $\mathcal{C}'$ provine din $\mathcal{C}$ prin omotetia de centru $O$ şi raport 2, fiindcă pentru oricare puncte corespondente $T$ şi $R$ avem $\vec{OT}=2\,\vec{OR}$.

Fiindcă $PT\perp TA'$ şi $A'$ este centrul cercului $\mathcal{C}'$, rezultă că $PT$ este tangentă în $T$ la $\mathcal{C}'$; altfel spus, $P$ este proiecţia lui $O$ pe o tangentă a cercului $\mathcal{C}'$.

Obs. Această caracterizare a punctelor $P$ ignoră de fapt construcţia făcută mai sus, în care plecam de la punctul $R$ mobil pe cercul $\mathcal{C}$. Dreptunghiul construit plecând de la $R$ mai sus, poate fi considerat ca fiind cel format de tangenta şi normala într-un acelaşi punct $T$ al curbei $\mathcal{C}'$ – presupunând însă că această curbă este dată – şi de perpendicularele pe acestea din punctul fixat $O$ şi problemele s-ar pune astfel: ce curbă descrie vârful $P$ când $T$ parcurge curba dată $\mathcal{C}'$? respectiv, ce curbă descrie centrul $R$ al dreptunghiului, când $T$ parcurge $\mathcal{C}'$? În cazul de aici, când $\mathcal{C}'$ este un cerc, rezultă că locul lui $R$ este cercul $\mathcal{C}$ omotetic (faţă de polul $O$, cu raportul de omotetie 0.5) cercului dat $\mathcal{C}'$, iar locul lui $P$ – o cardioidă, cum vom stabili mai jos – poate fi construit punctual cum am arătat mai sus (plecând de la punctele $R$ ale cercului iniţial $\mathcal{C}$).

Pentru a găsi ecuaţia curbei descrise de $P$, să reperăm punctele faţă de originea $O(0,0)$ şi punctul unitar $A(1,0)$.

Cercul $\mathcal{C}'$ (cu centrul $A'(2,0)$ şi raza $OA'=2$) are ecuaţia $(x-2)^2+y^2=4$, care se mai scrie $x^2+y^2-4x=0$. Derivând în raport cu $x$, $2x+2yy'-4=0$, găsim panta tangentei în $T(\alpha,\beta)\in\mathcal{C}'$: $m=\left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_{x=\alpha}=\frac{2-\alpha}{\beta}$.

Deci ecuaţia tangentei la $\mathcal{C}'$ în $T(\alpha,\beta)$ este $y-\beta=\frac{2-\alpha}{\beta}(x-\alpha)$, care (ţinând cont imediat că avem $\alpha^2+\beta^2=4\alpha$) se reduce la $$\alpha(x-2)+\beta y=2x\quad\quad\quad(1)$$

Perpendiculara din $O(0,0)$ pe tangenta la $\mathcal{C}'$ în $T(\alpha,\beta)$ are ecuaţia $y=-\frac{1}{m}x$, sau $$\alpha y-\beta x=2y\quad\quad\quad(2)$$

Rezolvăm (cu "regula lui Cramer") sistemul de ecuaţii (1), (2) şi obţinem $\alpha=\frac{2(x^2+y^2)}{x^2+y^2-2x}$ şi $\beta=\frac{4y}{x^2+y^2-2x}$; înlocuind în $\alpha^2+\beta^2-4\alpha=0$, găsim ecuaţia locului intersecţiei $P$ a tangentei în $T$ la $\mathcal{C}'$ cu perpendiculara din $O$ pe aceasta: $\small (x^2+y^2)^2+4y^2-2(x^2+y^2)(x^2+y^2-2x)=0$, sau într-o formă echivalentă $$(x^2+y^2-2x)^2-4(x^2+y^2)=0\quad\quad\quad(3)$$ şi recunoaştem că aceasta reprezintă cardioida cu nodul $O(0,0)$ şi vârful $A'(2,0)$
(în [3] am speculat "diferenţa de pătrate", obţinând o parametrizare cu radical a ecuaţiei (3) prin care am "redus" studiul acesteia la semi-cardioida superioară).

Precizăm că locul proiecţiilor unui punct pe tangentele unei curbe date formează podara acesteia faţă de punctul respectiv; ceea ce am demonstrat mai sus revine la această proprietate binecunoscută: podara unui cerc faţă de un punct al său este o cardioidă. Podarele cercurilor (omotetice faţă de punctul comun $O$) $\mathcal{C}'$ şi $\mathcal{C}$ sunt cardioide omotetice, cu nodul comun $O$.

În [2] am arătat o proprietate mai generală: $\mathcal{C}^{n+1}$ este podara faţă de $O$ a lui $\mathcal{C}^n$ (unde $\mathcal{C}^n$ desemna "puterea a n-a" a cercului de diametru 1 care trece prin $O$); în particular, podara cardioidei ($\mathcal{C}^2$) faţă de nodul său este o sextică Cayley ($\mathcal{C}^3$).