Reluăm ideea conturată în [1] şi [2]: modulând valorile unei expresii de coordonate, atribuim fiecărui punct câte un indice de culoare; periodicitatea resturilor va atrage repetarea anumitor şabloane de repartizare a culorilor, producând eventual "decoraţiuni artistice" ale pânzei. În [3] este reflectată o rafinare a acestei idei: valorile sunt modulate de două ori, vizând eventual, proprietăţi ale gamei de valori ale expresiei şi apoi, ţinând seama de mărimea gamei de culori.

Pentru [3] m-am cam lăsat "furat" de un experiment liniar: angajam valori aleatorii pentru cele două valori de modulare succesivă, aşteptând de fiecare dată să văd dacă obţin ceva care să-mi placă; dar cu o schemă aşa de simplă - nu-i de mirare că un timp, lucrurile au rămas tulburi… N-ar merita să mai redăm schema respectivă - totuşi, cam de aici am plecat:

hypcol <- function(W=250, param=NULL) {
  G <- W / 2
  if(is.null(param)) {
    c1 <- sample(1:656, 1)  # indicele de bază pentru culori
    c2 <- sample((c1+1):657, 1)  # maxim pentru indicele culorii
    mod <- sample(2:256, 1)  # pentru reducerea valorilor iniţiale
    by <- sample(1:mod, 1)  # reduce la un indice de culoare
  } else {
    c1 = param[1]; c2 = param[2]
    mod = param[3]; by = param[4]
  }
  pal <- colors()[seq(c1, c2, by=by)]  # paleta de culori
  raster <- as.raster(outer(1:W, 1:W, function(u, v) 
                            pal[1 + ((u - G)^2 - (v - G)^2) %% mod %% by]))
  plot(raster)  # plot(raster, interpolate=FALSE)
  print(c(c1, c2, mod, by))
}

De exemplu, cu hypcol(p = c(195, 333, 40, 34), W = 80) se obţine una dintre imaginile redate deja în [3]. Se vede că iniţial am considerat pentru "mod" o valoare aleasă arbitrar (în intervalul 2:256 - gândindu-mă tot la culori), în loc de a o lega cumva de gama valorilor expresiei. Iar faptul că am încorporat "totul" (generarea valorilor, stabilirea culorilor), denaturează calitatea de "funcţie" a secvenţei de mai sus (şi "ascunde" lucrurile).

Pentru rescrierea funcţiei hypcol() ne ghidăm după observaţiile expuse mai jos, vizând (dar nu chiar separat) secvenţierea culorilor şi numărul acestora, alegerea coordonatelor şi a expresiilor, precum şi scalarea valorilor.

Secvenţierea culorilor, cu sau fără interpolare

Parametrul "c2" ne-a părut la un anumit moment, inutil ("maximul indicelui de culoare" fiind în fond, lungimea vectorului returnat de colors()); pare suficient să precizăm de la ce indice plecăm şi cu ce pas "by" urmează să se avanseze în vectorul de culori. Are sens parametrizarea culorilor (într-un mod sau altul), cum se poate vedea (pe primele două imagini) modificând numai "c2":

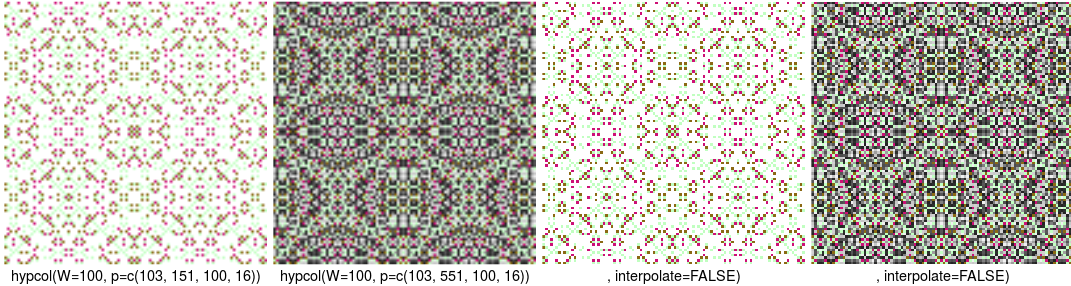
Pentru prima imagine s-au folosit patru culori:

> colors()[seq(103, 151, by=16)]
[1] "darkseagreen1" "deeppink3" "firebrick2" "goldenrod4"

iar pentru a doua, (551 - 103) / 16 = 28 culori. Cu alte cuvinte, aceleaşi valori din intervalul de numere întregi [0, 99] (rezultate prin reducerea valorilor iniţiale faţă de "mod" = 100) au fost clasificate în patru şi apoi în 28 clase (asociind apoi câte o culoare, fiecărei clase de valori). Dar pe imagine, clasele respective nu sunt neapărat strict separate: plot .raster() - adaptarea funcţiei generice plot() pentru obiecte de tip 'raster' - invocă în final funcţia image(), iar aceasta (în mod implicit) "netezeşte" culorile (cu posibilă diminuare a clarităţii imaginii, sau a contrastului - dar în general, cu efect mai plăcut decât în absenţa interpolării).

Pentru a treia şi a patra imagine, am folosit apelul plot(raster, interpolate = FALSE) (încât image() nu a mai netezit culorile, reprezentând clasele de valori prin dreptunghiuri distincte, colorate corespunzător); desigur, nu am folosit direct acest apel: am adăugat funcţiei hypcol() argumentul "..." şi am înlocuit linia "plot(raster)" prin "plot(raster, ...)" - asigurând transmiterea parametrului "interpolate" (către funcţia plot()) de la nivelul hypcol().

Să observăm acum că într-adevăr, "c2" este inutil (şi doar îngreunează lucrul, ceea ce iniţial era mascat de faptul că valoarea lui era generată aleatoriu - cât timp indicam în apelul hypcol() cel mult parametrul "W"); este mai firesc (dar şi cu mai multe şanse de a nimeri o gamă convenabilă de culori) să considerăm un parametru de distanţare între culori care să nu mai depindă de "by" - fie "ecart": atunci, cum "by" ne dă în fond numărul de culori, avem şi c2 = c1 + ecart * by.

Dar cel mai firesc este să externalizăm stabilirea culorilor. Rămâne de văzut şi dacă vom găsi o modalitate mai convenabilă pentru a constitui "paleta de culori", decât cea bazată pe colors() (cum avem iniţial în hypcol()).

Coordonate, expresii, filtrarea valorilor

În experimentul următor imităm construcţia funcţiei iniţiale hypcol():

1
2
3
4
5
6
7

FUN <- function(u, v) (u-G)*(v-G)  # 'G' va fi evaluat la momentul apelului (din context) 
pal <- c("sienna4")  # "paleta de culori" (aici, cu lungimea mai mică decât 'by')
mod <- 25; by <- 5
W <- 50; G <- W / 2  # centrul imaginii este punctul (G, G)
raster <- outer(1:W, 1:W, function(u, v) 
                pal[1 + FUN(u,v) %% mod %% by])  # '%%' păstrează semnul divizorului
plot(as.raster(raster), interpolate=FALSE)

În hypcol() am considerat din start o singură expresie (diferenţa pătratelor); dar putem viza diverse alte expresii de coordonate şi s-ar cuveni să externalizăm definiţia funcţiei respective. Astfel, în secvenţa de mai sus funcţia FUN() (care va furniza produsul coordonatelor) este definită în exteriorul operaţiei de creare a obiectului "raster" (precizăm că R permite "lazzy evaluation", încât definiţia variabilei 'G' din corpul funcţiei poate fi amânată).

Am ales astfel parametrii (în liniile 2, 3 şi 4), încât să putem sesiza uşor anumite aspecte. Dacă măcar una dintre coordonate (u sau v) este multiplu de 5, atunci FUN(u, v) %% 25 %% 5 este 0 - încât (prin liniile 5 şi 6) punctului respectiv îi va fi asociată culoarea pal[1], definită în linia 2.
În schimb, de exemplu pentru (u, v) = (6, 32) avem: FUN(6, 32) = (6-25)*(32-25) = -133; fiindcă operatorul "modulo" (desemnat prin "%%") păstrează semnul divizorului (nu al deîmpărţitului, ca în C, javaScript, etc.) - obţinem (-133) %% 25 %% 5 = 17  %% 5 = 2, încât punctului (6, 32) îi va fi asociată "culoarea" pal[3], adică valoarea "NA" (nu am definit decât valoarea pal[1], iar pentru valorile care "nu există" R prevede valoarea specială "NA").

Funcţia image() ignoră valorile "NA" (sau - depinzând de dispozitivul grafic - le interpretează drept culoare complet transparentă); prin urmare, în cazul de faţă vor fi colorate (cu valoarea pal[1]) numai punctele de abscisă sau ordonată multiplu de 5 (prima imagine), respectiv (pe a doua şi a treia) cele pentru care rezultatul reducerii succesive faţă de 25 şi 3 este 0:

Pe prima imagine culoarea este modificată, fiindcă am adăugat o grilă - pentru a observa valorile din 5 în 5 - colorată cu albastru. Mărind W - deci numărul de puncte luate în calcul - modelul "principal" se repetă (parţial) de mai multe ori, iar imaginea devine mai clară (a treia imagine, faţă de a doua; pentru acestea, am redefinit FUN(u, v) = abs(u*v) şi by = 3).

Deducem această metodă de filtrare a punctelor: considerând un număr de culori Q mai mic decât "by" - vor fi ignorate acele puncte pentru care expresia de coordonate folosită dă valori a căror reducere (întâi faţă de "mod" şi apoi faţă de "by") ajung să fie mai mari decât Q (iar în exemplificarea de mai sus, avem Q = 1).

Mai observăm pe aceste imagini că pixelii de la marginile inferioară şi din dreapta sunt "în plus" (strică aspectul general de simetrie); am uitat de faptul că pixelii sunt totdeauna indexaţi de la 0, când - în linia 5 din secvenţa de cod de mai sus - am generat coordonatele începând cu 1. Ar fi trebuit să folosim fie 0 : W, fie 1 : (W-1); dar cel mai bine am folosi (-W) : W - caz în care centrul imaginii este chiar originea axelor, încât nu mai este necesară variabila "G" (v. liniile 4 şi 1).

Sintetizări (şi ilustrări)

Alegând "W" mai mare sau mai mic, obţinem mai multe sau mai puţine repetări ale unui aceluiaşi model (eventual, cu claritate mai bună, respectiv mai slabă a imaginii); dar variind valoarea după care clasificăm valorile iniţiale ("mod", în cadrul funcţiei hypcol()) găsim decoraţiuni care uneori diferă mult ca structură (şi uneori, obţinem doar decoraţiuni "fade", sau uniforme).

S-ar pune problema de a defini valoarea (orientativă) faţă de care modulăm valorile iniţiale, încât decoraţiunea rezultată să sintetizeze "cât mai bine" (armonios, interesant, etc.) modelele vizuale posibile pentru valorile respective (şi să nu mai depindă aşa de mult de "W"). Măcar pentru unele categorii de expresii, am găsit experimental că o asemenea valoare ar rezulta raportând la "W" media aritmetică a unora dintre valorile iniţiale; uneori, nu obţinem nimic interesant folosind chiar valoarea determinată astfel, dar lucrurile se pot "rezolva" ulterior prin angajarea directă a unei valori apropiate acesteia (mai mică sau mai mare cu 1 sau 2).

Generarea aleatorie (dacă aşa dorim) a valorilor unora dintre parametri se poate face "din exterior" - încât, în baza observaţiilor de mai sus, am rescrie hypcol() astfel:

decorate <- function(W=100, FUN, colors, v_mod=NULL, p_mod=NULL, ...) {
  if(is.null(p_mod))  # decorează cu măcar două culori
    p_mod <- ifelse((lc <- length(colors)) == 1, 2, lc)
  if(is.null(v_mod)) {  # valoarea faţă de care sintetizăm valorile iniţiale
    v_mod <- round(mean(outer(W, 0:W, FUN)) / W)
    if(v_mod %%2 == 0) v_mod <- v_mod + 1  # (pare preferabil un modul impar)
  }  
  raster <- as.raster(outer(-W:W, -W:W, function(u, v) 
                            colors[1 + FUN(u, v) %% v_mod %% p_mod]))
  plot(raster, ...) # primeşte eventual (din linia de apel), 'interpolate=FALSE'
  mtext(paste0(deparse(substitute(FUN)), ", (%", v_mod, " %", p_mod, "), ", W), 
        side=1, line=0.25, cex=0.9)  # comunică parametrii de bază ai decoraţiunii
}

Arătăm o situaţie în care întâi apelăm fără nici un parametru de reducere, iar apoi reapelăm specificând o valoare "v_mod" micşorată faţă de "modulul orientativ" (= 73) furnizat iniţial:

> decorate(function(u, v) u^2-v^2, col=c("black"), W=110)  # modulul orientativ: 73
> decorate(function(u, v) u^2-v^2, col=c("sienna4"), W=110, v=71)  # micşorând modulul

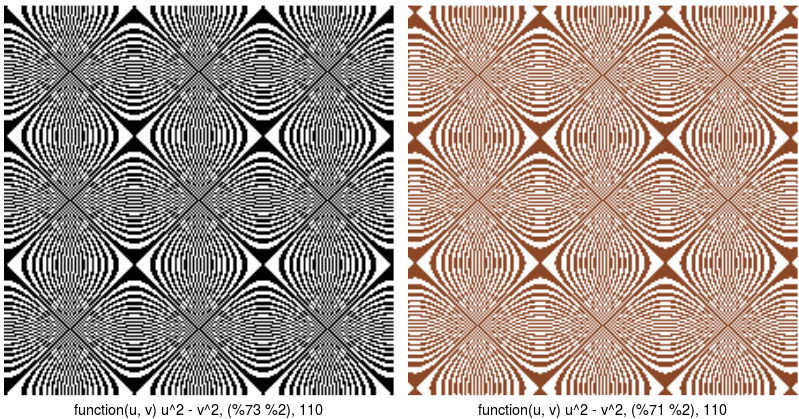
Micşorând "v_mod" (în cazul de faţă, de la 73 la 71), decoraţiunea se comprimă (zonele marginale sunt mai extinse la a doua imagine, faţă de prima); poate rezulta astfel o anumită diminuare a asperităţilor iniţiale (mai ales dacă folosim o culoare potrivită). Modelul circular din centru (care se repetă şi în celelalte "centre") este mai fin conturat în a doua imagine; în prima imagine (dar nu şi în a doua) avem iluzia neplăcută a unor dungi (trei orizontale şi trei mai groase, verticale).

Pentru următoarele două decoraţiuni am folosit aceleaşi valori de reducere ca mai sus, dar am indicat trei culori, iar pentru a doua am schimbat funcţia din u² - v² în abs(u² - v²):

Mai jos, folosim valori diferite pentru "W" (16 şi respectiv, 110), dar un acelaşi set de 8 culori (în loc de trei, ca deasupra; a compara a doua imagine de mai jos cu cea de-a doua de deasupra) şi o aceeaşi funcţie (valorile de modulare fiind cele setate în mod implicit de decorate()):

Pentru prima imagine, am adăugat în linia de apel şi "interpolate = FALSE" (încât pixelii sunt redaţi prin dreptunghiuri distincte); pentru a o "gusta" mai bine, ea trebuie privită de la distanţă.

Următoarele două decoraţiuni reprezintă aceleaşi valori iniţiale (furnizate prin abs(u*v)), reduse prin valoarea orientativă (25) calculată în decorate() (rezultând modelul "de bază") şi respectiv printr-una mult mai mică (15), folosind două şi respectiv 8 culori (cu şi respectiv, fără interpolare):

În zona centrală a imaginii din dreapta putem recunoaşte (totuşi) modelul "de bază" (din prima imagine); înjumătăţirea valorii orientative (de la 25, la 15) a determinat (desigur, împreună cu proprietăţile de simetrie ale funcţiei implicate) producerea iluziei vizuale a curbării dreptelor orizontale şi verticale, în jurul zonei centrale (privind de aproape, imaginea respectivă; iar privind mai de departe - iluzia unor romburi concentrice).

Pentru următoarea ilustrare am folosit o funcţie logaritmică, round(100*log(u^2 + v^2); iniţial, pentru "valoarea orientativă" furnizată de decorate() (17 pentru W=50, 19 pentru W=40, etc.) imaginea era cumva "incoerentă" şi am ales până la urmă "v_mod" = 6 (şi W = 40):

Pentru prima imagine, am ales 5 nuanţe de gri, obţinute prin gray.colors(5)); pentru a doua - am ales cele trei culori ceva mai sofisticat: col = c("gray35", "gray35", "white"), colorând la fel valorile 0 şi 1 (iniţial, cu numai două culori distincte, imaginea ni s-a părut mai puţin "atractivă").

Un calcul statistic complementar ne-a arătat că (pentru modele şi submodele grafice simetrice, precum în toate imaginile redate mai sus) valoarea "v_mod" trebuie aleasă în aşa fel încât culorile să fie distribuite uniform (înălţimile barelor unei histograme a valorilor reduse faţă de "v_mod" să fie cât mai apropiate), sau după o schemă "bi-uniformă" (bare de o aceeaşi înălţime, intercalate cu bare de o altă aceeaşi înălţime, astfel încât histograma acestora să fie - principial vorbind - simetrică faţă de centru). Apoi, obţinerea de imagini "atractive" depinde de colorarea barelor histogramei la care tocmai ne-am referit; în scopul mascării unor asperităţi este de luat în seamă ideea de a "comasa" anumite bare, indicând pentru ele o aceeaşi culoare (cum am procedat în cazul ultimei imagini de mai sus).

Mai semnalăm că schimbarea ordinii culorilor (ceilalţi parametri fiind identici) produce imagini destul de diferite una faţă de cealaltă:

Pentru prima imagine am folosit col=c("#B8C3C5", "#C16DC8", "#B6D978"), iar pentru a doua am mutat prima culoare la sfârşitul vectorului celor trei culori.