Pânzele drumurilor hamiltoniene pe graful calului 5x5
În [1] am obţinut fişierul "knight5_.txt", conţinând toate drumurile hamiltoniene ale grafului calului pe tabla de şah 5x5 - dar într-un format informativ devenit inutil:
1. Drum hamiltonian: 1 8 5 14 25 18 21 12 3 10 19 22 11 2 9 20 23 16 7 4 15 24 13 6 17 2. Drum hamiltonian: 1 8 5 14 25 18 21 12 3 10 19 22 11 2 9 20 23 16 7 4 15 24 17 6 13 .................... 304. Drum hamiltonian: 1 12 9 2 13 20 23 16 7 4 15 24 17 6 3 10 19 22 11 8 5 14 25 18 21 1: 304 # în total avem 304 drumuri din vârful 0 1. Drum hamiltonian: 3 6 17 24 15 4 7 16 23 20 13 10 19 22 11 2 9 18 21 12 1 8 5 14 25 .................... 56. Drum hamiltonian: 3 10 13 6 17 24 15 4 7 16 23 20 9 2 11 22 19 8 5 14 25 18 21 12 1 3: 56 # 56 drumuri care pleacă din vârful 2 ....................
Putem elimina liniile "informative" din acest fişier folosind perl:
vb@vb:~/KNIGHT$ perl -ne 'print unless /hamilt|\d+:/' < knight5_.txt > knight5.txt
Liniile care nu conţin "hamilt" şi care nu conţin o secvenţă de cifre urmată de ":" - vor fi scrise rând pe rând în fişierul final "knight5.txt". Mai general, perl -n -e 'COD' file.txt execută (-e) secvenţa COD pentru fiecare linie (-n) din fişierul indicat.
Ne-a rezultat astfel fişierul "knight5.txt", conţinând exact 1728 de linii - reprezentând fiecare câte un drum hamiltonian al grafului calului de şah pe tabla 5x5.
Am lămurit în [1] că un astfel de drum startează obligatoriu de pe un câmp de aceeaşi culoare (sau paritate) cu a colţurilor tablei. Este necesar deasemenea, ca măcar unul dintre capetele drumului să fie un colţ - altfel, ar trebui să se treacă de două ori printr-un acelaşi câmp.
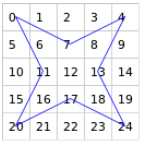 Într-adevăr, să presupunem un drum hamiltonian D care nu începe dintr-un colţ şi nu se încheie într-un colţ. La un moment dat, D va intra în colţul 0 prin arcul (7, 0) şi va ieşi prin arcul (0, 11)
Într-adevăr, să presupunem un drum hamiltonian D care nu începe dintr-un colţ şi nu se încheie într-un colţ. La un moment dat, D va intra în colţul 0 prin arcul (7, 0) şi va ieşi prin arcul (0, 11) (sau invers); în colţul 20, D nu va putea intra prin arcul (17, 20), fiindcă ieşirea (20, 11) ar însemna trecerea a doua oară prin câmpul 11. Deci pentru D este obligatoriu (începând din 7, 11, 17 sau 13) traseul 7 - 0 - 11 - 20 - 17 - 24 - 13 - 4; pentru a continua către nodul final (diferit de colţuri), D ar trebui să iasă din colţul 4 - dar aceasta înseamnă trecerea a doua oară prin unul dintre câmpurile 7 sau 13.
Fiecare drum care pleacă dintr-un colţ şi se încheie în nodul N (colţ sau nu), se va regăsi în ordine inversă între drumurile care pleacă din nodul N; am vrea să păstrăm din fişierul "knight5.txt" numai cele 1728/2 = 864 de drumuri "directe", renunţând la duplicatele inversate ale acestora. Preferăm să realizăm aceasta folosind Python:
# is_same(L1, L2) == True <=> listele L1 şi L2 sunt identice (ca elemente şi ca ordine) is_same = lambda L1, L2: \ len(L1)==len(L2) and len(L1)==sum([1 for i,j in zip(L1, L2) if i==j]) koni = open("knight5.txt") # conţine cele 1728 de drumuri hamiltoniene hams = [] # va înregistra drumurile "directe", nu şi inversele acestora for drum in koni: # transformă linia curentă din fişier în listă de întregi (nodurile drumului) L1 = [int(node) for node in drum.strip().split()] # inversează drumul curent L1 L2 = [node for node in reversed(L1)] # adaugă drumul în ham[] numai dacă inversul lui n-a fost deja înscris found = False for ham in hams: if is_same(L2, ham): found = True break if not found: hams.append(L1) print hams # va scrie drumurile unul după altul, pe o singură linie
zip(L1, L2) împerechează elementele de aceleaşi ranguri din cele două liste, iar apoi sum([1 for i,j in zip(L1, L2) if i==j] contorizează perechile de valori egale - încât funcţia anonimă is_same(L1, L2) testează dacă listele respective (în speţă, un drum hamiltonian şi inversul său) coincid.
Executăm scriptul redat mai sus, redirectând ieşirea către un fişier:
vb@vb:~/KNIGHT$ python knight5.py > knight5_.txt
Lista vizată în script prin "hams", a fost înscrisă în fişierul "knight5_.txt" pe o singură linie: [[1, 8, 5, ..., 13, 6, 17], [1, ..., 13], ..., [23, ..., 25]]; preferăm să dispunem drumurile respective "unul sub altul" şi să eliminăm toate spaţiile:
vb@vb:~/KNIGHT$ perl -pe 's/ \[/\n\[/g' knight5_.txt > knight5_.js vb@vb:~/KNIGHT$ perl -pi -e 's/ //g' knight5_.js
Prima comandă înlocuieşte " [" cu "\n[" şi forţează "print" (opţiunea -p), iar a doua elimină toate spaţiile din fişierul rezultat (scriind în acelaşi (opţiunea -i) fişier).
În final, knight5_.js conţine cele 864 de drumuri hamiltoniene "directe", câte unul pe linie. Dacă prefixăm lista respectivă cu var paths = (şi adăugăm la sfârşit ";"), obţinem un fişier javaScript, definind variabila "paths" ca un Array() având ca elemente tablouri de numere. Vizăm acest fişier şi angajăm tabloul javaScript conţinut paths[], în următoarea pagină HTML:
- Fig. 1 -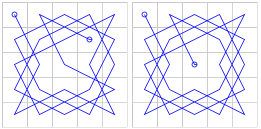
<html> <head> <meta charset="utf-8"> <title>Knight</title> <script src="../static/js/jquery-1.7.2.min.js"></script> <script src="knight.js"></script> <script src="knight5_.js"></script> </head> <body> <div id="kn5"></div> <script> $(function() { for(var i=0, n=paths.length; i < n; ++i) { set_canvas(5, "kn5", paths[i], i); } }); </script> </body> </html>
După ce browser-ul (Firefox, de exemplu) va încărca acest fişier HTML, va executa <script>-ul de la sfârşit; acesta preia paths[i] (pentru i=0..paths.length-1) şi îl transmite funcţiei set_canvas(), care ar avea sarcina de a adăuga în diviziunea "kn5" un element <canvas> conţinând imaginea grafică a drumului hamiltonian respectiv.
Bineînţeles că definim set_canvas() ceva mai general: pentru orice dimensiune de tablă şi pentru orice traseu transmis - dar… nu ne străduim mai mult pentru a organiza lucrurile (de exemplu sub forma unui widget jQuery - cum am mai făcut, în Modelarea tablei şi jocului de şah).
function set_canvas(n, id_dest, path, rang) { var field = 25; // dimensiunea câmpului var size = n*field; canvas = document.createElement('canvas'); canvas.setAttribute('width', size+5); canvas.setAttribute('height', size+5); canvas.setAttribute('title', rang); // rangul în path[] al drumului de pe pânză ctx = canvas.getContext("2d"); ctx.strokeStyle = "rgb(200, 200, 200)"; ctx.lineWidth = 0.5; for(i=0; i <= n; i++) { // trasează liniile care marchează câmpurile var dx = field*i+0.5; ctx.moveTo(dx, 0); ctx.lineTo(dx, size); ctx.moveTo(0, dx); ctx.lineTo(size, dx); ctx.stroke(); } var dest = document.getElementById(id_dest); dest.appendChild(canvas); ctx.beginPath(); var start = path[0] - 1; // câmpul de start al drumului var x = parseInt(start / n); var y = start % n; ctx.arc(field*(x+0.5), field*(y+0.5), 2.5, 0, Math.PI * 2); ctx.moveTo(field*(x+0.5), field*(y+0.5)); ctx.strokeStyle = "rgb(0, 0, 255)"; ctx.lineWidth = 0.75; for(var i=1; i < path.length; ++i) { // trasează muchiile drumului var next = path[i] - 1; x = parseInt(next / n); y = next % n; ctx.lineTo(field*(x+0.5), field*(y+0.5)); } ctx.arc(field*(x+0.5), field*(y+0.5), 2.5, 0, Math.PI * 2); ctx.stroke(); }
În Fig. 1 (vezi mai sus), am redat primele două dintre cele 864 de "pânze" rezultate prin execuţia de către browser a scriptului de mai sus. Ar fi de remarcat anumite aspecte de simetrie, între pânzele corespunzătoare drumurilor care unesc colţuri opuse; redăm trei perechi de pânze "simetrice":

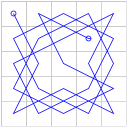
Ar fi de observat deasemenea, că aplicând rotaţii de 90° putem regăsi dintr-o "pânză" dată, alte trei pânze. Pentru un exemplu, reproducem iarăşi pe prima dintre cele 864 de pânze; fiecare click pe imaginea alăturată o va roti cu 90°, conducând la o alta dintre pânzele obţinute prin scriptul de mai sus.
(pentru a roti imaginea, am implicat plugin-ul Rotate)
Desigur, ar fi acum de "amendat" valoarea 864 - pentru a ţine seama şi de coincidenţele datorate simetriei sau rotaţiei aplicate drumurilor respective…
vezi Cărţile mele (de programare)