Continuăm încercarea de a sintetiza într-un program de "creaţie grafică", funcţiile de plotare din R; faţă de [1], evităm explicitarea vreunor vectori de coordonate (cum aveam în corpul funcţiei plotart()) şi angajăm mai multe modalităţi (specifice limbajului R) de furnizare a datelor. Acum, prototipul (sau "semnătura") funcţiei finale arată astfel:

plotart <- function(x, y = NULL,  # structuri de date cu 2 sau 4 vectori de coordonate
                    p = NULL, q = NULL,  # vectori de combinat cu vectorii de coordonate
                    drv = NULL,  # 'png', 'svg' (implicit: ecranul)
                    tip = 1,  # puncte, linii sau segmente (plot(), lines() sau segments())
                    asp = 1,  # "aspect-ratio"
                    grade = NULL,  # (opţional) funcţie de colorare, pentru smoothScatter()
                    ...  # parametri grafici de pasat funcţiilor implicate 
                   )  

Dacă 'y' rămâne "NULL" - nefiind explicitat în linia de apel a funcţiei - atunci structura de date corespunzătoare lui 'x' va trebui să fie sau un vector de numere complexe (caz în care 'x' şi 'y' vor prelua părţile reale şi respectiv imaginare, ale acestuia), sau o matrice (ori "data.frame") cu două sau patru coloane reale, sau o listă cu două sau patru componente; altfel, 'x' şi 'y' vor putea fi specificaţi (direct sau prin expresii de calcul) ca vectori (eventual de clasă "complex").

Dacă vor rezulta patru coloane şi 'p' va fi explicitat ca vector în linia de apel, atunci urmează să se constituie un vector de abscise şi unul de ordonate combinând oricare valoare din 'p' şi oricare valoare din 'q' cu oricare valoare din câte două coloane (şi însumând corespunzător, rezultatele).

În cazul a două coloane, 'tip' va trebui să fie 1 sau 2 - pentru a plota "puncte" cu abscisele şi ordonatele respective, respectiv pentru a trasa linii între puncte consecutive; dacă sunt patru coloane, atunci 'tip' va trebui să fie 3 - pentru trasarea segmentelor de capete indicate de câte două dintre aceste coloane.

'asp' nu poate fi lăsat în seama argumentului "...", pentru că valoarea respectivă intervine în calculul dimensiunilor ferestrei grafice specifice cazului când 'drv' este "png" (sau "svg").

Extragerea vectorilor de coordonate

Mai toate funcţiile grafice asumă că datele sunt transmise în structuri precum cele vizate mai sus şi apelează funcţia R xy.coords() pentru a extrage vectorii de abscise şi ordonate necesari (vezi eventual R source code); dar aici, avem de rezolvat şi situaţii ignorate de xy.coords() (cazul când nu numai 'x' este "complex", dar şi 'y'; sau cazul combinării coloanelor de date cu parametrii 'p' şi 'q') - şi ca urmare este necesară o funcţie proprie pentru extragerea coordonatelor:

my_coords <- function(x, y = NULL, p = NULL, q = NULL) {
    tip <- TRUE  # două coloane / patru coloane de date
    if(is.null(y)) {  # apelul plotart() nu a furnizat şi pe 'y'
        if(is.complex(x)) {
            y <- Im(x)  # ordinea extragerii contează! (întâi 'y', apoi 'x')
            x <- Re(x)
        } else if(is.matrix(x) || is.data.frame(x) || is.list(x)) {
                    if(is.list(x)) {
                        x <- matrix(unlist(x), ncol=length(x))  # transformă în matrice
                    } else x <- data.matrix(x)
                    if(ncol(x) == 2) {
                        y <- x[, 2]  # ordinea extragerii contează!
                        x <- x[, 1]
                    } else if(ncol(x) == 4) {
                               x0 <- x[, 1]; y0 <- x[, 2]
                               x1 <- x[, 3]; y1 <- x[, 4]
                               tip <- FALSE
                           } else stop("need two or four columns")
               } else stop("only allowed matrix|data.frame|list")
    } else {  # plotart() a furnizat şi 'x' şi 'y' (vectori reali sau complecşi)
          if(length(x) != length(y)) stop("lengths differ")
          if(is.complex(x) && is.complex(y)) {
              x0 <- Re(x); y0 <- Im(x)
              x1 <- Re(y); y1 <- Im(y)
              tip <- FALSE
          }
   }
   if(tip) return(list(x, y))
   if(is.null(p)) return(list(x0, y0, x1, y1))
   pair(x0, y0, x1, y1, p, q)
}

Funcţia pair() (al cărei rezultat este returnat în ultimul caz, mai sus) foloseşte expand.grid() pentru a împerechea în toate modurile posibile valorile unui vector ('x0', 'x1', etc.) cu valorile lui 'p' (şi respectiv 'q'), furnizând în final noi vectori (de forma x0*p + x1*q):

pair <- function(x0, y0, x1, y1, p, q=NULL) {
    if(is.null(q)) q <- 1 - p
    p1 <- expand.grid(p, x0)  # produsul cartezian al valorilor vectorilor
    p2 <- expand.grid(q, x1)
    x <- p1$Var1 * p1$Var2 + p2$Var1 * p2$Var2  # p*x0 + q*x1 (∀ x0, x1, p, q values)
    p1 <- expand.grid(p, y0)
    p2 <- expand.grid(q, y1)
    y <- p1$Var1 * p1$Var2 + p2$Var1 * p2$Var2  # p*y0 + q*y1
    list(x, y)
}

Redăm un singur test - pentru un caz simplu (vector "complex", de lungime 1) în care putem folosi şi xy.coords() (iar mai jos, vor apărea în mod implicit diverse alte cazuri):

> my_coords(1 + 1i*3)  # numărul complex 1 + 3i
[[1]]
[1] 1  # abscisa x = 1
[[2]]
[1] 3  # ordonata y = 3

> xy.coords(1 + 1i*3)
$x
[1] 1
$y
[1] 3
$xlab
[1] "Re()"
$ylab
[1] "Im()"

Neavând nevoie să reprezentăm axele, am ignorat numele de componente şi etichetele cerute sau furnizate funcţiilor grafice de către xy.coords().

Degradarea culorii de fundal

Prin parametrul 'grade' din prototipul redat la început al funcţiei

smoothScatter() calculează după o anumită schemă "densitatea" datelor primite ca parametru şi o reliefează grafic printr-o anumită treptare (de lungime 256) a culorilor; această "gradare" este de fapt o funcţie precum colorRampPalette(), care primeşte ca argument o secvenţă de culori şi returnează o funcţie care produce un vector cu lungimea indicată la apel, conţinând culori care interpolează secvenţa respectivă.

Următorul experiment (pe seama coordonatelor din [2] §4) arată întâi că este importantă ordinea în care sunt indicate culorile pe baza cărora este raportată grafic densitatea punctelor:

u <- seq(0, 2*pi, pi/120)  # 2*120+1 = 241 valori echidistante din [0, 2π]
lxy <- my_coords(as.complex(3*sin(u)^3 - 0.75i*cos(4*u)),
                 as.complex(1.5*sin(u)^5 - 0.5i*cos(3*u)),
                 p = c(0.1, 0.3, 0.7))  # implică pair() (rezultă câte 3*241=723 valori)
names(lxy) <- c("x", "y")  # denumeşte componentele, cum aşteaptă smoothScatter()
opar <- par(mfrow = c(1, 2), mar = c(0,0,0,0), xaxt = "n", yaxt = "n")  # două panouri
grade <- colorRampPalette(c("black", "white"), alpha = TRUE)
smoothScatter(lxy, colramp = grade, asp = 0.9)  # pe primul panou
grade <- colorRampPalette(c("white", "black"), alpha = TRUE)  # Ordinea culorilor contează!
smoothScatter(lxy, colramp = grade, asp = 0.9, col = NA)  # pe al doilea panou
par(opar)  # reconstituie parametrii grafici iniţiali (un singur panou, cu margini şi axe)

În primul caz (panoul din stânga), densitatea creşte de la "black" (pentru zone libere) spre "white" (zone dense), iar în al doilea - invers (ar fi de observat că în primul caz am omis setarea "col = NA", încât au fost reprezentate şi punctele "izolate" - acelea care prin setarea implicită pentru "lăţimea de bandă" au ajuns să fie ignorate la calculul densităţii bidimensionale). Deci în cazurile când am vrea să evidenţiem (prin contrast) zonele dense, culorile pe baza cărora să se constituie fundalul trebuie indicate începând cu nuanţa cea mai închisă (ca în primul caz).

Dar să observăm că am obţinut cam prea mult faţă de ce ne-ar putea fi de folos: voiam numai o "culoare de fundal", gradată potrivit densităţii punctelor - nu o variantă "mai groasă" a însăşi imaginii care s-ar obţine prin plotarea acestora. Încercăm să corectăm printr-o idee foarte simplă: reducem la jumătate - dar printr-o selecţie aleatoare - numărul de puncte luate în considerare pentru calculul densităţii; pentru aceasta, aplicăm prin lapply() funcţia sample() componentelor listei 'lxy' din secvenţa precedentă:

nxy <- lapply(lxy, 
              function(lc) sample(lc, 0.5*length(lc)))  # 50% dintre valori (aleatoriu)
grade <- colorRampPalette(c("black", "white"), alpha=TRUE)
smoothScatter(nxy, colramp=grade, asp=0.9, col=NA)  # pe primul panou
grade <- colorRampPalette(c("white", "black"), alpha=TRUE)
smoothScatter(nxy, colramp=grade, asp=0.9, col=NA)  # pe al doilea panou

Fireşte, dacă am fi mărit în prealabil numărul de valori din vectorul 'u' (micşorând pasul din definiţia acestuia de la 'pi/120' la 'pi/720', de exemplu), atunci am fi obţinut un fundal mai uniform (ceea ce este desigur de dorit); de altfel, pentru un număr mic de puncte (ca în acest experiment) - nu are sens să mai asociem un fundal imaginii respective.

Rescrierea funcţiei plotart()

Întâi (vezi textul funcţiei, mai jos) apelăm my_coords() pentru datele sau expresiile primite şi în funcţie de lungimea listei obţinute se determină limitele axelor (corectând eventual şi valoarea parametrului "tip" - nu poate fi 3 pentru cazul a doi vectori de coordonate şi nu poate fi diferit de 3 dacă este vorba de coordonatele capetelor de segmente).

Dacă s-a specificat 'drv="pgn"' sau 'drv="svg"' - calculăm dimensiuni potrivite imaginii: alegem ca lăţime 100*dx (unde 'dx' este diferenţa dintre abscisa maximă şi cea minimă) şi dacă este cazul, incrementăm cu câte 30 de pixeli până ce avem o lăţime de cel puţin 450 pixeli; apoi calculăm şi înălţimea ţinând cont de raportul 'dy / dx' şi de valoarea parametrului "asp". Pentru dimensiunile rezultate astfel - şi pentru un nume de fişier generat în funcţie de ziua, ora şi minutul la care s-a apelat funcţia - se construieşte "fereastra grafică", invocând png(), sau svglite::svglite().

Mai departe, anulăm zonele şi însemnele implicite (specifice graficelor statistice) - marginile (prin parametrul 'mar'), bordura (prin 'bty="n"') şi axele (având grijă în final, să restabilim parametrii).

Dacă s-a optat pentru constituirea unui fundal (indicând în parametrul "grade" o funcţie de colorare după densitate) - selectăm aleatoriu 50% dintre puncte şi invocăm smoothScatter() pentru acestea (mediind între abscisele şi respectiv ordonatele capetelor segmentelor, în cazul în care "tip" este 3).

Apoi, în funcţie de valoarea parametrului "tip" se apelează plot(), sau lines(), sau segments() - transmiţând (prin argumentul "...") parametrii grafici specifici (sugeraţi în liniile de comentariu aferente, din programul care urmează).

plotart <- function(x, y=NULL, p=NULL, q=NULL, 
                    drv=NULL, tip=1, asp=1, grade=NULL, ...) {
    xy <- my_coords(x, y, p, q)
    if(length(xy) == 2) {
        if(tip == 3) tip <- 2  # stop("tip=3 needs four coordinates")
        x <- xy[[1]]; y <- xy[[2]]
        xlt <- range(x); ylt <- range(y)  # limitele axelor de coordonate
    } else {
        if(tip != 3) tip <- 3  # stop("here we have four coordinates")
        x0 <- xy[[1]]; y0 <- xy[[2]]
        x1 <- xy[[3]]; y1 <- xy[[4]]
        xlt <- range(c(x0, x1))
        ylt <- range(c(y0, y1))
    }
    if(!is.null(drv)) {
        dx <- diff(xlt); dy <- diff(ylt)  # dimensiunile reale ale ferestrei grafice
        wd <- dx * 100  # calculează dimensiunile ferestrei grafice, în pixeli
        while(wd < 450) wd <- wd + 30
        hg <- wd * dy / dx * asp # + 16
        filename <- paste("images/CA", format(Sys.time(), "%d%H%M"), ".", drv, sep="")
        switch(drv,
            png = png(filename = filename, units="px", 
                      width = wd, height = hg, bg="transparent"),  #, res=300),
            svg = svglite::svglite(file = filename, 
                                   width = wd/72, height = hg/72, bg="transparent")
        ) 
    }
    opar <- par(mar=c(0, 0, 0, 0), bty="n", xaxt="n", yaxt="n")
    if(!is.null(grade)) {
        if(tip != 1) {
            if(tip == 2) {
                sz <- length(x) / 2
                xs <- sample(x, sz)  # selectează aleatoriu 50% dintre puncte
                ys <- sample(y, sz)
            } else {
                sz <- length(x0) / 2
                xs <- sample(0.5*(x0 + x1), sz) 
                ys <- sample(0.5*(y0 + y1), sz)
            }
        smoothScatter(xs, ys, xlim=xlt, ylim=ylt, col=NA, asp=asp, colramp=grade)
        }
     } else {
        plot.new()
        plot.window(xlim = xlt, ylim = ylt, asp = asp, ...)
    }
    switch(tip,
        plot(x, y, ...),  # cex=3.5, col="gray7", pch=21 | type="o", lwd=0.4, lty="dotted"
        lines(x, y, ...),  # lwd=0.6, col="gray3"
        segments(x0, y0, x1, y1, ...)  # col="gray3", lwd=1, lty=1 
    )
    par(opar)  # restabileşte parametrii grafici impliciţi
    if(!is.null(drv)) dev.off()
}

Să exemplificăm întâi folosind lista 'lxy' din experimentul de mai sus (considerând fundalul creat acolo şi apoi, unul mai potrivit):

opar <- par(mfrow = c(2, 1))  # o coloană a două panouri
plotart(lxy, tip=3, asp=0.9, lwd=1.15, 
        grade=colorRampPalette(c("black", "white"), alpha=TRUE))  # pe primul panou
plotart(lxy, tip=3, asp=0.9, lwd=1.15,
        grade=colorRampPalette(c("lightblue", "snow", "white"), alpha=TRUE))  # al II-lea
par(opar)

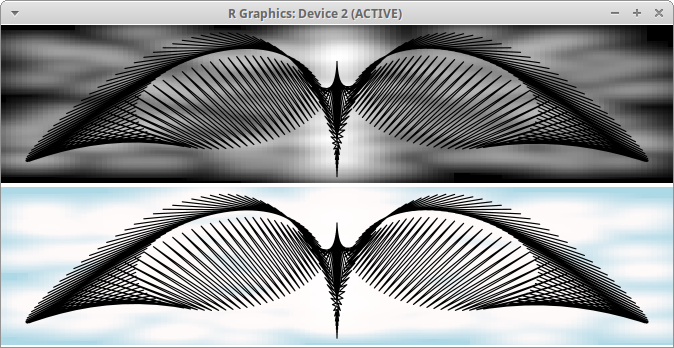
Ar fi de observat că petele de culoare ale fundalului vor varia (ca poziţie şi ca întindere) de la o execuţie la alta a apelului respectiv - dat fiind că acele 50% dintre valori care sunt transmise funcţiei smoothScatter() sunt alese în mod aleatoriu, dintre valorile vectorilor de coordonate.

Am constatat că este uşor de reprodus (sau de imitat) prin programul redat mai sus, imagini obţinute prin vechiul program - trebuie doar să adaptăm parametrii apelurilor - încât nu ne mai ocupăm aici de alte exemplificări (dar am adăugat deja pe computer_art_R câteva noi imagini, împreună cu lista corespunzătoare de parametri).