$\sqrt{z(z+1)}$ transformă cercul unitate într-o curbă care seamănă cu o cardioidă.
TeX şi MetaPost, pe o trisectoare Pascal
Fişier LaTeX care integrează cod MetaPost (necesitând ca '\write18' să fie activată) pentru a arăta (şi documenta) într-o aceeaşi figură construcţii principial diferite (generând "toate" punctele, respectiv folosind operatorul "path_join" pentru anumite 6 puncte) ale unei trisectoare Pascal.
Metafont pentru trisectoarea lui Pascal
Dacă limbajul respectiv prevede un anumit mecanism de interpolare, atunci pentru construcţia graficului ar putea fi suficientă indicarea doar a câtorva puncte (şi direcţionări). Construim cu MetaFont trisectoarea lui Pascal, indicând doar anumite 6 puncte (şi direcţiile tangentelor).
Metafont pentru lemniscata lui Bernoulli (partea a cincea)

"simplu.log" sintetizează exemplar activitatea compilatorului şi dezvăluie intuiţiei logica lucrurilor.
Metafont pentru lemniscata lui Bernoulli (partea a patra)
Cum vom crea "cadrul tangent" lemniscatei lui Bernoulli 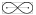 ?
?
Cu alte cuvinte - cum construim (folosind MF) un dreptunghi, ştiind centrul şi un vârf ?
Ilustrăm caracterul descriptiv al limbajului MetaFont şi modul specific de a concepe o "funcţie".
vezi Cărţile mele (de programare)