Creaţie grafică (croşetare) folosind R



imitaţie după
A Bird in Flight (November 2014)
Experimente de grafică folosind R
Prezentăm şi speculăm prin două exerciţii (nelegate de statistică), parametrii grafici de bază din R.
Grafică statistică şi grafică "artistică", pentru două variabile



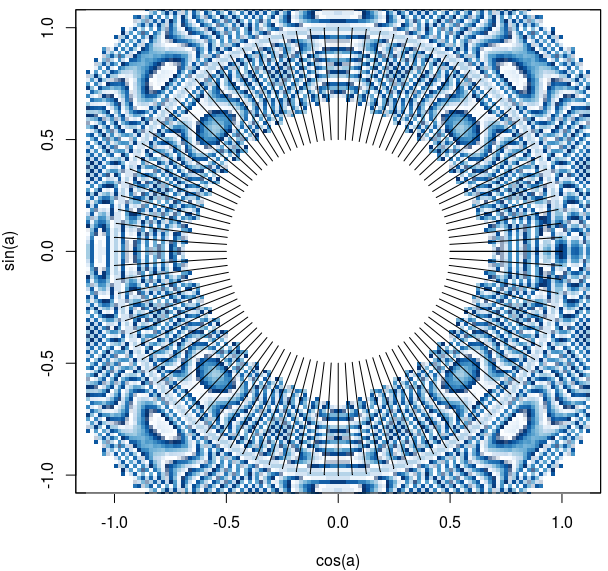
Generăm un anumit număr de puncte având drept coordonate expresii simple de sin() şi cos(); cu funcţia smoothScatter() obţinem o estimare de densitate a punctelor, reliefată printr-o anumită gradare a culorilor de acoperire a unor zone; apoi, plotăm segmentele corespunzătoare perechilor de puncte.
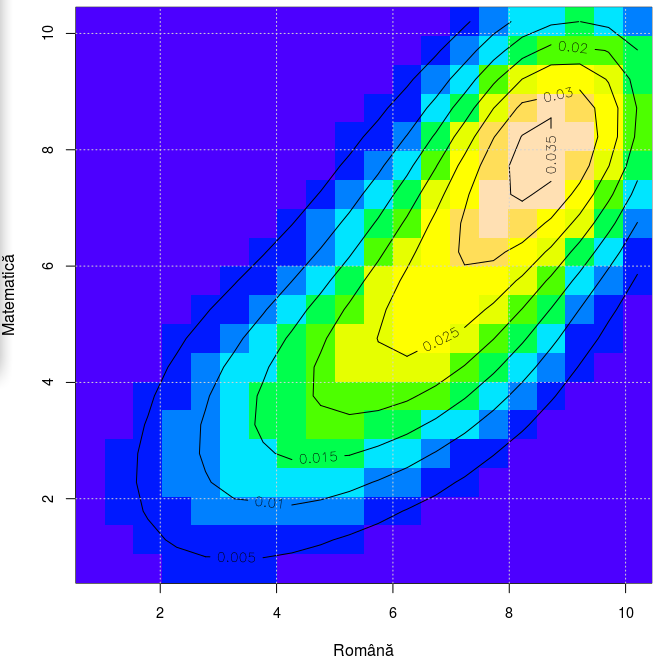
Ideea este de a corela o histogramă verticală (pentru notele de la "Română") cu una orizontală ("Matematică"). ...dedesubtul diagonalei duse prin colţul (0,0) avem mult mai multă culoare decât deasupra, însemnând că pentru majoritatea elevilor notele la "Română" sunt mai mari decât cele de la "Matematică".
Studiul datelor evaluării naţionale din 2016 (folosind R)

Studiul datelor examenului de bacalaureat din 2016 (folosind R)
unde găsim că normalitatea este o iluzie şi este chiar greu de simulat!
vezi Cărţile mele (de programare)